Le Retournement de la Sphère
8 décembre 2004
page 4
La version de Bernard Morin
Pour télécharger la version pdf de l'article de 1979 de B. Morin et J.P.Petit, paru dans Pour la Science
Le retournement de la sphère ( 2,8 Mo )
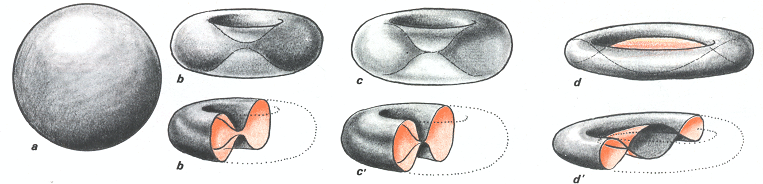
On va partir d'une sphère qui présente sa face grise vers l'extérieur et sa face rose à l'intérieur. En b et c on amène ses pôles en contact. Puis les nappes s'interpénètrent selon un "catastrophe du coude". Il y a création d'une courbe fermée d'auto-intersection. En bas et à droite trois demi-coupes permettent de mieux de sendre compte de la configuration obtenue. A ce stade la sphère ressemble à une sorte de "canot pneumatique" circulaire, avec un "boudin" et un "plancher" à double paroi.

Première étape : une "catastrophe du coude". Création d'une courbe fermée d'auto-intersection
Deuxième opération : nouvelle catastrophe du coude, création d'une seconde courbe fermée.
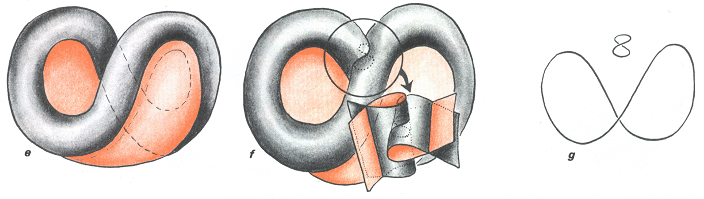
Seconde création d'une courbe fermée d'auto-intersection.
Pour ce faire le "canot pneumatique" s'est plié, avec un mouvement de vrillage, ce qui a permis d'amener deux partie du "boudin", diamétralement opposées, en contact. L'image suivante est le résultat de deux catastrophes conduisant à la création de "tranches de mandarine".
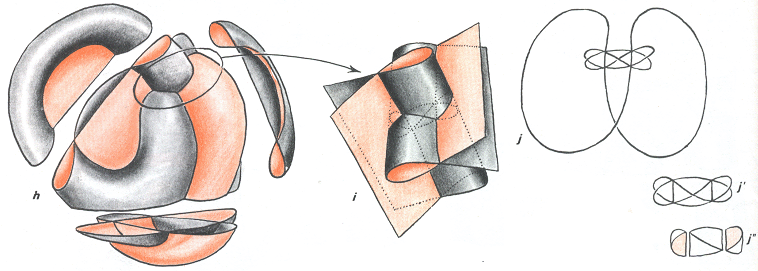
Après création de deux "tranches de mandarine"
A gauche on a opéré des coupes dans le modèle. Au centre la façon dont les deux cylindres dont, localement, la section affecte la forme de la lettre grecque "gamma" se sont interpénétrés. On se rappelle que la catastrophe de création de "tranches de mandarines" s'opérait en coupant une "bûche" avec deux plans formant un dièdre. Chacune des structures cylindriques dont la section est en "gamma" comporte à la fois la section arrondie et le dièdre. Regardez avec attention la figure i. En j on a dessiné l'ensemble d'auto-intersection. La portion de courbe fermée la plus grande provient de la première "catastrophe du coude" qui avait transformé la sphère en "canot pneumatique". Après création des deux tranches de mandarines on obtient un ensemble plus complexe dont j' est un sous-ensemble. En j" on voit que cette structure peut être comparée à l'assemblage de deux "tranches de mandarine" sur deux arêtes d'un tétraèdre, non adjacentes.
Tout cela sera un jour beaucoup plus simple à appréhender quand j'aurai pu produire des animations. Cela ne me pose aucun problème technique a priori. C'est une simple question de temps. Rares sont les gens qui peuvent non seulement voir dans l'espace, c'est à dire lire ce codage utilisant des lignes, des pointillés, des couleurs, des ombres et des reflets mais aussi enchaîner dans leur tête des transformations en imaginant le mouvement suggéré. J'espère avoir un jour le temps de faire toutes ces choses. Remarquons au passage qu'on pourrait utiliser des modèles polyédriques, comme je l'ai fait pour montrer comment on peut transformer une Crosscap en Surface de Boy. Là est l'avenir. Mais ces modèles, il faut les inventer. On trouvera plus loin la version polyédrique optimisée du modèle central de cette transformation imaginée par Bernard Morin ( rappelons que c'est un aveugle !), avec la façon de la construire soi-même à partir d'un découpage.
Pourquoi n'ai-je pas poussé ces choses plus loin ? Je dirais : faute de "débouchés". Il n'y a pas de revues de mathématiques qui acceptent de publier de tels travaux. Nous avons pu le faire en 1975-78 à travers quelques notes aux Comptes Rendus de l'Académie des Sciences de Paris, qui n'ont sans doute pas du être lues par grand'monde. Mais c'était parce que l'académicien André Lichnérowicz s'intéressait personnellement à ces travaux. Il est aujourd'hui décédé. Comme ces travaux avaient complètement abouti dès 1975 il aurait été souhaitable de produire un film d'animation à partir de mes dessins. Ayant travaillé dans le dessin animé j'étais tout à fait capable de coordonner une telle entreprise. Mais il fut impossible de trouver un financement au Cnrs et c'est finalement le mathématicien américain Nelson Max qui, s'inspirant de maquettes construites par son collègue Charles Pugh (de cette même version du retournement de la sphère), et utilisant un puissant ordinateur parvint à produire le premier un film. Mais ce n'est ni la première, ni la dernière fois que des Français, ne recevant aucun écho à leurs efforts se font ainsi coiffer au poteau par des collègues étrangers mieux organisés et mieux soutenus.
Passons à la troisième phase, la plus difficile à saisir.
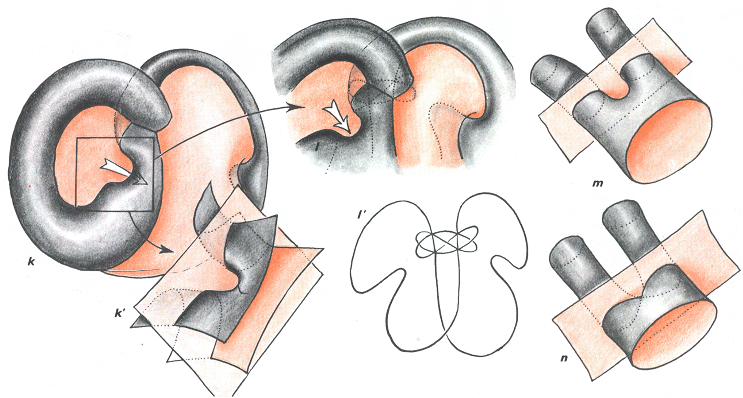
Préparation de deux catastrophes "du pantalon"
Dans la figure k on distingue bien les deux bouts de "jambes de pantalon", dont le détail figure dans un avant-plan k' . La flèche blanche indique le passage "dans l'entre-jambes". Cette transformation est vraiment difficile à appréhender. J'ai ajouté le dessin m pour tenter d'être mieux compris. En l j'ai représenté à l'aide de pointillés la courbe d'auto-intersection, qui figure dans son ensemble en l' . Un passage (celui emprunté par la flèche blanche) va se refermer. Ce mouvement de fermeture va avec la montée d'une partie de la courbe d'intersection, en deus endroits. Ces bouts de courbe vont venir au contact, chacune, sur l'une des lignes appartenant à des "transches de mandarine". Quand le contact s'effectuera, la chirurgie s'opérera. La difficulté vient du fait que lorsqu'on a vu les quatre catastrophes élémentaires, dans la page précédente, il faut être capable de les transposer sous toutes les angles, en se dévissant les vertèbres du cou, au besoin. En n on a figuré le moment critique où la chirurgie s'opère (la "situation médiane" de la transformation) et où le mode de raccordement des bouts de courbe va être modifié. On sait que cette catastrophe "du pantalon" ferme un passage et en ouvre un autre. Le passage initial est figuré par la flèche blanche. Mais il en existe un autre qu'on apercevrait sous le même angle en faisant tourner le modèle de 180° sur lui-même autour d'un axe vertical. Ces flèches n'en forment qu'une. Avant que ces catastrophes ne s'opèrent il est encore possible de circuler dans ce "canot pneumatique replié". Quand ces catastrophes auront fait leur effet ce passage ne sera plus possible. Par contre deux autres passages se seront créés. Mais où, quelles parties de l'espace sont-elles concernées ? Ces passages mettront l'intérieur des tranches de mandarines en communication avec l'extérieur. En l', ces tranches de mandarines, vous les voyez. Passons à l'étape suivante.
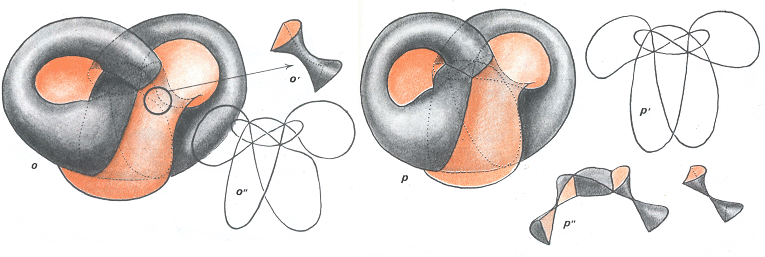
Fermeture du passage. Vers une double situation critique
En o on a représenté les deux catastrophe "du pantalon" à deux stades différents. L'un des passages en complètement fermé. On est en situation critique, juste avant ques les arcs de courbe voient leur mode de raccordement changer. A droite (détail sur la figure o' ) le passage est seulement en train de se refermer. Ainsi l'allure de la courbe d'auto-intersection o" est-elle différente à droite et à gauche. Sur les figures p, p' et p" la criticité (situation "médiane" de la transformation) est atteinte des deux côtés. Sur la planche ci-après les chirurgies ont fait leur effet. Les tubes qu'on voyait s'amorcer sur la figure p", mettant en communication les "tranches de mandarine" avec l'extérieur sont maintenant formés :
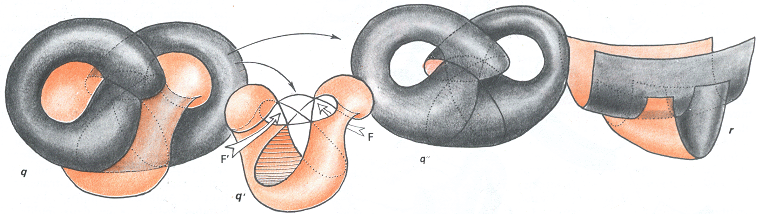
Les deux "catastrophes du pantalon" on fait leur effet. Les passages ( flèches blanches ) sont ouverts.
Les choses vont maintenant se poursuivre en travaillant sur la partie inférieure du modèle, dont le détail en indiqué en r . Regardons cette portion de surface avec attention. Nous voyons deux portions de cylindres paraboliques qui se croisent, en étant dirigé selon deux directions orthogonales. Il existe un passage à la partie inférieure de r qui fait face au lecteur. Nous allons envisager de faire glisser ces deux cylindres l'un par rapport à l'autre. Ceci aurait alors pour effet de fermer ce passage et d'en ouvrir un autre courant selon la direction perpendiculaire ( "de droite à gauche" ). Nous reconnaissons ici une nouvelle "catastrophe du pantalon". Si ce glissment vertical de ces portions de cylindres paraboliques s'opère, nous déboucherons de nouveau sur une situation critique, avec changement du mode de raccordement des nappes. Mais en fait, par simple souci d'économie, nous stopperons le "process" à la criticité, en "situation médiane" lorsque le passage dirigé vers le lecteur se refermera et que le passage situé dans la direction perpendiculaire ne sera pas encore ouvert. Faisons cela.
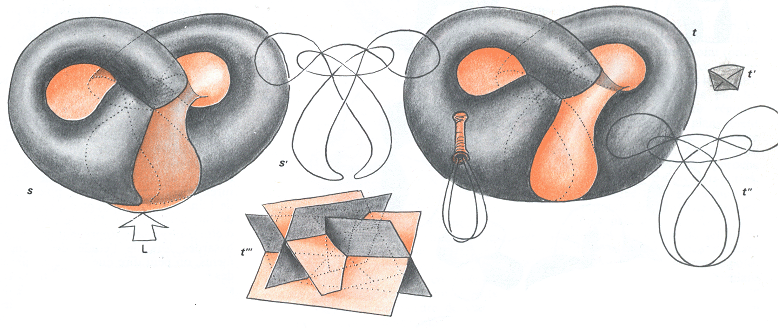
Nouvelle catastrophe du pantalon, amorcée en L, stoppée à droite, à la criticité.
On va opérer en L une "pression" sur le cylindre qui présente sa couleur rose vers l'extérieur et le faire monter. En c' on voit l'impact qu'a ce mouvement sur l'ensemble d'auto-intersection : les arcs de courbe commencent à se rapprocher. Quand la criticité sera atteinte cette partie de l'ensemble ressemblera à "un fouet pour batte les oeufs", représenté sur la figure. Figures de droite, t , t', t" : la criticité est atteinte, c'est à dire "l'instant médian de la catastrophe". En t" l'allure de l'ensemble d'auto-intesection dont la partie inférieure s'identifie à celle de notre fouet à battre les oeufs. La figure t' représente le petit volume tétraèdrique. En t''' on a figuré le croisement des quatre nappes.
Allez avaler une aspirine.
Dans cette version du retournement de la sphère toutes les transformations, les catastrophes devraient être amenées à leur terme. Mais on va bloquer celle que nous venons d'évoquer dans sa configuration médiane, "critique". Nous allons ensuite amorcer une catastrophe que nous n'avons pas encore utilisée : celle qui inverse un tétraèdre. Mais là encore nous nous arrêterons à la situation "médiane", quand ce tétraèdre est réduit à un point. Allons-y !
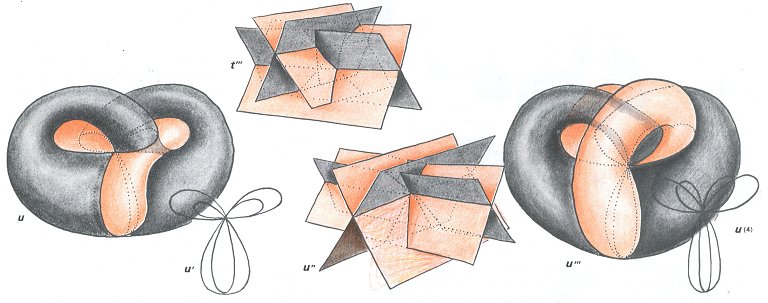
Dernière catastrophe, bloquée à son stade médian : quand le tétraèdres est réduit à un point quadruple Q
En t ''' une évocation de la configuration des quatre nappes dont l'ensemble d'auto-intersection contient un volume affectant la forme d'un tétraèdre. En u" ce tétraèdre a été réduit à un point ( quadruple, puisqu'il y a quatre nappes qui se croisent ). A gauche le "modèle à quatre oreilles de Morin" est constitué. En avant plan l'ensemble d'auto-intersection avec, en bas, le "fouet pour battre les oeufs" et en haut quatre ganse évoquant des "oreilles de lapin". En déformant un peu la surface, mais sans opérer de nouvelles catastrophes on débouche à droite sur le modèle central à quatre oreilles de Morin. Celui ci a une symétrie d'ordre quatre. Si on effectuait une rotation de 90° autour de son axe de symétrie vertical, on obtiendrait le même dessin, mais avec des couleurs échanges. Le gris devient rose et vice-versa. Alors nous pouvons dire que le travail est terminé. En effet, si nous voulions dessiner l'homotopie complète il suffirait, à l'aide d'une animation, de faire tourner de 90° ce modèle central. Puis nous pourrions reprendre tous les dessins que nous avons faits, à rebours, avec des couleurs échangées. A bout du compte nous obtiendrions un plongement de la sphère où celle-ci présente sa couleur rose à l'extérieur. Mais les mathématiques sont une école de paresse, ou d'économie, selon le regard que l'on porte à la chose. Dans la mesure où le travail nous a amené à un objet présentant cette symétrie d'ordre quatre nous pouvons en rester là en disant que l'opération a été menée à bien.
Dans la planche suivante je me suis efforcé de décrire ce modèle central ouvert de Morin avec le maximum de détails. Il existe un modèle avec "oreilles fermées", que j'ai décrit dans une autre nos à l'Académie, mais je vous en ferai grâce.
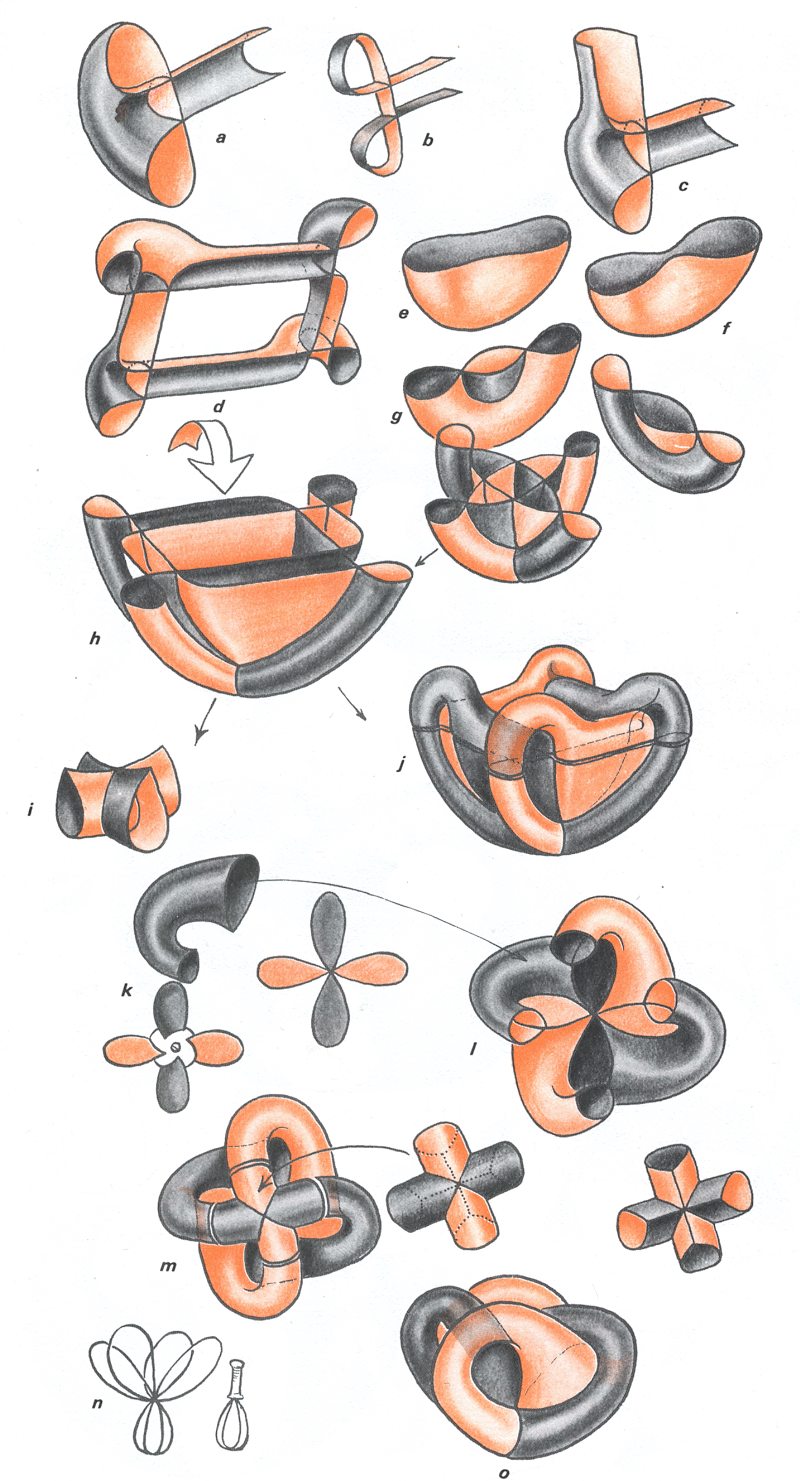
Description détaillée du modèle central de Morin, à quatre oreilles
Par la suite j'ai trouvé une représentation polyédrique du modèl central à quatre oreilles. En fait un tel modèle n'a ni "haut", ni "bas". Pour des commodités de dessin et d'animation ( j'ai obtenu ces images avec un logiciel de conception assitée par ordinateur que j'avais développé, sans le début des années quatre vingt ) le gif animé suivant montre ce modèle en présentant le point double vers le haut. Le point quadruple est également visible :
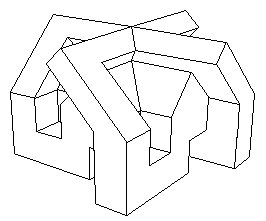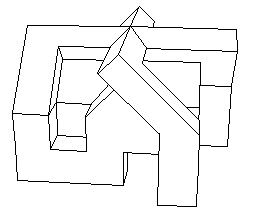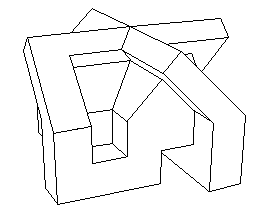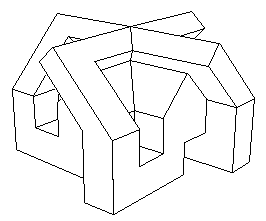
Ma version polyédrique du modèle à quatre oreilles
Comment construire ce modèle à l'aide d'un découpage
Dans l'animation initiale l'objet était "en miroir" par rapport à la vue ci-dessus. Ainsi, "vu d'en haut" il affectait la forme d'une croix gammée, l'ensemble pouvant évoquer une sorte de "maison de la culture pour parti néo-nazi". J'ai préféré inverser l'objet pour ne pas donner à des architectes d'extrême-droite des mauvaises idées. Cliquer ici pour avoir toutes les explications sur la façon de monter vous-même cet objet. Pour finir, quelques vues de cet objet.
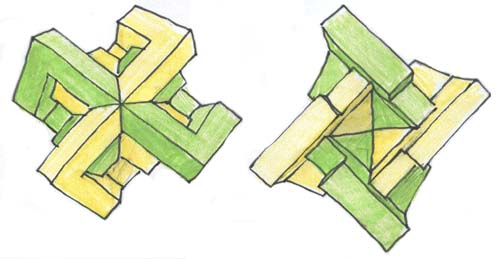
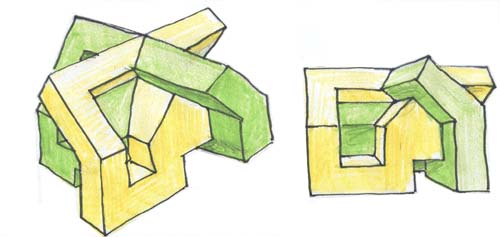
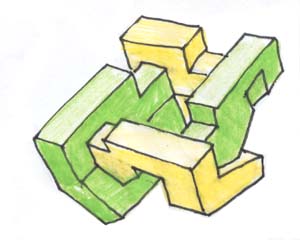
Je finirai cette évocation du retournement de la sphère par une anecdote étonnante quoique parfaitement authentique. A l'époque où ces transformations n'étaient connues que par un nombre infime d'initiés un mécène offrit un prix d'un million de dollars à la personne qui parviendrait à construire des modèles suffisamment explicite. A Berkeley, le mathématicien Charles Pugh s'attela à ce travail et le mena à bien. Avec l'argent il put acquérir une maison. Ces modèles, réalisé avec du grillage à poules et mesurant chacun un bon mètres de diamètre ( Pugh parvenait avec une dextérité étonnante à couper et à rattacher les mailles de ses structures en permettant l'auto-traversement ) ornèrent pendant des années le plafond de la cafétéria du département de mathématiques de Berkeley. Puis, une nuit, ils furent volés et on ne les retrouva jamais. On ne sut jamais qui avait fait le coup. Commercialement c'eût été plus difficile à vendre que la Joconde du Louvre. Peut-être un amateur les détient-il dans une cave secrète en se réjouissant chaque soir d'y descendre en se disant "je suis le seul à pouvoir les contempler".
Il y a une autre anecdote qui se réfère cette fois à la surface de Boy, dont j'ai été le premier à situer les courbes méridiennes, en les identifiant à une famille d'ellipses. Ce travail fut effectué de manière totalement empirique, à partir d'un modèle en métal que j'avais réalisé. Un des fils du mathématicien Jean-Marie Souriau, Jérôme, poursuivait alors des études de physicien. En utilisant le micro ordinateur Apple II de son père il parvint à construire la première représentation paramétrique de cet objet, du type :
X = X ( alpha , mu )
Y = Y ( alpha , mu )
Z = Z ( alpha , mu )
Je suis infoutu d'inclure la police de caractère
Symbol dans Dreamweaver, qui me permettrait d'inclure des lettres Grecques dans
une page htm
&&& Si quelqu'un pouvait m'expliquer comment procéder......
A l'aide de dix lignes de programme BASIC nous pûmes faire apparaître sur l'écran pour la première fois, en 1981 des images fil de fer" de la surface de Boy. Si vous trouvez d'ailleurs des images de synthèse de cet objet dans des sites, elles auront toujours été obtenue à partir de ce travail publié à l'Académie des Sciences ( tome 293 , séance du 5octobre 1981, série 1 pp. 269-272 ). Comme ce travail est signé J.P.Petit et J.Souriau, les (rares) lecteurs pensent que J. Souriau est le mathématicien bien connu. En fait il s'agit de son fils Jérôme, qui ne termina jamais sa licence de physique et préféra exercer le métier d'informaticien. Il est facile de se rendre compte que les images de synthèse, dont beaucoup ont été créées par le polytechnicien Colonna à l'Ecole Polytechnique sont basées sur ces équations que nous avions trouvées, Jérôme et moi. Elles demandraient à être améliorées et, faut de ce travail de finition, la surface présente trois plis assez inesthétiques au voisinage de son pôle. Voici le programme permettant de construire ces représentations "fil-de-fer".
Le programme, extrait du Topologicon :
![]()
La dernière anecdote est plus étonnante.
Il y a une vingtaine d'années je participais à une expédition
sous-marine au sud de Bahamas, avec le plongeur Jacques Mayol. Le but était
de découvrir une "pyramide engloutie" dont l'existence avait
été mentionné par Charles Berlitz dans son célèbre
ouvrage "le Triangle des Bermudes", best seller planétaire.
Pour être précis cette pyramide aurait du se trouve au sud du récif
Cay Sal Bank, à mi-distance entre la Floride et Cuba, une région
infestée de requins de haute mer, passablement dangereux. Mais en matière
de recherche il faut parfois savoir prendre des risques.
Nous ne trouvâmes pas plus de pyramide que de beurre en broche. Nous avions été amenés à pied d'oeuvre par un financier italien très riche, sur un yacht magnifique, de trente mètres de long, équipé de très puissants moteurs. Faute de pyramide, je me mis à parler à ce milliardaire de géométrie en lui précisant qu'en sponsorisant la création de surface mathématiques il trouverait là un moyen de dépenser son argent, encore plus inutilement qu'en invitant à dîner des girls du Lido de Paris. L'homme, dont je tairai le nom, mais dont le véritable prénom est Carlo accepta de financer la réalisation de quelques modèles, qui furent "mis au net" par un plasticien plus adroit que moi dans la manipulation du fil de fer cuivré. A terme ce financier voulait faire réaliser des modèles faits avec du fil d'or, pour les mettre dans son salon.
Un jour, soudain, le contact se trouva rompu. Je finis par tenter de le joindre dans ses bureaux de Milan. Mais j'appris qu'il avait été incarcéré, ayant été identifié comme le numéro deux de l'affaire de la " Loge P2 " en Italie. Il put sortir de prison quelques mois plus tard en achetant ses juges. A mon grand regret l'italien se détourna désormais des mathématiques. Au passage ceci nous permit de comprendre quel avait été le but réel de l'expédition aux Bahamas. En fait son magnifique Yacht avait servi à transporter d'Italie à Nassau, au Bahamas, de l'argent sale, probablement issu du trafic de drogue. Lorsque nous avions fait escale dans ce port le propriétaire du bateau, notre hôte, avait disparu dans une cachette qu'il avait aménagée dans celui-ci, d'où il émergea quand la police du port, ayant effectué son inspection et vérifié l'identité des personnes présentes à bord, était retourné à terre. Il prit alors la direction de sa banque de Nassau, porteur d'un attaché case au contenu visiblement très pesant, qui devait sans doute contenir une véritable fortune en argent liquide. A cette époque, nous nous demandions comment nous allions faire pour ne pas nous faire dévorer par les requins à Cay Sal Bank nous n'avions pas sur le moment accordé de l'importance à ce détail, qui ne m'est revenu en mémoire que par la suite.
Au retour en France je fis cependant l'erreur de raconter au responsable du département de mathématiques du Palais de la Découverte de Paris, situé au Grand Palais, que le modèle que je lui proposai d'exposer, et qui le fut effectivement pendant une vingtaine d'années, avait été réalisé avec de l'argent issu du commerce de la drogue. Par précaution, celui-ci s'abstint d'apposer à côté de l'objet une mention quelconque, pas même le nom de son inventeur, où le mien. Celui-ci trôna ainsi au centre de la "salle pi" pendant deux décennies, de manière totalement énigmatique.
On a parlé jadis d'un malédiction attachée à la découverte du tombeau de Tout Ankh Amon. Je ne sais pas s'il existerait une " Malédiction de la Surface de Boy ". Toujours est-il ( et cela est parfaitement authentique ) que son inventeur se volatilisa mystérieusement et que cet objet, tel le Faucon Maltais du film avec Humphrey Bogart resta attaché à des histoires liées à la Mafia sicilienne. Je me demande si le retrait de celui-ci et son placement dans une cave du bâtiment ne fut pas de la part de la Direction du Musée une simple mesure de prudence.
Les réserves du Palais de la Découverte, non accessibles au public, sont semblables à un tombeau pharaonique souterrain de la Vallée de Rois égyptienne. Peut être un explorateur, des années après que la II° guerre mondiale ait atomisé Paris, découvrira-t-il par hasard cet objet, qui fera peut être de nouvelles victimes, qui sait ?
Retour vers Nouveautés Retour vers Guide Retour vers la page d'Accueil
Nombre de consultations de cette page depuis le 8 décembre 2004 :