Le modèle Central du Retournement du Cube
31 déc 2001
Vous avez tous vu tourner, inlassablement, un objet bizarre sur la partie gauche de la page d'accueil du site. De quoi s'agit-il ?

Un jour, quand j'aurai du temps, j'installerai sur le site une description du retournement de la sphère, tel que je l'avais illustré dans le numéro de janvier 1979 de Pour la science, c'est à dire il y a ... 22 ans de cela. Tout cela demanderait évidemment force détails et introduction. Retourner une sphère, qu'est-ce que cela veut dire ? Une sphère n'a pas la même signification pour l'homme de la rue et le mathématicien-géomètre. Pour l'homme de la rue, celle-ci se définit comme étant, dans un espace à trois dimensions, comme le lieu des points situés à une distance R d'un point fixe O de celui-ci. Un géomètre continuera à appeler "sphère" un objet qui correspondrait à une "sphère déformée", une sorte de "patate". Pour appréhender tous ces concepts avec plus de précision, procurez vous le CD Lanturlu porteur de la bande dessinée "Le Topologicon". Mais le mathématicien va même plus loin. Quand une surface est dite "régulière" on peut en chacun de ses points définir un plan tangent. Cela permet déjà d'envisager une infinité de déformation de la "sphère de départ" en une infinité de patates, quand de plus l'aire de la dite surface peut être quelconque. Ceci étant, dans une "univers physique" la personne qui déforme cette sphère se heurtera à l'impossibilité de la faire se traverser elle-même. Si ces traversements ou même ces contacts sont interdit, on parlera alors de plongements de la sphère S2. Mais un mathématicien se donne tous les droits. Une sphère est, pour lui, un objet "virtuel" où les traversements de nappes deviennent possibles. La suite de dessins ci-après montre une sphère qui s'est "auto-traversée". On appelle alors cette représentation de la sphère une immersion.
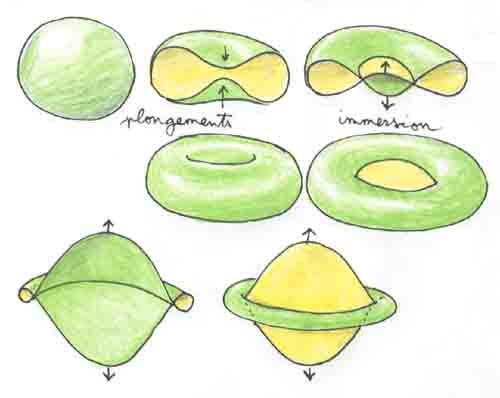
Une immersion possède un ensemble d'auto-intersection ou de self-intersection (ici une simple courbe circulaire). Le plan tangent doit varier continument. Ceci étant, quand on regarde les dessins ci-dessus, on voit que l'opération tourne bien une partie (représentée par la couleur verte) de l'intérieur de la sphère vers l'extérieur. Pour achever un tel retournement il faudrait écraser cette sorte de boudin équatorial. La chose semble a priori problématique. Cet écrasement romprait la continuité du plan tangentl L'opération comprendrait donc une étape qui ne serait pas une immersion.
Un jour un mathématicien américain, Stephen Smale, démontra que "La sphère S2 ne possédait qu'une seule classe d'immersion". Le corollaire de cette phrase sybilline était qu'on devait pouvoir enchaîner une séquence d'immersions de la sphère permettant de passer de la "sphère standard" à sa représentation "antipodale", c'est à dire dont tous les points auraient été remplacés par leur antipode. Bref ... une sphère retournée, recto-verso. Raoul Bott était le patron de Smale. Autant la démonstration de ce dernier, purement formelle, semblait sans faille, autant personne ne voyait comment s'y prendre pour réaliser l'opération. Bott disait sans cesse à Smale "montrez-moi comme vous envisageriez de procéder", ce à quoi Smale, avec son célèbre cheveu sur la langue répondait "je n'en ai pas la moindre idée". Smale eût par la suite la médaille Field, équivalant au prix Nobel,mais pour les maths. Au passage, vous vous demanderez peut-être pourquoi Nobel n'avait jamais voulu créer de prix Nobel des mathématiques. La réponse est simple : sa femme est partie avec un mathématicien.
Les choses restèrent en l'état pendant pas mal d'années jusqu'à ce qu'un mathématicien américain nommé Anthony Phillips ne publie en 1967 dans Scientific American une première version de ce retournement, atrocement compliquée. La seconde fut inventée au début des années soixante-dix par le mathématicien français (aveugle) Bernard Morin. Je fus le premier à dessiner cette suite de transformations qui fera, je l'ai déjà dit, l'objet d'un prochain papier dans le site, assez copieux d'ailleurs. Toujours est-il que ceci nous amène à une conclusion annexe. Les surfaces peuvent faire l'objet de représentations polyédriques. Un cube ou un tétraèdre peuvent être considérés comme des représentations polyédriques de la sphère, dans la mesure où ces objets ont la même topologie. Sur ce point, consulter ma BD le Topologicon. En outre, on comprendra que s'il est possible de retourner une sphère, il est également possible de retourner un cube. La transformation inventée par Bernard Morin (que j'ai illustrée dans l'article de janvier 1979 de Pour la Science) passe par un modèle central. Il existe une symétrie dans cette séquence. C'est ce qu'on appelle "le modèle central à quatre oreilles". Là encore, j'anticipe. Mais de même que la sphère peut se préter à des représentations polyédriques, il en est de même pour les étapes successives de ces transformations. L'objet que vous voyez tourner sur ma page d'accueil est ainsi la version polyédrique du modèle central du retournement de la sphère, un modèle que j'ai inventé il y a une dizaine d'années. L'intérêt de ces modèles polyédrique est qu'on peut les construire avec des surfaces planes. On peut même les agencer selon des découpages. Jetez un oeil au dessin ci-après (je remercie au passage mon ami Christophe Tardy, qui en a produit les éléments correctement cotés).
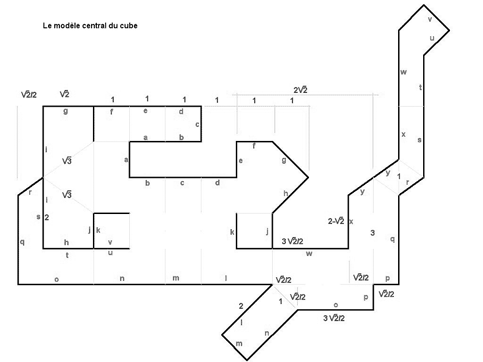
Ceci est un dessin qui sortirait sur votre imprimante en petit format, inexploitable.
Pour imprimer cette figure sur
une feuille A4
Il faut alors en faire quatre photocopies sur du papier
fort A4, deux feuilles d'une couleur, deux feuilles d'une autrte
C'est un découpage dont vous avez ici une vue générale. Mais pour l'imprimer il est préférable que vous passiez à la page découpage. Imprimez-là. Puis, muni de cet exemplaire imprimé sur le papier normal de votre imprimante, allez chez un photocopieur et réalisez quatre copies à l'identique de ce dessin, deux sur deux feuilles de bristol vert et deux sur des jaunes. Vous allez être en mesure, à l'aide de ce découpage, de construire le modèle central du retournement du cube.
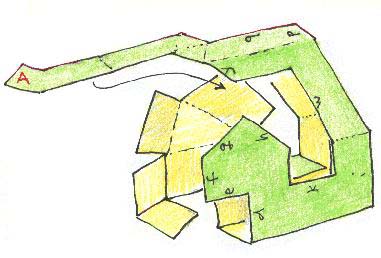
Vous avez, sur ces éléments découpés, des paires de lettres : a , b c , d , e , f etc.... Il vous suffit d'opérer les pliages en amenant les mêmes lettres en coincidence, puis en assemblant ces facettes avec du ruban adhésif transparent. Les dessins qui suivent montrent la façon de monter l'un des quatre éléments. Voici d'abord comment il faut débuter le pliage d'un des quatre éléments :
 |
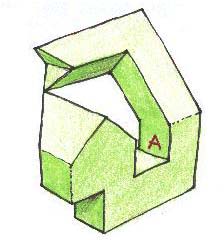 |
Voici deux de ces quatre éléments, vus sous des angles différents.

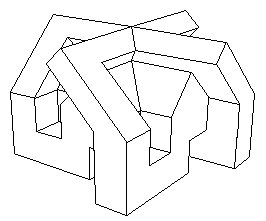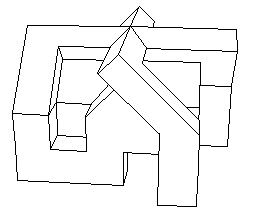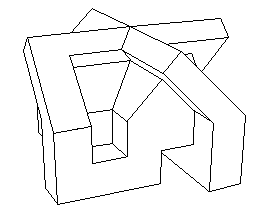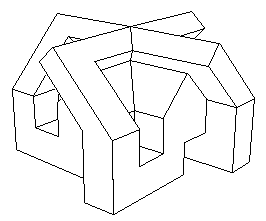
Ceux-ci s'agencent ensuite pour donner un objet ayant une symétrie d'ordre quatre ou alternent des éléments verts et des éléments jaunes. Pour voir ceci en 3d, allez jeter un oeil aux réalisation du sieur Tardy, en "virtual reality". Le modèle central totalement assemblé est aussi produit en "vrml" dans cette section. Voici cet objet, vu sous différents angles :
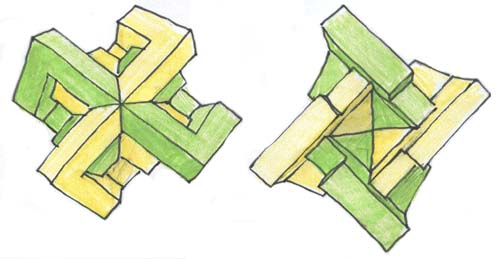
On ne peut pas dire qu'une vue correspond au "dessus" et l'autre au "dessous" puisque ces dénominations seraient totalement arbitraires. Sur la vue de gauche le point "central" correspond au "point double" (où deux nappes se croisent) du modèle central de Morin, tandis que le point central de droite équivaut au "point quadruple" de ce même modèle (où quatre nappes se croisent). J'ai du soigneusement orienter l'objet, pour que la figure de gauche n'évoque pas une croix gammée. Sinon, architecturalement parlant, cette représentation polyédrique du modèle central de Morin aurait pu constituer un très bon projet de maison de la culture Nationale Socialiste.
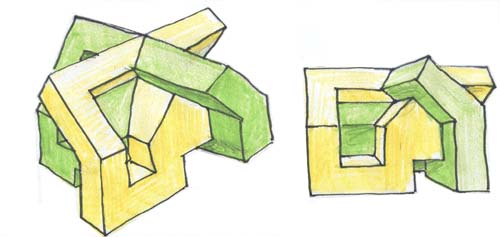
Dernière vue :
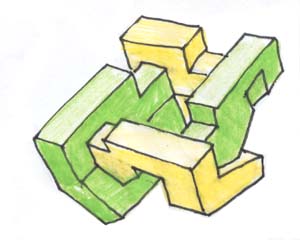
Une dernière remarque : il n'existe pas de bonne représentation polyédrique du retournement de la sphère (alias le retournement du cube). Par "bonne" il faut entendre une suite de modèles suffisamment explicites qui peuvent être montés sous forme de découpages de manière relativement facile, comme le modèle ci-dessus. Une recherche serait à faire en ce sens, qui est à la portée de n'importe qui, éventuellement d'un non-mathématicien, d'un plasticien, par exemple. Il y a plus de vingt ans j'ai été enseignant en sculpture à l'Ecole des Beaux-Arts d'Aix en Provence, du temps où celle-ci était encore dirigée par mon excellent ami Jacques Boullier. C'est dans ces locaux que naquit la première représentation méridienne de la surface de Boy à l'aide d'ellipses, clef de la construction de la première équation implicite par Apéry. je dois dire qu'à l'époque j'ai toujours été surpris par l'imagination géométrique des étudiants en art, qui surpassait très souvent celle... des géomètres.
Compteur initialisé le 31 décembre 2001. Nombre de connexions :
Retour vers le sommaire maths Réalité virtuelle Retour vers Nouveautés