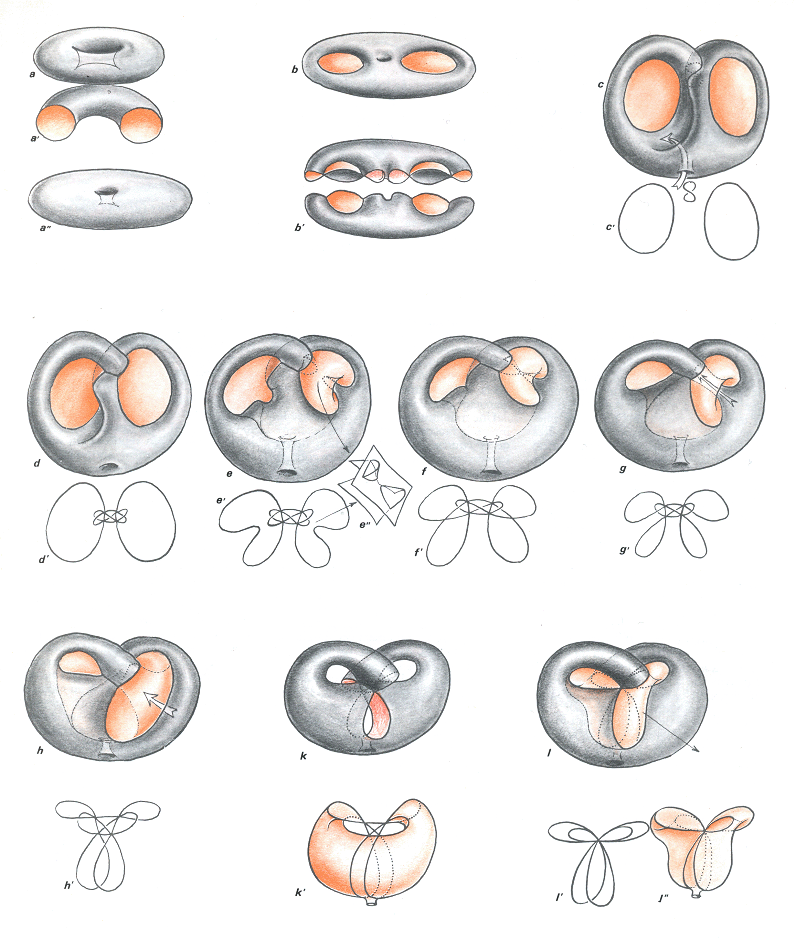
Le Retournement du Tore

9 décembre 2004

page 6

Le retournement non trivial du tore

J.P.Petit :

Comptes Rendus Académie des Sciences.
tome 293 , séance du 5octobre 1981, série 1 pp. 269-272

Je me contenterai de présenter la suite des dessins, sans les commenter.

Retournement non trivial du tore. Première partie de la transformation

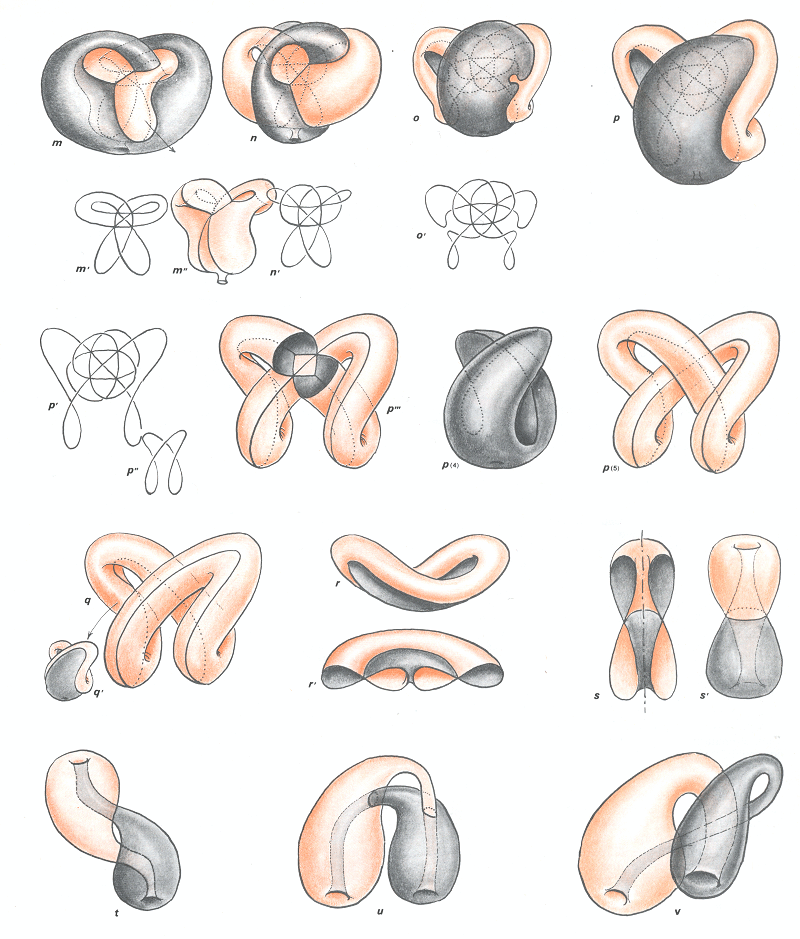
Retournement non trivial du tore. Seconde partie de la transformation

Quand on arrive à la figure v on voit qu'il est alors aisé de faire coincider la structure grise et la structure rose pour transformer cet objet en revêtement à deux feuillets de la bouteille de Klein.

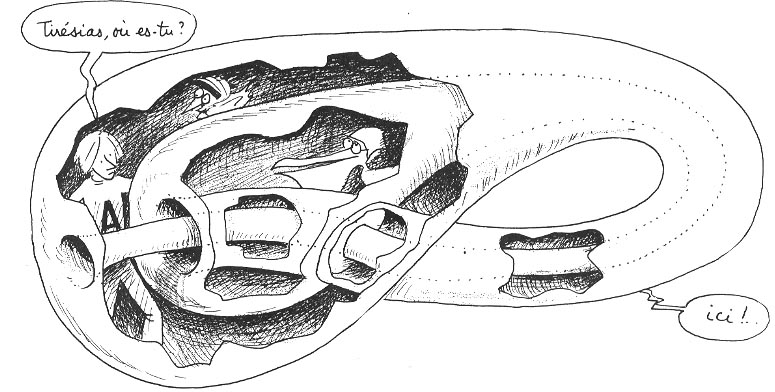
Le retournement s'opère alors par échange des nappes en regard. Ci-après, le même dessin avec un codage chromatique.

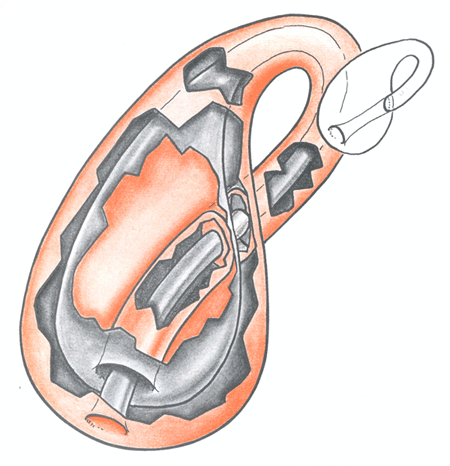
Revêtement à deux feuillets de la bouteille de Klein, avec codage chromatique

( ce dessin ne faisant pas partie de mon rapport annuel au Cnrs. On le trouvera dans le Topologicon )

Les différentes familles de tores.

Ce qu'avait démontré Stephen Smale en 1957 c'était qu'il n'y avait qu'une seule famille d'immersions de la sphère et que toutes celles-ci pouvaient être reliées entre elles par une homotopie. Celles-ci formaient un groupe dont l'élément neutre consistait à laisser l'objet en l'état. On se demanda s'il pourrait en être de même pour le tore. Les mathématiciens Ioan James et Emery Thomas ont montré que les immersions du tore se répartissaient en quatre continents entre lesquels il était impossible de passer à l'aide d'une homotopie régulière.

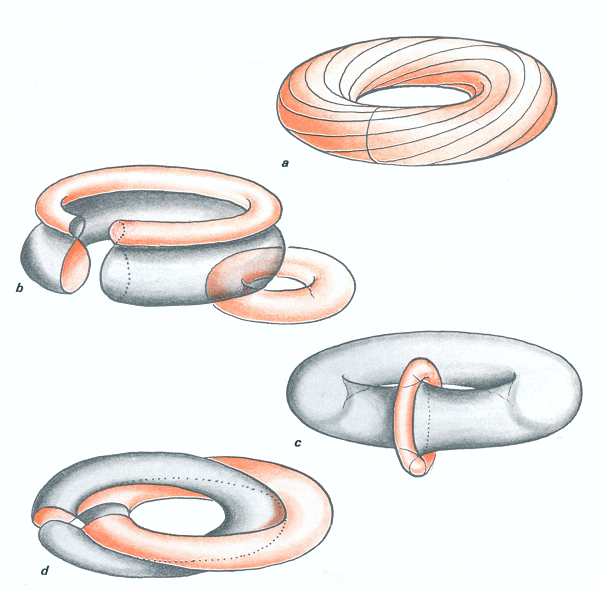
Les quatre familles de tores

Le "tore standard", dessiné au centre de la feuille, appartient à la même famille que l'objet figuré en b. C'est ce que j'ai au passage montré dans la version du retournement du tore que j'ai inventée en 1980. La famille évoquée en a représente un tore qui a subi un vrillage de 360°. Il ressemble au tore standard mais les deux se définissent à partir de leur système de cartographie, à l'aide de deux familles de courbes. Dans le tore standard on utilise deux ensembles de cercles assimilés à des méridiens et à des parallèles. Sur le tore a on devrait compléter la famille de cercles collée dessus par une seconde famille, se vrillant en sens inverse. Ce qu'on peut montrer alors c'est qu'il est impossible, à l'aide d'un homotopie régulière d'amener le maillage de ce tore a en coincidence avec le maillage du tore standard ( cercles méridiens plus cercles parallèles ). C'est en ce sens que ce sont des objets différents. Tous ces objets peuvent évidemment se configurer selon un revêtement à deux feuillets de la bouteille de Klein.

La puissance des outils du géomètre est de pouvoir prédire ce qui est possible et ce qui ne l'est pas. Transformer le tore standard en tore de la figure b : oui. Passer de c à d : non.

Ca évite de perdre son temps bêtement et ça incite surtout à rechercher des choses qui ne sont en rien évidentes, comme de retourner une sphère. Il en est de même dans toutes les sciences. Il arrive que les gens passent à côté de démarches fécondes, pendant des années ou même des siècles, simplement parce qu'ils les croyaient impossibles à effectuer. J'ai consacré quelques années de ma vie à construire une théorie de la suppression des ondes de choc autour d'un objet se déplaçant à vitesse supersoniques dans un gaz, à l'aide d'un champ de forces de Laplace, de la " MHD ". Un étudiant a même fait sa thèse sur ce sujet sous ma direction et nous avons publié ces travaux dans différentes revues à comité de lectures et colloques scientifiques. C'est un thème qui commencent seulement à faire surface, trente ans après. On subodore que les Américains disposeraient d'avions hypersoniques capables d'évoluer à Mach 10 sans créer d'onde de choc (et en particulier sans subir les formidables contraintes thermiques liées à la recompression de l'air derrière ces "bangs". C'est le fameux mythe de l'Aurora, appareil croisant à l'altitude où se produisent les aurores boréales, entre 80 et 150 km d'altitude. Aurora est aussi la préfiguration des futirs lanceuirs spatiaux qui, s'appuyant sur l'air, seront beaucoup plus économiques que les fussées du Cnes. Il a été impossible, en France, d'initier de telles recherches (j'ai eu ces idées en 1975), parce que les gens, en particulier au Cnrs, les trouvaient totalement déraisonnables. Le résultat représente trente années de retard vis à vis des Etats Unis, à mon avis totalement irrattrapables.

La blague à tabac

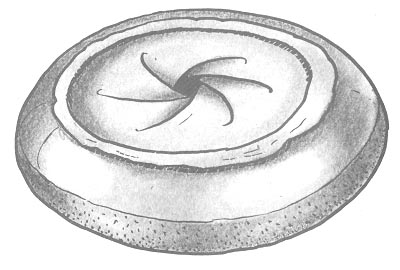
Pour être complet il faut citer les versions du retournement de la sphère ayant pour objet central une blague à tabac. C'était un objet qui était courant quand j'étais jeune, mais qu'on ne doit plus guère rencontrer aujourd'hui. Le premier qui ait dessiné ces séquences est Georges Francis. Depuis quelques années je travaille sur une version polyédrique de ces versions, qui a déjà donné un modèle central assez joli. Mais, pour vous le montrer, il faudra que j'arrive à remettre la main dessus. Assez vite, j'espère, car c'est un des objets les plus fascinants que j'aie jamais créé.

Page précédente                      Page suivante

Retour vers Nouveautés             Retour vers Guide            Retour vers la page d'Accueil

Nombre de consultations de cette page depuis le 8 décembre 2004 :