Le Retournement de la Sphère
7 décembre 2004
page 3
Les catastrophes élémentaires.
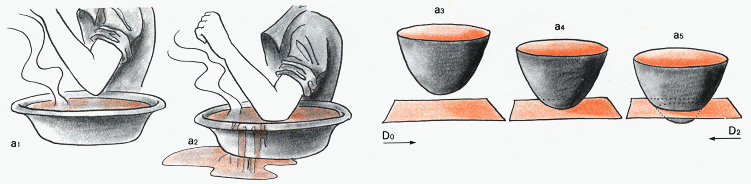
Nous avons déjà dit plus haut que les immersions que nous considérions étaient telles que les plans tangents le long de leurs ensembles d'auto-intersection, quand celles-ci en étaient dotées, restaient distincts. Il est alors possible de passer d'une immersion à une autre à l'aide de quatre catastrophes élémentaires. Morin leur avait donné des noms, qui figurent sur les dessins ci-après. La première conduit à la création d'une courbe fermée (et sa décréation, opération inverse). C'est ce qui se passe lorsqu'on plonge son coude dans l'eau d'une cuvette pour apprécier sa température ( à gauche ). Figure a4 : les surfaces sont en contact en un point. En a5 la courbe d'auto-intersection a été créée. Dans la suite du texte nous appelerons cette opération "la catastrophe du coude".

La " catastrophe du coude" : création - décréation d'une courbe fermée
La seconde catastrophe est celle de la "tranche de mandarine" :
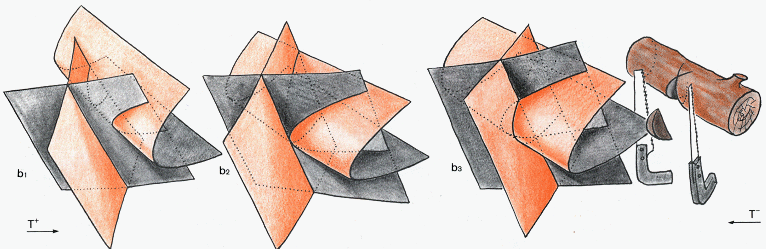
La catastrophe consistant en la création-décréation d'une "tranche de mandarine".
Si on regarde bien ces images, de la gauche vers la droite on verra qu'un cylindre parabolique s'approche d'un dièdre. L'ensemble d'auto-intersection est constitué par deux courbes d'allure parabolique, disjointes, plus évidemment l'arète du dièdre. Dans la figure du centre l'arète du dièdre est en contact avec une des génératrices du cylindre. Cette arète est tangente au cylindre en ce point. L'ensemble d'auto-intersection est constitué par deux courbes d'allure parabolique, tangentes en un point, et à l'arète du dièdre. Figure de droite : le cylindre parabolique a poursuivi son mouvement. La courbe d'auto-intrsection s'est modifiée. Elle est constituée par l'arète du dièdre, plus les courbes paraboliques qui se recoupent en deux points, situés sur l'arète du dièdre. On peut considérer à l'inverse que le cylindre parabolique est immobile et que ce sont les deux "plans de coupe" qui se déplacent. La figure de droite évoquerait alors deux coups de hache, ou deux découpes effectuées à la scie. Le copeau est également figuré. Morin le comparait à une "tranche de mandarine", image très parlante.
La troisième catastrophe est celle "du pantalon".
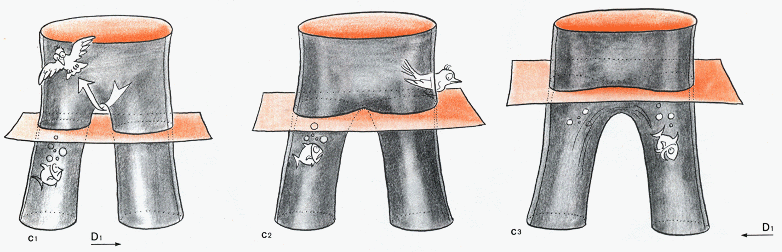
La catastrophe "du pantalon"
Les images sont suffisamment parlantes. On descend de gauche à droite un pantalon dans l'eau. A gauche l'oiseau passe sous l'entre-jambe mais le poisson reste confiné dans une des jambes. A droite le poisson passe, mais le passage qu'empruntait l'oiseau a disparu. Au centre la situation intermédiaire. Ce qui compte c'est la modification locale de la courbe d'intersection, qui correspond à ce qu'on appelle une "chirurgie", un changement de raccordement d'arcs de courbe. Essayez de bien intérgrer cette transformation qui s'avérera la plus difficile à mettre en oeuvre et à bien voir dans l'homotopie du retournement de la sphère. Retenez bien que cette catastrophe ferme un passage en même temps qu'elle en ouvre un autre dans la direction perpendiculaire.
La quatrième et dernière catastrophe est celle de " l'inversion d'un tétraèdre " :
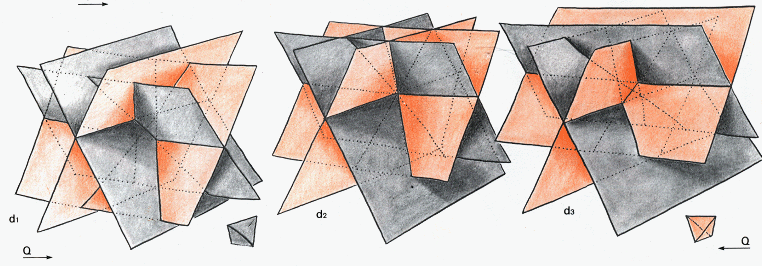
La catastrophe inversant un tétraèdre
La courbe d'auto-intersection en constituée par quatre "droites" qui sont les prolongements des quatre côtés d'un tétraèdre. Dans la figure de gauche on a isolé ce tétraèdre qui montre ses faces grises vers l'extérieur. A droite, c'est l'inverse : les faces sont roses. Au centre, situation intermédiaire : le tétraèdre est réduit à un point Q (quadruple, puisqu'il est à l'intersection que quatre nappes).
A l'aide de ces quatre catastrophe nous allons envisager de retourner une sphère selon une suite continue d'immersions transverses. Cette variante est due au mathématicien (aveugle) Bernard Morin. Notre rencontre vaut la peine d'être contée. Un jour un technicien de la faculté des lettres me demanda d'apporter mes talents de dessinateur à un conférencier qui devait parler de géométrie. Je vins à ce rendez-vous sans aucune méfiance. j'avais toujours été assez habile pour voir les objets dans l'espace et lorsque notre professeur de mathématiques supérieures nous donnait à traiter un problème de géométrie descriptive je traçais l'intersection et je fournissais une vue en perspective en même temps qu'il produisait son énoncé. Mais là, les choses allaient se passer différemment.
Je n'eus aucune difficulté à dessiner les figures ci-dessus. Mais quand il fallut les intégrer dans un schéma impliquant le retournement de la sphère je finis par perdre complètement les pédales, confronté à tout un ensemble de nappes situées les unes derrière les autres. Pîqué ai vif je revins voir ce personnage étrange qui, bien que prové de la vue semblait plus à l'aise que moi dans ce déploiement de formes. Je suivis alors ses cours pendant plusieurs mois. Le dialogue était assez compliqué. De son côté il n'avait que le recours à la parole. Du mien je pouvais soit lui décrire mes dessins, soit mettre entre ses mains des maquettes réalisées en rentrant chez moi, ou par la suite sur place. Il aurait fallu enregistrer ces dialogues, absolument surréalistes, du genre :
- Essaye d'imaginer deux courbes qui viendraient se rejoindre en constituant une sorte de fouet à battre les oeufs.
En dépit de la personnalité difficile du personnage ces rencontres restèrent pour moi inoubliables. Je finis seulement par prendre l'habitude d'avaler deux aspirines avant nos séances de travail, à titre préventif. Son caractère peut être résumé dans le sobriquet dont son épouse l'avait qualifié : "Foudre bénie", lequel est un personnage de la bande dessinée d'Hergé "Tintin au Tibet". Ses rancunes de Morin avaient un caractère aussi légendaire qu'irréversible. Il lui arrivait d'évoquer certains de ses ennemis, qui avaient passé l'arme à gauche, en lançant à leur propos :
- Je leur jette parfois une petite malédiction dans l'au-delà, en me disant que si ça ne leur fait pas de mal, au moins ça ne peut pas leur faire de bien.
Retour vers Nouveautés Retour vers Guide Retour vers la page d'Accueil
Nombre de consultations de cette page depuis le 8 décembre 2004 :