20) More about imbedding and geodesics.
All surfaces
cannot be imbedded in R3. For example, consider the metric
(134)
where Rs > 0 and r > 0
is defined on R modulo 2 
Expressed with those [ r , ] peculiar coordinates,
this line element is regular almoste everywhere (except at the point r = 0).
Elsewhere no problem arises. Its isometric group is O2. The orbits of the group
are circles r = constant. We could imagine that this surface could be imbedded
in R3, where it would appear axisymmetric, around some z-axis.
( = constant ) geodesics exist. We could think that they are "meridian lines"
of the surface and that the equation z ( ) of such
meridian can be built as we did at the begining of the paper. Along ( = constant ) geodesics :
(135)
If this
surface can be imbedded in R3, along those geodesics :
(136)
which gives :
(137)
Conclusion : this surface cannot be imbedded in R3.
This metric (135) evokes some repulsive action.
All surfaces, as defined
by their metric, cannot be. Anyway, these surfaces "exist", even if
we cannot grasp them in our hands.
Consider the following
3d hypersurface, as defined by :
(138)
with Rs > 0 and r > 0
is defined on R modulo 2
We cannot imbed such hypersurface.
But it exists and owns "plane geodesics" ( 
= /2).
We may compute the geodesic
system of these 2d and 3d hypersuface. We can figure them in a plane (r,).
They are real.
(139)
Their design is identical to the ones of the precedent 2 surface, as defined by its line-element (134). These two geometric objects are simply connected.
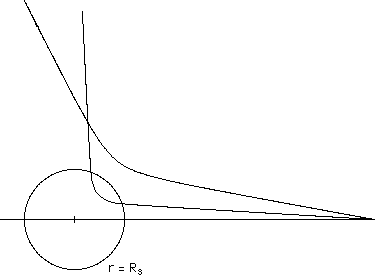
Fig.25
: Geodesics corresponding
to line elements (134)
and (138)
(Notice that it is similar to a repulsion action).
There is something
puzzling. Given a line-element, we can compute the geodesic system. For example
the one of the classical representation of Schwarzschild geometry corresponds
to :
(140)
We may calculate the curves
r () corresponding to this differential equation.
They are real, including
for r < Rs values !
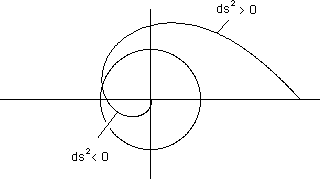
Fig.26 :
Complete geodesic line, correspond
to Schwarzschild
line element.
We understand why physicists were puzzled, after looking at this strange result. But there is a mathematical fact : a line element may produce a real geodesic system, some portions corresponding to imaginary length element ds.
What about physics ? We identify ds as a proper time increment. Above we have decided to consider that imaginary ds does not correspond to physical path, which obliged us to reconsider the "local topology" of the hypersurface, changing the "local spheroidal topology" into a "local hypertoroidal topology".
In previous works people kept this "local spheroidal topology" hypothesis, so that the physical interpretation of the "inside" of the Schwarzschild sphere became problematic. In reference [1], in section 6.8 we read :
(Inside the Schwarzschild
sphere) it would thus appear natural to reinterpret r as a time marker
and t as radial marker (...)
... that would imply that ds2 < 0 along this world-line.
21) The Kruskal analytical extension.
In classical [x° , r ,
, ] coordinate system the radial velocity of
light is :
(141)
so that it tends to zero when r tends to Rs. The Kruskal's argument is the following ( reference [1], section 6.8 ).
This
is an undesirable feature of the Schwarzchild coordinates that we can eliminate
as follows; we seek a transformation for r and t to new variables
u and v in which the line element has the form :
(6.187)
... we arrive to a transformation
appropriate to the interior of the Schwarzschild radius :
(6.204)
While, out of that sphere
:
(6.201)
The basic requirement is that f to be regular on the Schwarzschild sphere r = Rs. Still from [1] :
Thus u serves as global radial marker, and v serves as global time marker.
By the way, from (6.187) , null geodesics (ds = 0) gives a "constant light
velocity" :
(142)
From (6.201) we see that when r tends to infinite f tends to zero, so that Adler, Schiffer and Bazin say [1] :
They do not, however, correspond to spherical coordinates for flat space at asymptotic distance, as the Schwarzschild coordinates do.
The Kruskal metric is also a non singular solution of the Einstein equation in these regions and is equivalent to the Schwarzschild solution, but has no singularity at the boundary (the Schwarzschild sphere). This is an analytical extension of the manifold.
Kruskal concentrates of the problem at this boundary, which becomes non singular, the singularity being concentrated at the "geometric center" where f tends to infinite. Still using reference [1] we reproduce the passage devoted to inwards photon's radial paths :
In terms of u , v the trajectory is simple; in terms of r and t , however, we see that it begins at some finite r > Rs and finite x° , travels inwards towards r = Rs as x° tends to infinite, and crosses the line x° = infinite to the interior of the Schwarzschild sphere. After that r continues to decrease along the trajectory, but x° decreases. ... The present treatment also clarifies that x° is not a reasonable time marker inside the Schwarzschild sphere.
We see that "nothing is perfect". With his peculiar choice of coordinates, Kruskal manages the crossing of the Schwarschild sphere, confining the singular feature of the geometrical solution into a "central singularity". But the metric is no longer Lorentzian at infinite.
This shows how the coordinate choice modifies the interpretation of the solution. Ours introduces a change in the "local topology" (hypertoroidal bridge ), but all singularity is eliminated.
22) Back to imbedding.
The Wiener-Graustein theorem says that any n-dimensional surface, with n >
2, can be imbeded in a spaces whose minimum dimension is
(143)
For 4d hypersurfaces it corresponds to a 10 dimensions space. We know that Schwarzschild
geometry geodesics lie in planes. = p/2 corresponds
to one of them. Then we can concentrate on a subset of (
= p/2) geodesics. These geodesics depend on two parameters l and h .
We know that ( l =1 ) geodesics correspond to particles
whose velocity is zero at infinite.. In addition, choose the subset of ( = constant ) geodesics. Then :
(144)
Introduce an additional coordinate z and write :
(145)
ds 2 = dr 2 + dz 2
(146)
A differential
equation whose solution is :
(147)
We can figure these geodesics in a 3d [ z , r ,]
space. They are meridian lines of an axisymmetric surface.
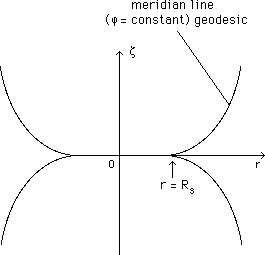
Fig.
27 : The meridian of the surface in which an isometric imbedding
of the ( = constant) Schwarzschild geodesics
is operated.
In 3d space, this surface looks like the figure 28 (an half cut).
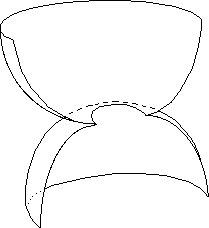
Fig.28 : The imbeding surface.
If we draw the "radial" geodesics on it, we get the figure 29.
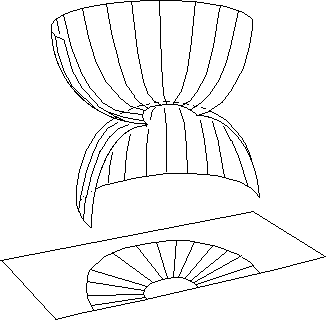
Fig.29
: Representation of "radial" geodesics. Bottom : their projection
on a [ r ,] plane.
It is a very partial imbeding, for it is limited to the set of "radial" geodesics. The figure 29 evokes a pleat and suggests enantiomorphy. In effect, consider a set of three points following radial geodesics. We get
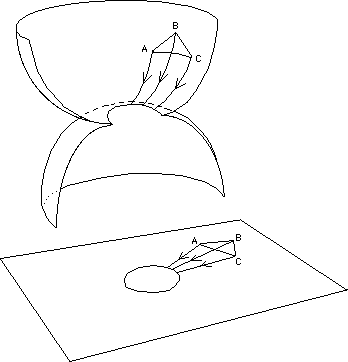
Fig.30-a : Three mass-points, falling towards the throat along "radial" paths.
and :
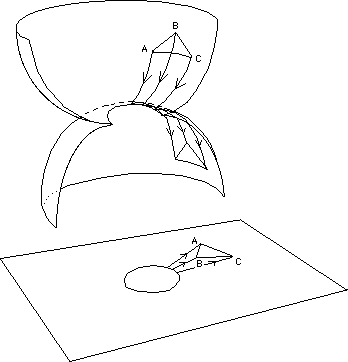
Fig.30-b : The same, after crossing the throat.
The triangle has been inversed.
On the plane projection [ r ,] the orientation
of the triangle is reversed.
Imagine now four test particles following radial trajectories, falling toward
the Schwarzschild sphere, forming a tetrahedron. See figure 31.
Fig.31 :
Four particles falling onto the Schwarzshild sphere along "radial"
geodesics in an euclidean 3d representation space.
Fig.32 :
After "bouncing" on the Schwarzschild sphere the particles travel
in the twin space. The tetraedron is reversed (enantiomorphy)
Let us return to the precedent representation. The normal vector is reversed too :
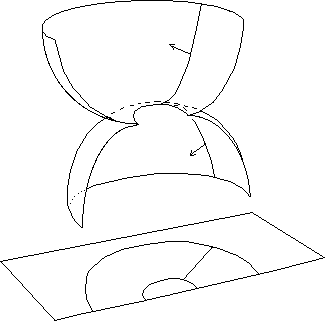
Fig.33
: A peculiar = constant geodesic in its
representation
In the set of (l = 1) geodesics, in a
( r ,, z ) space.