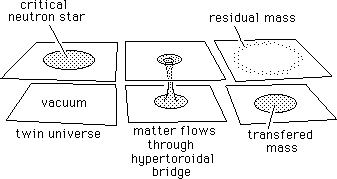
17) Suggestions for hyperspatial transfer models.
Soft scenario :
Assume a neutron star, close to criticity, is located at the vicinity of a companion star. This last sends it matter (stellar wind). When the critical conditions are reached, a small hypertoroidal bridge would form, at the center of the star, which would rapidly evacuate the matter in excess, towards the twin space. This transfered matter behaves like if it mass had been inversed (for it moves in a reversed time marker fold F*, see section 14). The neutron star repels it and it is rapidly sprayed in space, in the twin fold. This process would ensure the stability of the neutron star, for the bridge would get closed when the density and pressure at its center gets reduced enough. This could go with gravitational waves and gamma rays emissions (gamma flashes).
Hard scenario :
Couples of neutron stars exist. It has been shown that their movement of rotation
was continuously slowed down, due to energy loss by gravitational waves emission,
so that they should merge. The abrupt merging of two neutron star would turn
into a catastrophy (including the mathematical meaning of the term). Building
a complete non-steady solution of the system (115) plus (116) would bring a
description of such process. The following is conjectural.
Remark that the full
transfer of matter would lead to a configuration corresponding to :
(126)
S = - c T*
(127)
S* = c T*
But, the process being a priori reversible, the transfered neutron star would be critical. A possibility is an almost complete transfer of matter in the twin space. After the process ends, the hypertoroidal bridge would close, and a new equilibrium would be reached, corresponding to :
(128)
S = - c (T - T*)
(129)
S* = c ( T* - T )
The sizes of the bold letters is supposed to show the relative imprtances of the tensors terms. The small T is supposed to represent the remnant matter, staying in our fold.
How could it look like ?
This remnant matter would be kept at distance by the transfered neutron (self attractive, but repelling the remnant matter, due to the inversion of its mass) , now located in the twin space. As explained is references [13], [14], [15] and [21] :
- Matter attracts matter, through Newton's law (in Newtonian approximation).
- Twin matter (transfered matter) attracts twin matter, through Newton's law.
- Matter and twin matter repel each other, through an "anti-Newton's law".
In our fold, the remnant matter would cool by radiative process. If no energy source exists in its vicinity, its temperature would tend to the cosmic background'one (3°K). It would form some sort of hollow shell of cold gas, surrounding an (invisible) repellent object. See figure 17

Fig.17 : Schema of hyperspatial transfer of the majority of the matter of a neutron star.
If this idea is good, such cold objects would be observable in our galaxy. Perhaps some proplyds (recently discovered), if they are made of cold gas, could correspond to such remnant shells. Of course, if they are located at the vicinity of hot stars, their temperature could not be so low. Some people think proplyds are young stars, or young planetary system, experiencing a formation process. This is just a suggestion.
18) Criticity in a neutron star.
Spherically
symmetrical neutron stars (a somewhat non realistic model) are classically described
by an internal Schwarschild geometry, corresponding to the well-known metric
:
130)
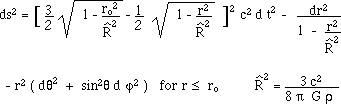
The stability
condition is :
(131)
![]()
We have two characteristic lengths. Left : the Schwarzchild radius. Right : the characteristic radius associated to the internal solution. rn is supposed to be the radius of a (constant density) neutron star. When it tends to criticity, this corresponds to figure 18.
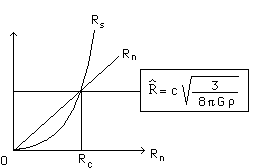
Fig.18 : A neutron star tending towards criticity.
The chapter 14 of reference [1] "The role of relativity in stellar structure
and gravitational collapse" presents in section 14.1 the TOV equation (Tolman-Oppeinheimer-Volkov
model). It is shown that if :
(132)
![]()
the pressure becomes infinite at the center of the (spherically symmetric) neutron star). This critical radius is :
![]()
which is slightly inferior (and corresponds to a smaller critical mass : two solar masses, instead 2.5 ).
It shows that this rise of the central pressure is the first symptom of criticity.
...The figure 19 shows the value evolution of the pressure, inside a neutron star, for different values of the external radius, up to criticty, through TOV model. When the critical neutron's mass becomes critical (for a value close to 2 solar masses), pressure raises up to infinite.
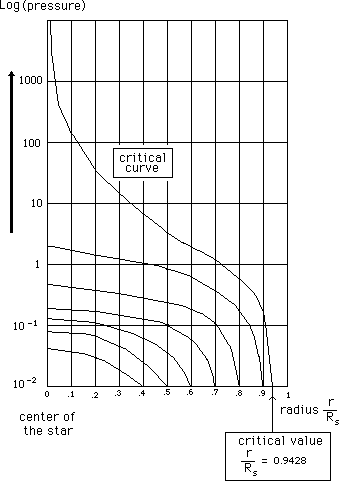
Fig. 19 : Pressure inside a neutron star (TOV model) for different values of external radius.
Following curves are still based on (steady-state) TOV equation, so that it cannot be considered as a correct model. Anyway, it seems to indicate how fast the (p = infinite) sphere could grow inside the neutron star, when the radius increases slightly.
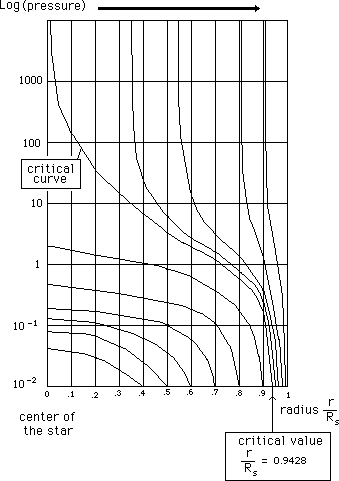
Fig.20 :
Internal pressure computed after steady-state TOV equation.
Although basically
uncorrect this seem to show how fast the singularity (p = infinite)
could grow with slight mass increase.
19) A didactic model of hypertoroidal transfer.
In reference [16] we presented a coupled metrics solution ( g , g*),
describing the geometries of the two folds when a constant density sphere is
present in one fold (ours), with vacuum outside, and when the adjacent portion
of twin space is empty. Il was shown that the local scalar curvatures were conjugated
through :
(133)
R* = - R
A (crude) model of a mass surrounded by void is a blunt cone (assuming that particles follow the geodesics of this surface. See the website). Its blunt part is a portion of a sphere, whose curvature density is constant. The rest is a portion of a cone, an euclidean surface, whose local curvature density is zero.
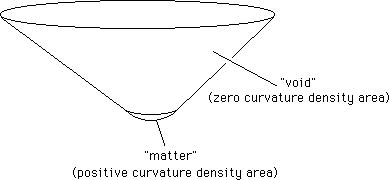
Fig.21a : Classical blunt cone (blunt "posicone").
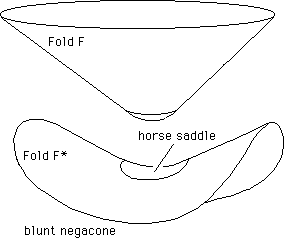
Fig.21b : Blunt posicone with conjugated "twin geometry" : a "blunt negacone (R* = - R)
The conjugated space was then figured as a blunt "negacone", built around a horse saddle, whose constant curvature density is negative, surrounded by a portion of "negacone", an euclidean surface.
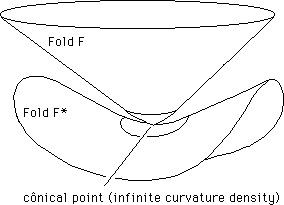
Fig. 22: The two folds get connected through a conical point (infinite curvature density)
Pressure is an energy density per unity of volume. If we figure this pressure by local curvature density, when the critical conditions are reached (infinite pressure at the center of the star), a conical point (which is an infinite density curvature point) appears, and the two folds get connected.
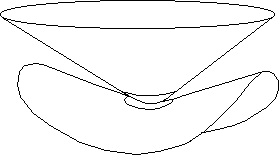
Fig.23 : Apparition of a throat circle.
Then the small passage grows is size, which goes with a modification of the geometrical design.
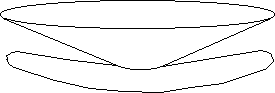
Fig.24-a : which gets enlarged.
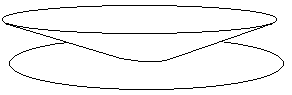
Fig.24-b : The second fold becomes flat.
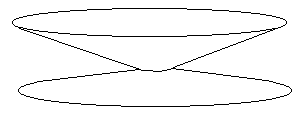
Fig.24-c : The second fold becomes a "posicone".
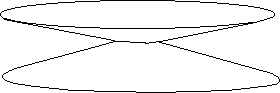
Fig.24-d
: Symmetrical configuration : two truncated posicones linked along a circle
Image of Schwarzschild geometry : The symmetrical "diabolo"
In a symmetrical process, corresponding to the full transfer of matter (positive curvature) towards the twin space the half time would correspond to two truncated cones, connected along a circle. This would correspond to the "Schwarschild's solution".
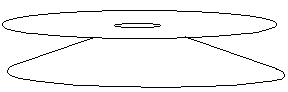
Fig.24-e : The first fold becomes flat.

Fig. 24-f : The first fold F becomes a "negacone".
We can complete the series, and illustrate a process of "curvature exchange" between two surface.
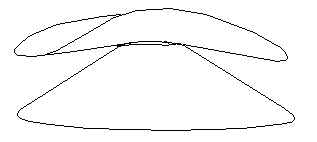
Fig.24-g : The curvature transfer continues.

Fig.24-h : The curvature transfer continues.
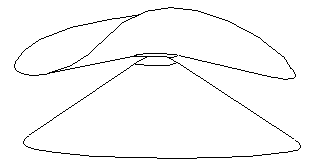
Fig.24-i : The curvature transfer continues.
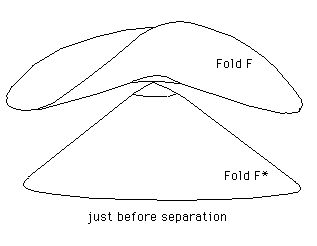
Fig.24-j : Punctual contact, just before separation.
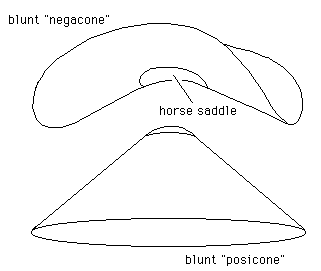
Fig.24-k : End of the curvature transfer.