

...Souriau habite un appartement dans le vieil Aix. La porte donnant sur la rue est splendide. Dans l'entrée se trouve garé un véhicule assez singulier : un chaise à porteur, d'époque, qui appartient à la propriétaire des lieux, une demoiselle, archéologue, je crois. La chaise est contre le mur. Il n'y a plus qu'à trouver deux porteurs, à enfiler les deux longs montants de bois dans les anneaux et à y prendre place pour aller faire un tour. Les ouvertures sont vitrées : les vitres des côtés peuvent se rabaisser, non à l'aide d'une manivelle, mais en manoeuvrant des sangles de cuir, comme c'était le cas dans le compartiments des chemins de fer de mon enfance.
...Comme tout cela fait rêver. Je réalise que je n'ai jamais fait de chaise à porteur. Je suis persuadé, en ces temps de chômage, que des gens pourraient gagner leur vie en montant la première ligne régulière de chaise à porteur dans le vieil Aix. Il suffirait de contruire un véhicule imitant les chaises d'antan. Ca ne doit pas être bien difficile. Puis, se procurer deux habits brodés, deux perruques et en avant. Trajet : le Cours Mirabeau. Cela suffirait largement. Après, il suffirait de rêver, d'avoir un peu d'imagination.
...Jean-Marie
vit seul avec son chat, Pioum, dans son vaste appartement, plein de dorures,
de lambris. Pioum est adorable. Pourtant je n'ai guère d'attirance pour
les chats. Mais celui là est extrêmement accueillant et affectueux.
Nous travaillons en général dans la cuisine, un étage plus
haut. Une petite pièce, sous les combles, dont l'exiguité contraste
avec la taille imposante des pièces du bas. A chaque fois Jean-Marie
essaye pas de me faire boire son breuvage préféré : le
Fernet-Branca, à base d'artichaut, que je trouve positivement exécrable,
mais auquel il attribue toutes les vertus.
...Quand
il fait un tour en ville, il emmène son GPS, qui ne le quitte jamais.
Il est effectivement assez fascinant de se voir guidé par des satellites
situés à quarante mille kilomètre de la rue où on
chemine. Pour avoir une meilleure réception, Souriau a tendance à
marcher dans l'axe de la rue, l'oeil rivé à l'écran à
cristaux liquides. Efficace, semble-t-il, mais quand même relativement
dangereux.
...Je trouve qu'on s'amuse bien, tous les deux. Un soir de décembre, je passai lui rendre visite, et cela donna la conversation suivante.
- Je vais te parler groupes. Tu te rappelles les axiomes ?
- Oui, il y a en a six. Ce sont :
1 - Il existe des éléments a , b , c ... appartenant à un ensemble E
2 - Il existe une opération interne, notée o ("rond"), permettant de combiner deux éléments d'un ensemble.
a appartient à l'ensemble E
b appartient à l'ensemble E
a o b appartient à l'ensemble E
3 - Cette opération est associative :
a o b o c = ( a o b ) o c = a o ( b o c )
4 - Il existe un élément neutre e tel que :
a o e = e o a = a
5 - Tout élément a de l'ensemble possède un réciproque, noté a-1 , tel que :
a-1 o a = a o = e
Ca fait cinq?
- Enfin, cinq, ou quatre, ou un. Il n'y a pas de règle absolue en matière de numérotation d'axiomes. On pourrait tout aussi bien regrouper des axiomes 1 et 2 en un seul :
- Il existe des éléments a , b , c , etc.., appartenant à un ensemble E, doté d'une loi de composition interne satisfaisant :
a appartient à l'ensemble E
b appartient à l'ensemble E
a o b appartient à l'ensemble E
c'est équivalent.
- Bon, cinq, quatre, peut importe. Où veux-tu en venir ?
- Je vais faire disparaître ce que tu avais appelé les axiomes 4 et 5, définissant l'élément neutre et le réciproque, en les remplaçant par l'axiome du sandwich. Au total, les axiomes sont :
1 - Il existe des éléments a , b , c ... appartenant à un ensemble E
2 - Il existe une opération interne, notée o ("rond"), permettant de combiner deux éléments d'un ensemble.
a appartient à l'ensemble E
b appartient à l'ensemble E
a o b appartient à l'ensemble E
3 - Cette opération est associative :
a o b o c = ( a o b ) o c = a o ( b o c )
4 - Soient trois éléments a , b , c , appartenant à l'ensemble E.
Soit l'équation :
a o y o b = c
Elle possède une solution unique.
C'est ce que j'appelle l'axiome du sandwich où le "jambon" y est pris en sandwich entre les éléments a et b, c étant l'entité sandwich. L'axiome signifie :
On peut toujours sortir le jambon d'un sandwich.
et je dis que ces axiomes définissent les groupes, ils sont équivalents aux précédents.
- Cette solution unique y est élément de l'ensemble E, puisque l'opération est interne et associative.
- Bien sûr, cela va sans dire.
- Mais ça va encore mieux en le disant. Je ne sais pas comment tu vas t'y prendre pour retrouver les deux axiomes se référant à l'élément neutre et à l'existence du réciproque, mais je comprends au moins ce qui t'a amené à voir cette idée.
- Je me suis dit "à quoi ça sert ?"
- Exactement. A quoi sert de disposer d'un élément neutre ? Tel quel, cela signifie "si j'ai un ensemble E, et un élément neutre, je peux composer tous les éléments de cet ensemble avec celui-ci et obtenir la même chose". Ca me fait une belle jambe. De même à quoi sert l'inverse en tant que tel ? Quand on fait des calculs sur les groupes, sur un machin quelconque, on se débrouille toujours, à coup de multiplications à droite ou à gauche par des éléments ou leur inverse pour faire apparaître de a o a-1 ou des a-1 o a, qu'on remplace par e, puis des b o e ou des e o b qu'on remplace par b. Ton axiome du sandwich est "fonctionnel".
- Si tu veux. Passons aux théorèmes qui découlent de l'axiome du sandwich. Les premier est :
I - Il existe un élément neutre qui, composé avec lui-même, donne lui-même :
e = e o e
II - Cet élément neutre est unique.
Démonstration :
Partons de l'axiome du sandwich. L'équation
a o y o b = c
possède une solution y unique.
C'est aussi vrai si b = c = a donc
a o y o a = a
possède une solution unique. Multiplions à droite par y :
a o y o a o y = a o y
Appelons a o y = e
...C'est un élément de l'ensemble, puis a et y appartiennent à l'ensemble et que l'opération est interne. Donc il existe un élément de l'ensemble tels que :
e o e = e
...Le théorème I est démontré. Passons à l'unicité, au théorème II. S'il n'y avait pas unicité, il existerait un autre élément de l'ensemble, appelons-le f, qui obéirait à :
f o f = f
On a :
e o e = e
Multiplions à droite par f :
e o e o f = e o f
Re Multiplions à droite par e :
e o e o f o e = e o f o e
Utilisons l'associativité :
e o ( e o f ) o e = e o f o e
Ce sont deux sandwiches. Appelons-les :
p = e o ( e o f )
q = e o f o e
...Selon l'axiome du sandwich, on peut "extraire le jambon", c'est à dire calculer les expressions de ( e o f ) et f de qui seront égales, puisque p = q. Donc :
( e o f ) = f
...Recommençons en partant de la propositions attribuée à ce deuxième éléments f :
f o f = f
...Multiplions à droite par e, deux fois à gauche :
e o f o f = e o f
e o e o f o f = e o e o f
...Utilisons l'associativité :
e o ( e o f ) o f = e o e o f
...En utilisant une seconde fois l'axiome du sandwich on en déduit que :
e o f = e
donc :
e = f
Théorème III : Si je prends cet élément e "identique à son carré", il entraîne que
a o e = a
Démonstration :
On utilise toujours l'axiome du sandwich. On part de la définition de e :
e o e = e
on multiplie à droite successivement par a et par e :
e o e o a o e = e o a o e
On fait jouer l'associativité.
e o ( e o a ) o e = e o a o e
Donc :
e o a = a
En repartant de :
e o e = e
et en multipliant à gauche successivement par a et e :
e o a o e o e = e o a o e
et en faisant jouer l'associativité.
e o ( a o e ) o e = e o a o e
d'où :
a o e = a
Le théorème III est démontré.
Passons au théorème IV
(existence d'un réciproque, noté a-1).
Enoncé : soit un élément de l'ensemble. Il existe un élément et un seul, solution de l'équation :
a o y o a = a
Nous noterons cet élément a-1 et nous l'appellerons réciproque de a. Cet élément satisfait les propriétés :
a o a-1 = e
a-1 o a = e
Démonstration.
L'existence et l'unicité de cet élément est une simple conséquences de l'axiome du sandwich, lorsqu'il se formule ainsi :
Lorsque les tranches de pain sont identiques entre elles et identiques au sandwich, alors le jambon est le réciproque de la tranche de pain (ou du sandwich).
a o y o a = a
Nous pouvons faire jouer l'associativité de deux façons :
( a o y ) o a = a
a o ( y o a ) = a
Or nous savons que :
e o a = a
a o e = a
Donc la solution y satisfait :
a o y = e
y o a = e
Montrons que cette solution est unique. Si elle ne l'était pas, on en aurait une autre
a o z = e
z o a = e
Multiplions la première équation par y à gauche.
y o a o z = y o e
( y o a ) o z = y
mais y o a = e donc :
z = y
On appelle cette solution a-1 , solution de l'unique équation :
a o a-1 o a = a
Ainsi le nouveau jeu d'axiomes conduit aux mêmes propriétés qui, classiquement, définissent les groupes.
On peut donc définir les groupes à l'aide de ce nouveau jeu d'axiomes :
Définition d'un groupe.
1 - Il existe des éléments a , b , c ... appartenant à un ensemble E
2 - Il existe une opération interne, notée o ("rond"), permettant de combiner deux éléments d'un ensemble.
a appartient à l'ensemble E
b appartient à l'ensemble E
a o b appartient à l'ensemble E
3 - Cette opération est associative :
a o b o c = ( a o b ) o c = a o ( b o c )
4 - Soient trois éléments a , b , c , appartenant à l'ensemble E.
Soit l'équation :
a o y o b = c
Elle possède une solution unique.
Si les éléments de l'ensemble E, muni de son opération de composition interne, satisfont ces quatre axiomes, je dis qu'ils forment un groupe.
Théorème : L'élément neutre est son propre réciproque. Cette nouvelle définition de l'élément neutre, à l'aide d'une seule équation, engendre un autre type de démonstration de cette propriété.
e o e = e
C'est la définition de l'élément particulier e. Or l'axiome du sandwich fait que cette équation s'identifie avec la propriété (et non plus la définition) du réciproque.
Autre théorème : le réciproque du réciproque est égal à l'élément lui-même :
(a-1)-1 = a
a-1 o a = e
a o a-1 = e
a est l'inverse de a-1. D'où la propriété.
Montrons que :
( a o b )-1 = b-1 o a-1
On calcule :
a o b o b-1 o a-1 et b-1o a-1 o a o b o
Montrons que ces deux quantités sont égales à e.
a o (b o b-1 ) o a-1
= a o e o a-1
= a o a-1
= e
Idem pour l'autre expression.
- C'est une approche différente du concept de groupe.
- L'ontologie des groupes.
- Si tu veux.
- Mais quelque chose me dit que ce truc a s'avérer fécond.
- Maintenant, oublie tout, y compris l'axiome du sandwich. Considérons un ensemble E muni d'une opération de composition interne o associative. Supposons que dans cet ensemble il existe un élément qui, composé avec tous les autres, joue le rôle d'élément neutre :
a o e = e o a = a
- Il est unique ?
- S'il existe, il est nécessairement unique, ça se démontre.
- Ah oui, c'est vrai..
- Je dirai que deux éléments a et b seront liés par une relation de réciprocité si
a o b = b o a = e
Si on se donne a , b est son réciproque. Je dis que si je limite l'ensemble au sous-ensemble des éléments qui possèdent un réciproque, ce sous-ensemble forme un groupe. C'est une façon de construire des groupes. Autrement dit, on sélectionne dans l'ensemble, les éléments qui satisfont à cette propriété et je dis que cela suffit pour affirmer que ce sous-ensemble forme un groupe.
Il faut montrer que cette propriété est interne.
- Que veux-tu dire ?
- Soit deux éléments a et a' satisfaisant la propriété, c'est à dire :
a o b = b o a = e
a' o b' = b' o a' = e
a possède un réciproque b
a' possède un réciproque b'. Ils sont donc dans le sous-ensemble en question. Il faut montrer que a o a' possède également un réciproque.
Enlevons ces "ronds", qui sont lourds.
a'h' = e
multiplions à gauche par a et à droite par b :
a a'b'b = a e b = a b = e
Donc :
(a a' ) (b'b ) = e
Repartons de :
b a = e
multiplions à gauche par b' et à droite par a' :
b'b a a'= b' e a' = b'a' = e
( b'b)( a a' ) = e
Donc l'élément obtenu en composant a et a', qui possèdent des réciproques, possède lui aussi un réciproque.
- Reste à montrer que ce sous ensemble forme bien un groupe.
- Et pour cela, je vais montrer que ce sous ensemble satisfait l'axiome du sandwich, c'est à dire que :
a y b = c
a une solution y unique.
- Je comprends. Axiomatiquement, tu procèdes à l'inverse de tout à l'heure. Plus on haut tu t'étais donné l'axiome du sandwich et tu avais montré que ceci entraînant l'existence de réciproques. Là tu supposes que les éléments de l'ensemble ont tous des réciproques et tu vas te débrouiller, en utilisant cette propriété, pour retrouver l'axiome du sandwich.
- La meilleure façon de montrer que l'équation possède une solution unique est de la construire. Multiplions l'équation ci-dessus à gauche par a-1 et à droite par b-1.
a-1 a y b b-1= a-1 c b-1
( a-1 a ) y ( b b-1) = a-1 c b-1
y = a-1 c b-1
- Ainsi y est bien solution de l'équation :
a y b = c
En introduisant la solution construite, il vient :
a ( a-1 c b-1) b = c
...Ce faisant on admet qu'on peut jouer avec les parenthèses, généraliser l'associativité. On a supposé (c'est un des axiomes) qu'on pouvait isoler deux éléments dans une séquence d'opérations
a o b o ( c o d ) a o ( b o c ) o d ( a o b ) o c o d ( a o b) o ( c o d )
Il s'agit de montrer qu'il est licite d'inclure trois éléments entre deux parenthèses. Mais nous admettrons ceci sans démonstration.
Applications :
...Considérons l'ensemble des réels doté de la multiplication x comme opération de composition. Elle est interne, mais ça n'est pas un groupe, en vertu de ce nouveau lot d'axiomes. En effet l'équation qui définit l'élément e :
e o e = e
a deux solutions :
e = +1 et e = -1
...Considérons la construction précédente. On se donne un ensemble (les réels), une opération de composition, associative (la multiplication). Cet ensemble possède un élément neutre 1 , qui n'est alors pas défini en tant que solution de
e o e = e
mais en tant qu'élément qui, se composant avec tout autre élément du groupe (y compris lui-même), redonne celui-ci, autrement dit la définition classique :
Pour tout a appartenant à l'ensemble E il est vrai que :
e o a = a o e = a
Si on part de la définition classique du réciproque :
a o a-1 = a-1 o a = e
...Nous avons montré que le sous ensemble des éléments possédant un réciproque constituait un groupe. Ainsi les réels moins le zéro constituent un groupe.
Prenons les matrices carrées de format (n,n) Elle possèdent un élément neutre :
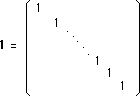
avec des zéros en dehors de la diagonale principale, peuplée de " 1 "
Les matrices inversibles forment un groupe, qu'on appelle le Groupe Linéaire GL(n).
- Moi ça me plaît bien, tout cela.
- Hmmm.... ça n'est qu'une variante de l'axiomatique classique. J'ai présenté cela à un colloque d'épistémologie, à Grenoble, il y a une semaine.
A SUIVRE
