Le Retournement de la Sphère
7 décembre 2004
page 1
Introduction.
On considèrera dans ce qui va suivre des surfaces fermées, comme la sphère, le tore et quelques autres. Ce sont des surfaces au sens où l'entend l'homme de la rue, c'est à dire que ce sont des objets à 2 dimensions qu'on représente dans un espace euclidien à trois dimensions, R3, qui est notre espace mental de représentation. Ces surfaces peuvent faire l'objet de plusieurs types de représentations. Si elles ne se recoupent pas elles-même, on dira qu'elles sont plongées (dans R3). Si elle se recoupent on parlera alors d'immersions et ce recoupement se traduira alors par la présence d'un ensemble d'auto-intersection (self-intersection).
Dans nos plongements on supposera que le plan tangent varie continûment et que la surface est exemple de singularités comme pourrait l'être par exemple le sommet d'un cône. Nos surfaces seront régulières.
Dans le cas des immersions on demandera alors à ce que le long des lignes d'auto-intersection les deux plans tangents aux nappes qui se croisent soient distincts.
Le monde la géométrie, tel que le conçoit le mathématicien, est assez différent du monde physique. Le fait que les surfaces puisse s'auto-traverser ne le gêne nullement. Le monde physique ne permet pas ce genre de chose. Mais cela devient possible dans le monde métaphysique. Ainsi dans la Bible on lit que lorsque les morts ressusciteront, cela sera sous la forme de "corps glorieux". Ils pourront alors passer au travers de n'importe quoi et en principe seront capables de se traverser eux-mêmes. Ainsi, quand le temps du Jugement Dernier sera venu, si vous baladez dans Rome sous forme de corps glorieux, que vous êtes perdu et que vous cherchiez la piazza Navona, vous pourrez être tenté de demander votre chemin à un autre mortel ressuscité, ayant la même apparence que vous. Supposons que la personne que vous interrogez se dirige dans la direction opposée par rapport à cette place. Dans l'espace physique ordinaire, pour vous indiquer le bon chemin il lui faudrait pivoter sur lui-même pour pointer son doit dans cette direction. Mais s'il chemine sous forme de corps glorieux, cette rotation ne sera plus nécessaire. Il pourra pointer son index sur son nombril et se traverser lui-même. Lorsque sa main réapparaîtra en émergeant de son dos il ne lui restera plus qu'à vous dire "c'est par là". En enfonçant son bras au travers de son ventre il aura créé dans son enveloppe corporelle un ensemble d'auto-intersection constitué par deux cercles, qui disparaîtra lorsqu'il reprendra sa configuration normale.
Si un être humain ferme la bouche, met une pince à linge sur ses narines pour les obturer et qu'on fait abstraction de ses autres orifices naturels son enveloppe corporelle adopte alors la topologie de la sphère S2. Imaginons un être ressuscité sous forme de corps glorieux dont les orifices naturels seraient ainsi obturés. Nous savons qu'il peut se traverser lui-même, c'est à dire que son enveloppe corporelle peut passer d'une situation de plongement à une situation d'immersion. Un des problèmes métaphysique qui s'est alors posé a été de savoir si un bonhomme resuscité sous forme de corps glorieux pouvait se retourner dans faire de plis.
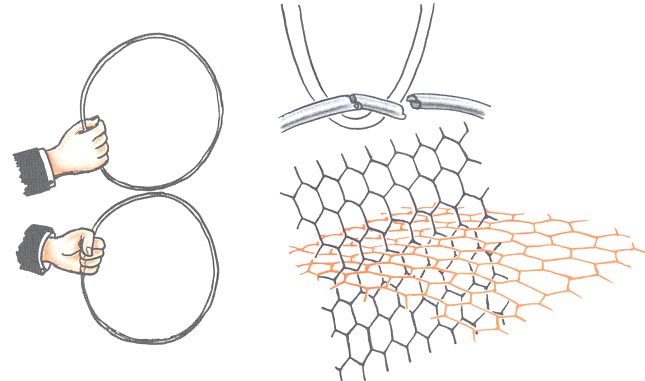
Une petite remarque en passant. Les prestidigitateurs savent utiliser des "cercles magiques" qui peuvent s'interpénétrer "de façon magique". On pourrait imaginer de représenter des surfaces à l'aide d'une sorte de "grillage magique" tels que les deux nappes, représentées ici l'une en noir et l'autre en rose, puissent se traverser dans difficulté.

Le grillage magique
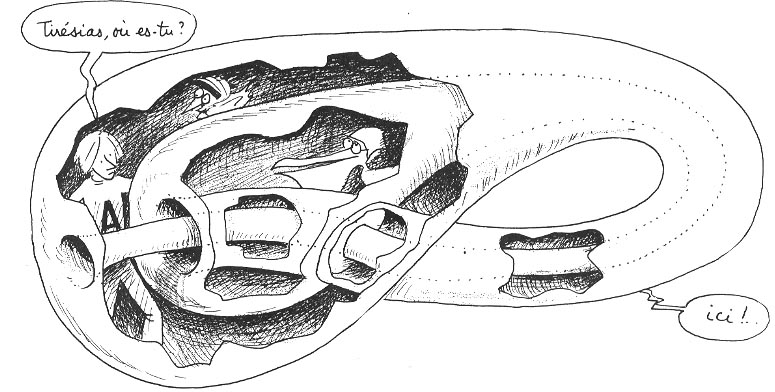
De toute façon, il faut convenir qu'ils n'y a souvent pas beaucoup de différence entre les mathématiques et la magie. J'ai conçu il y a vingt ans une bande dessinée : le Topologicon. Elle est maintenant épuisée et introuvable, sauf sous forme d'objet de collection. Sur l'une des pages on pouvait voir ceci :
![]()
Il est bien dommage que les éditions Belin aient décidé d'abandonner cette collection. Il faut dire qu'avec un prix de fabrication d'à peine plus d'un euros, vendre les albums 13 euros (plus le port), en vente par correspondance, en dehors du fait que cela laissait une marge bénéficiaire de 12 euros, c'est à dire avec un bénéfice dépassant 92 pour cent du prix de vente, ne correspond pas à une stratégie commerciale très évidente, surtout pour du noir et blanc.
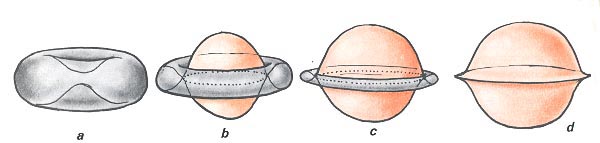
Considérons une sphère S2 plongée dans R3. Nous supposons que sa surface extérieure est grise et que son intérieur a une couleur vieux rose. Nous pouvons appuyer sur deux points antipodaux, que nous appellerions arbitraitement "pôle nord" et "pôle sud", jusqu'à les mettre en contact selon un point. On peut faire ça par exemple avec un beignet. Quand il s'agit d'un beignet mathématique (on ne sait pas si les beignets ressuscitent ou non sous forme de corps glorieux) les deux régions polaires, après avoir été en contact selon un point, peuvent s'auto-traverser selon une courbe d'auto-intersection qui affecte la forme d'un cercle. En anticipant, nous dirons que cette surface à subi une catastrophe de type Do.
On peut alors être tenté d'essayer de retourner le beignet, la sphère, en poursuivant l'opération. Mais alors un bourrelet va se former, qui va dégénérer selon un vilain pli, ou plus exacterment une surface de rebroussement (figure d). .
A la fin des années cinquante la grave question de savoir si on pouvait retourner des beignets métaphysiques sans faire de plis restait non résolue. A dire vrai, tout le monde pensait que cela était strictement impossible. Mais en 1957 un mathématicien, Stephen Smale (qui reçut la médaille Field mais pour un tout autre travail ) démontra que les différentes immersions de la sphère S2 dans R3 constituaient un unique ensemble et qu'il était toujours possible de trouver une suite de déformations continues d'immersions (qu'on appelle aussi homotopie régulière) permettant de passer d'une situation à une autre. Le corollaire était qu'on devait pouvoir passer à l'aide d'une suite continue d'immersion du plongement standard de la sphère S2 au plongement antipodal. Dit en termes plus simples : on devait pouvoir retourner une sphère sans faire de plis, à condition de lui permettre de se retourner elle-même.
Le patron de Smale s'appelait Raoul Bott. Celui-ci demanda à son élève comment on devait s'y prendre et Smale répondit qu'il n'en avait pas la moindre idée, mais que son théorème était totalement inattaquable. Smale ne voyait pas du tout dans l'espace mais il n'en avait cure (comme c'est le cas chez beaucoup de géomètres). Et, si on est tout à fait franc, après avoir démontré son théorème il se moquait éperduement de la façon dont on pourrait s'y prendre pour concrétiser la chose et s'était empressé de s'intéresser à un autre sujet, laissant ses collègues mathématiciens dans la plus grande perplexité. je trouve que ça n'est pas très sympa de créer comme ça des problème et de laisser ensuite les gens se débrouiller pour trouver la solution, dix ans après.
Il faut dire qu'il est assez difficile d'imaginer des immersions, dans sa tête. Pourtant on connaît des surface qui ne peuvent être représentées dans R3 que de cette façon. La bouteille de Klein, par exemple.
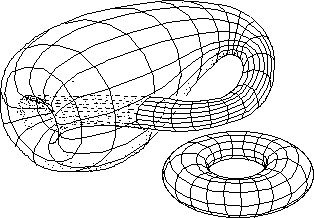
Bouteille de Klein
On l'a représentée ici avec un système de maillage-système de coordonnées constitué par deux ensembles de courbes fermées, comme le tore. On peut ainsi mailler une bouteille de Klein sans créer de singularité de maillage. Mais comme on peut le voir cette surface s'auto-traverse nécessairement selon une courbe fermée, un cercle. On ne peut donc pas plonger une bouteille de Klein dans R3. J'ai essayé, ça ne marchepas. On ne peut que l'immerger. Grâce à mes talents de dessinateur vous arrivez à peu près à vous représenter cet objet. Mais quand il s'est agi de retourner une sphère il a fallu envisager des configurations beaucoup plus compliquées. La façon de les représenter n'était pas des plus commodes. Certains utilisaient de la pâte à modeler. Quand on les voyait discuter entre eux dans des colloques, ils se mettaient généralement à l'écart, et ouvrait devant leurs collègues des boites à chaussures ou des cartons à chapeaux, contenant des objets plus ou moins monstrueux. Le dessin ci-dessus évoque la façon la plus commode de construire ces objets et de les manipuler : avec ce qu'on appelle du "fil de fer cuivré", un alliage qui est assez souple pour que l'on puisse le plier sans difficulté, mais qui conserve néanmoins son élasticité. La meilleure façon de procéder consiste alors à matérialiser les point de rencontre des lignes (nous recommandons des tiges de 2 mm de diamètre) en les fixant à l'aide de ligatures de fil. L'avantage est qu'on peut les faire glisser, du moins jusqu'à ce qu'on considère que l'objet a acquis une forme définitive. On peut alors supprimer tout glissement à l'aide d'un point de colle.
Dans la pratique il est assez rare qu'on ait à se servire de bouteilles de Klein. Ci-après, une photographie d'une bouteille de Klein que j'utilise pour mes besoins personnels.

Ces objets, pour peu qu'on ait quelque sens des formes, sont assez beaux. J'en ai fait construire un certain nombre quand j'étais professeur de sculpture à l'Ecole des Beaux-Arts d'Aix en Provence Mais avant que je ne passe à cette technique il y eut bien des tâtonnements où nous mélangions le fil de fer mou et le carton, ce qui donnait des résultats d'une esthétique tout à fait discutable. Je me rappelle qu'un jour j'avais du prendre le train à Marseille pour amener à Paris à mon regretté ami le mathématicien André Lichnérowicz plusieurs surfaces dont j'avais réussi à construire des représentations sufisamment parlantes. Il y avait en particulier la surface de Boy où j'avais plaqué une cartographie centré sur un pôle unique. Cela a donné à la fin un objet absolument superbe, qui fut exposé pendant vingt ans dans la salle pi du Palais de la Découverte de Paris. Mais il y a un an la direction du Musée estima que cette surface était passée de mode et elle repose maintenant dans un grenier ou dans une cave. J'espère qu'elle n'a pas été écrasée dans le transport. Tout cela pour dire que vous ne pourrez maintenant voir de surface de Boy nulle part, sinon dans des livres, ou dans un CD ROM sur lequel j'ai consigné mes 18 bandes dessinées scientifiques en format pdf, dont le Topologicon. Comment se procurer ce CD-rom.
Mais revenons à ce voyage que j'avais entrepris, de Marseille à Paris. J'étais déjà encombré par deux valises et j'avais décidé de prendre avec moi trois modèles. La seule solution avait été de les accrocher autour de mon cou. Mais quand j'ai traversé le hall de la gare et que j'ai vu comment les gens me regardaient j'ai compris qu'ils s'imaginaient avoir affaire à un fou qui avait obtenu de son asile une permission de sortie. Il aurait été totalement vain de tenter de leur expliquer le contraire et j'ai du subir ce calvaire avec toute la dignité possible.
Ce qui est amusant c'est que les gens qui construisent des choses de ce genre sont assez rares. Il y avait en Amérique un mathématicien nommé Charles Pugh, qui travaillait au département de mathématiques de l'université de Berkeley. J'aurai l'occasion de reparler de lui par la suite. Pugh était absolument génial avec le grillage pour les poules, mais personnellement j'ai toujours préféré la technique du fil de fer cuivré.
Revenons à cette histoire de retournement de sphère. Le premier qui réussit à venir à bout de ce problème fut le géomètre Anthony Phillips Il publia son travail, c'est à dire une suite de dessins dans un numéro de Scientific Americain, en 1967. Il y a plusieurs façons de retourner une sphère. L'une consiste à amener chaque point de la sphère en coïncidence avec son antipode. Elle prend alors la forme d'une surface de Boy. J'ai toujours rêvé de trouver un sponsor pour construire une magnifique sculpture qui représenterait un globe terrestre qui serait replié en surface de Boy. Faute de pouvoir construire l'objet j'en ai fait l'illustration de couverture du Topologicon :
![]()
La sphère terrestre recollée sur elle-même selon une surface de Boy
Dans une telle configuration, si on creuse un trou au pôle nord on émerge aussitôt de l'autre côté, au pôle sud, puisque ces deux points sont antipodaux. Un Français qui creuserait un trou dans sa cave se retrouverait en Nouvelle Zélande, etc.
La version trouvée par Anthony Phillips consiste effectivement à décrire la façon dont la sphère se configure en forme de revêtement à deux feuillets de la surface de Boy, qui est bien entendu une surface unilatère. Si on disposait d'un produit magique, la traversine, qui donnerait aux surfaces le don de pouvoir se traverser elles-mêmes, il suffirait de joindre chaque à son antipode par un fil, qu'on ferait se rétrécir jusqu'à devenir de longueur nulle. Si on ne peut pas aisément représenter cette transformation on peut néanmoins s'intéresser à une partie de la sphère, par exemple son voisinage équatorial. C''est ce qui a été fait dans les animations qui suivent. Cette surface, dotée de deux bords circulaires ressemble à une jante de roue de bicyclette. On a figuré trois rayons, reliés aux points diamétralement opposés. En faisant tendre la longueur de ces rayons vers zéro cette bande bilatère se configurera en revêtement à deux feuillets d'un ruban de Moebius à trois demi-tours. Ci-après, deux animations assez grossières. celle de gauche est lente et celle de droite rapide.
 |
 |
Ce ruban de Moebius à trois demi-tours est le "voisinage équatorial" de la surface de Boy. C'est sur cette bande que vient s'enrouler l'équateur de la sphère.
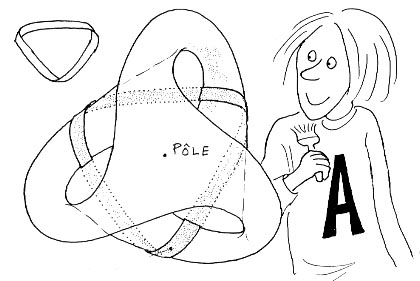
" L'équateur " de la surface de Boy
Quant aux deux pôles de la sphère ils viennent en coïncidence sur le pôle unique de la surface. Celle-ci, comme la bouteille de Klein, ne peut être plongée dans R3. Elle ne peut qu'être représentée sous forme d'une immersion. Elle possède alors un ensemble d'auto-intersection qui a la forme d'une hélice à trois pales dont on aperçoit des extrémité, qui ressemblent aux "tympans" de trois "oreilles". Dans les planches suivantes on trouvera quelques éléments pour mieux "lire" cette surface. En cas de problème, procurez-vous un Topologicon.
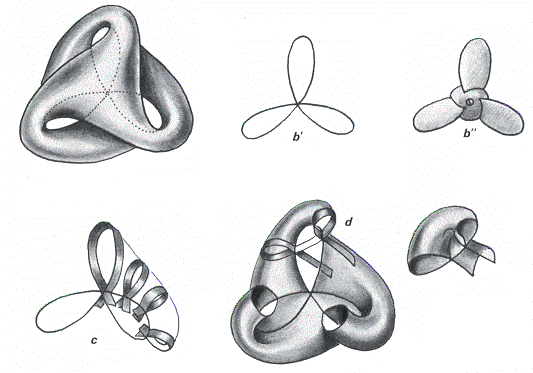
En haut et à gauche une surface de Boy. Comme cette surface est unilatère ont ne saurait utiliser deux couleurs. En b' l'ensemble d'auto-intersection, trifolié, évoquant les pales d'une hélice en b". La courbe se recoupe en un point triple T. Les dessins suivants sont là pour aider le lecteur à s'y retrouver.
Tout est bon pour tenter d'illustrer la structure d'une surface : des bandelettes, un montage avec des pièces rapportées. On voit qu'un sculpteur trouverait son bonheur avec cet objet réellement fascinant. Un mot au passage sur son histoire. En 1901 un étudiant du grand mathématicien allemand Hilbert, Werner Boy, évoqua devant lui une surface dont personne n'avait eu l'idée auparavant. Les vacances étaient toutes proches. Hilbert dit à son étudiant :
- Ce problème me paraît intéressant. Si vous voulez, revenez me voir à la rentrée, nous en discuterons.
Les vacances passèrent, mais à la rentrée Boy ne réapparut pas. Au bout de deux mois, Hilbert esseya de le trouver. D'autres étudiants lui ayant signalé son adresse, il s'y rendit. Mais la logeuse lui déclara que le jeune Werner Boy lui avait rendu les clés avant l'été et qu'il n'était plus réapparu. Toutes les recherches menées pour le retrouver s'avérèrent vaines, de même que celles de retrouver des membres de sa famille. Il se volatilisa littéralement. Si vous vous rendez en Allemagne, n'espérez pas vous rendre sur la tombe de cet illustre inventeur : elle n'existe pas.
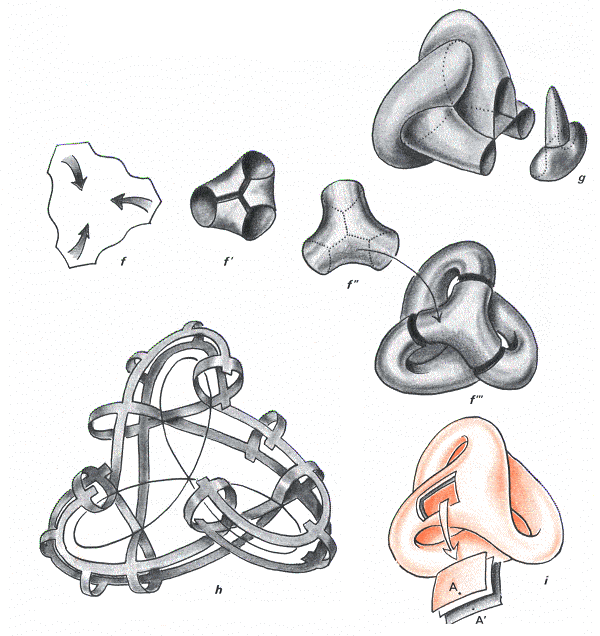
Sur la dernière figure, en bas et à droite, on a fait figurer, en blanc, la surface de Boy proprement dite et avec des couleurs grises et roses les deux côtés de la sphère qui la revêt. Les points A et A' sont, sur cette sphère, antipodaux. On comprend en tout cas comment ce revêtement à deux feuillets de la surface de Boy peut être utilisé pour retourner la sphère. Supposons que nous disposions de la suite de transformations, de l'homotopie régulière qui ait permis de transformer une sphère rose à l'extérieur, grise à l'intérieur en cette figure en bas et à droite. Il suffirait alors d'échanger les deux nappes (en les faisant s'auto-traverser), entre autre les points A et A' et d'opérer les mêmes transformations, effectuées à rebours, pour tomber sur le plongement antipodal de cette sphère, présentant cette fois sa couleur grise à l'extérieur.
Dans la même logique on peut s'attendre à ce qu'un tore puisse se configurer en revêtement à deux feuillets d'une ... bouteille de Klein. Voici à quoi ressemble ce revêtement.
Revêtement à deux feuillets de la bouteille de Klein
Si on parvient à configurer un tore de cette façon il suffit encore une fois d'échanger les nappes adjacentes, situées de part et d'autres de la bouteille de Klein (non représentée ici), puis d'opérer les opérations en sens inverse pour tomber sur le tore retourné. Ce travail a été présenté dans le numéro de janvier 1979 de Pour la Science dans un article signé B. Morin et J.P.Petit. Je me suis chargé de la partie dessine et Morin du texte. Bien qu'il ait cité beaucoup de monde dans ce papier, il m'a oublié au passage, comme il a oublié de mentionner que j'étais l'inventeur de cette partie du travail, présenté sur les pages 46 et 47. Mais ce sont des choses qui arrivent quand on collabore étroitement avec un collègue. Vous savez comment c'est : on est tellement habitué à sa présence depuis des années et on est tellement soucieux de n'oublier personne qu'on finit par l'oublier lui, comme s'il faisait partie du mobilier. Pour plus de détails ce travail a été publié sous mon nom aux Comptes Rendus de l'Académie des Sciences de Paris le 20 novembre 1978, sous le titre "Retournement non-trivial du tore", l'article ayant été présenté par l'Académicien André Lichnérowicz.
Retour vers Nouveautés Retour vers Guide Retour vers la page d'Accueil
Nombre de consultations de cette page depuis le 7 décembre 2004 :