Come trasformare una superficie Cross Cap

in una superficie di Boy (destra o sinistra, a scelta)

passando per la superficie romana di Steiner.

Italiano : Andrea Sambusetti, università di Roma

27 settembre - 25 ottobre 2003

pagina 2

Ecco una "superficie Cross Cap" (così some l'avreste scoperta nelle immagini di realtà virtuale). Essa presenta due punti cuspidali che sono vertici di una linea di autointersezione. La si può costruire pizzicando un palloncino con delle mollette per bigodini. Ma potete anche costruirne delle rappresentazioni poliedriche. Quella in basso ci interesserà particolarmente.

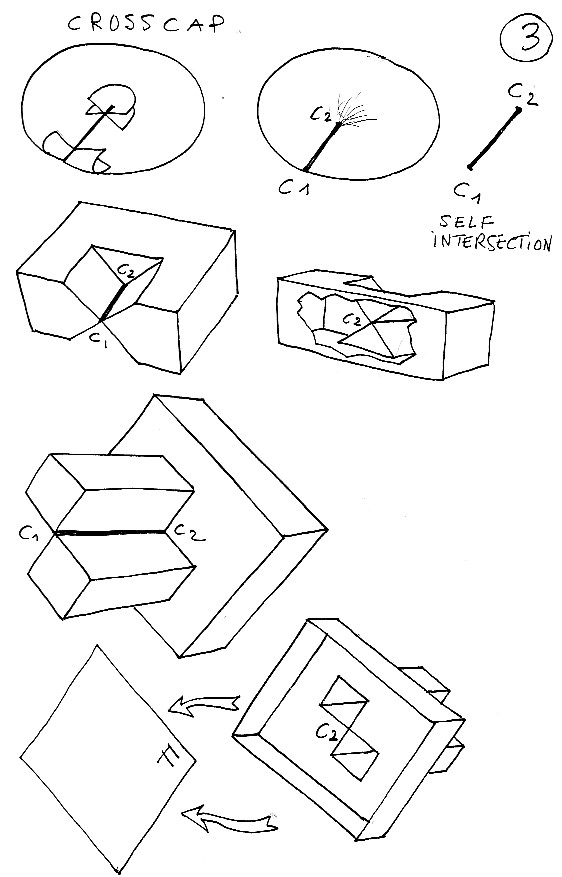
Nella tavola 4 si trova la cosa più difficile da imparare. Mi sembra impossibile che qualcuno capisca bene questi oggetti semplicemente guardando le figure. Costruite dei modellini. In parole povere, si tira il punto cuspidale C₂ verso "l'interno della superficie" (il che, tra parentesi, non ha alcun senso poiché, l'avrete senz'altro notato subito, la superficie Cross Cap è unilatera: non ha una faccia esterna ed una interna). Insistendo, la superficie si "auto-attraversa", e l'insieme di autointersezione si completa, arrotondando un po' le cose, con una curva a forma di 8. Si è creato, per inciso, un punto triplo T.

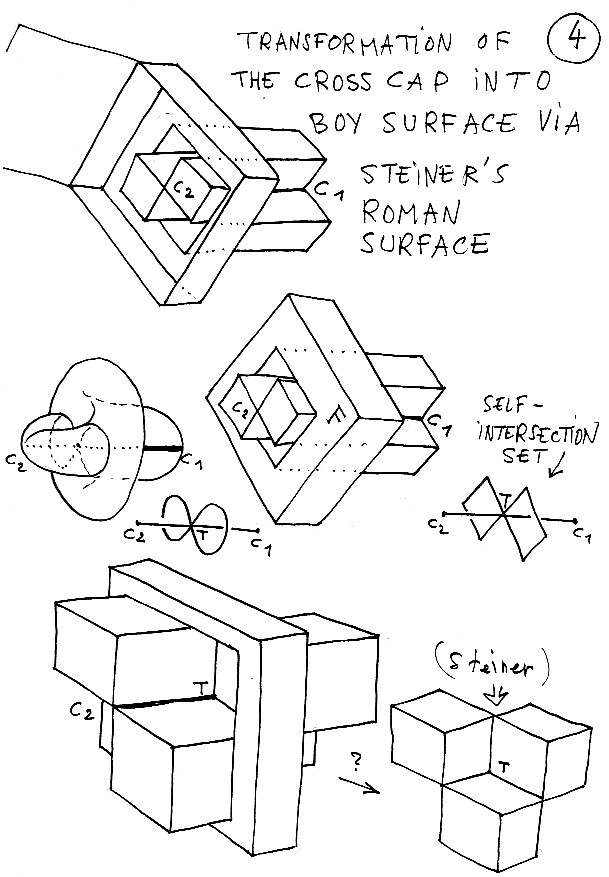
La superficie risulta più comprensibile nella sua forma poliedrica e, in basso, abbiamo ingrandito certi elementi per mostrare ciò che ci induce a trasformare questo oggetto in superficie romana di Steiner (si veda la simulazione di realtà virtuale) la cui forma poliedrica più semplice consiste nell'assemblare quattro cubi (qui se ne vedono solo tre).

Tavola 5 : versione poliedrica a sinistra, tonda a destra. La freccia passa per il punto che andiamo a "strozzare". Più in basso, l'inizio dell'operazione di strozzamento.

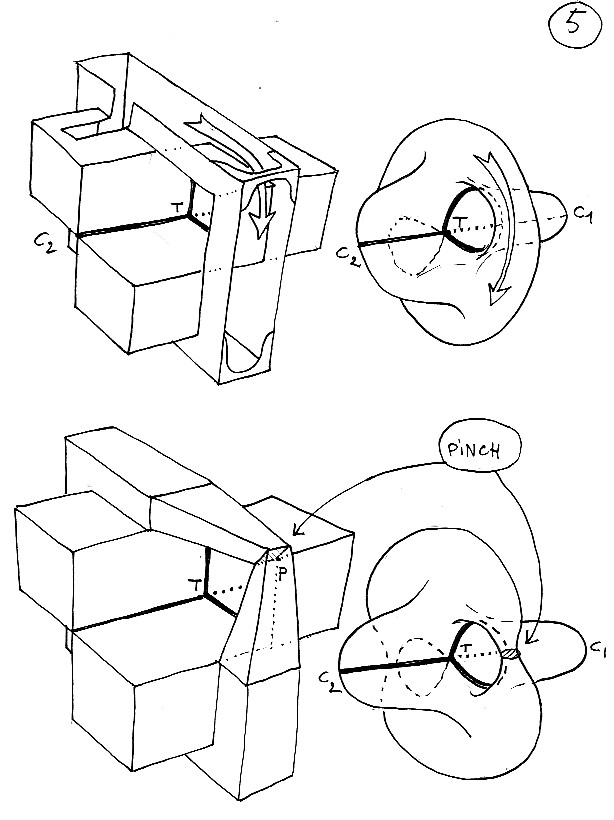
Tavola 6 : lo strozzamento viene effettuato e crea un punto singolare B. In effetti, dal momento che la strozziamo da entrambe le parti (tanto per risparmiare tempo), si formano due punti singolari S1 e S1, poi due punti cuspidali. A questo punto, senza cartoncino bristol, forbici e nastro adesivo, siete messi male.

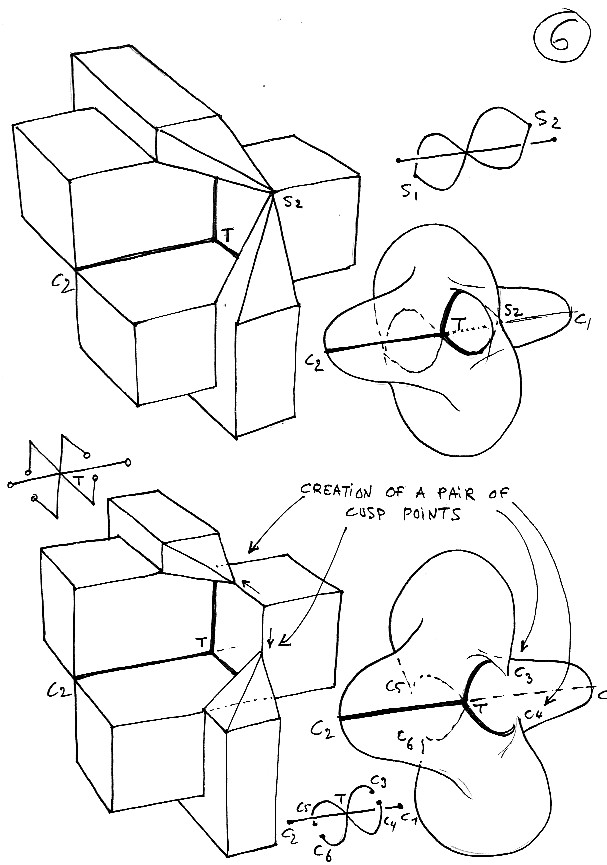
Tavola 7 : qui abbiamo semplicemente fatto migrare i differenti punti cuspidali. Se il punto C2 è "evidente", avrete sicuramente più difficoltà invece a identificare i punti C3 e C4 come cuspidali. Eppure sono lì, alle estremità di una linea di autointersezione. Al di sopra del punto C3 si trova semplicemente quello che ho chiamato un "posicono", un punto, cioè, in cui si concentra della curvatura positiva (un punto in cui si concentra della curvatura negativa lo chiamo "negacono"). Deformando un pochettino questo oggetto, si arriva alla forma poliedrica della superficie romana di Steiner (inventata da Steiner a Roma; si veda la sua illustrazione in realtà virtuale).

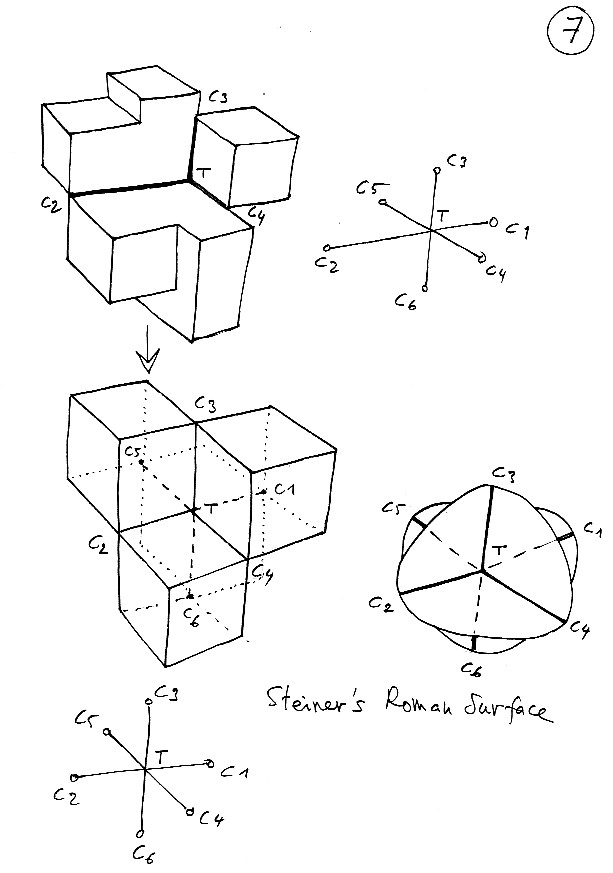
Dunque il gioco è fatto. Esistono vari tipi di superfici, secondo le regole che uno impone. Le superfici che non si autointersecano sono dette "embeddings" (della sfera, o del toro in  R3). Quando invece si autointersecano ma il piano tangente varia in modo continuo senza degenerare, sono dette immersioni. Per esempio : la bottiglia di Klein, nella sua rappresentazione classica. In R3 non esiste una rappresentazione della bottiglia di Klein sotto forma di embedding: si autointerseca necessariamente. Le immersioni possiedono degli insiemi di autointersezione senza punti cuspidali. Questi insiemi sono curve continue, ma possono incrociarsi in punti doppi o tripli. Osservazione: la sfera si può realizzare sotto forma di immersione (che non è un embedding) facendola autointersecare. E' in effetti il modo attraverso il quale si riesce a rovesciarla (cf. il metodo di A.Phillips, 1967, che ha come passo centrale il rivestimento doppio di una superficie di Boy; e si veda anche B.Morin e J.P.Petit, 1979, in cui si prende come modello centrale il modello "a quattro orecchie" di Morin, di cui qui sotto vedete una rappresentazione poliedrica che ho inventato una decina di anni fa).

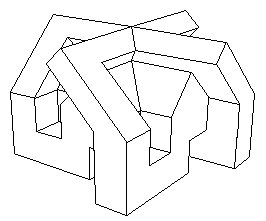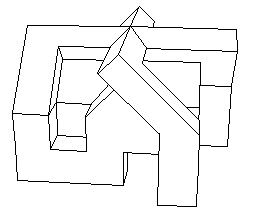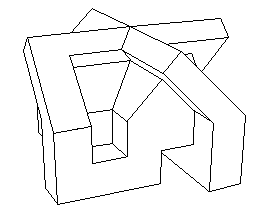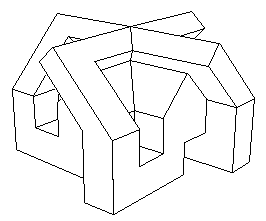
Piano di montaggio di questo oggetto con carta e forbici

Se si estendono le regole di gioco accettando che questi oggetti ammettano anche dei punti cuspidali, si ottengono delle summersioni (la Cross Cap, la superficie romana di Steiner). Non so se summersione sia il termine sia giusto, ma dato che non ho trovato alcun matematico che mi possa chiarire le idee al riguardo, ho trovato divertente inventarmene uno, provvisoriamente, almeno finché un geometra esperto si farà avanti. Così, la superficie Cross Cap e la superficie romana di Steiner sarebbero delle summersioni del "piano proiettivo".

Per dirvela tutta, dopo venticinque anni di attività e le mie delusioni in materia di Magneto-Idrodinamica, avevo iniziato questi lavori perché mi sembravano i più lontani possibile da qualsiasi applicazione militare. Ma, come mi fece notare il mio vecchio amico Mihn, il termine summersione potrebbe prestarsi a confusione e lasciar intendere alla Marina Militare che attraverso queste ricerche io proverei a nascondere dei progressi in materia di propulsione sottomarina.

La regola di "creazione-scioglimento" di coppie di punti cuspidali permette di passare da una summersione di un oggetto ad un'altra, ed è quello che abbiamo appena fatto, mostrando che la Cross Cap e la superficie romana di Steiner sono due summersioni dello stesso oggetto, noto come piano proiettivo. Non cercate di figurarvi un "piano proiettivo". Questo oggetto si può comprendere solo attraverso varie rappresentazioni differenti. Quanto al termine "proiettivo", non è che uno tra i mille inventati dai matematici per sviare coloro che vorrebbero penetrare nel loro circolo chiuso. Lo Zanichelli non vi sarà di alcuna utilità in matematica.

Ci resta quindi da vedere come passare alla superficie di Boy, che è un'immersione del piano proiettivo

Pagina precedente                  Pagina seguente

Torna all'indice "Trasformazione di una Cross Cap in Boy "

Torna alla sezione Novità            Torna alla sezione Guida           Torna alla Pagina Principale

Numero di visite dal 25 ottobre 2003 :