Jean-Pierre Petit

Lambda Laboratory

...In the section devoted to MHD we have seen that it could be possible, using disk-shaped MHD aerodyne, to cruise at hypersonic velocity, at low altitude, without creating sonic bang and turbulence, a completely noiseless flight.

...Second question : is interstellar travel possible ?

...Classical answer : no, due to the contrainsts of special relativity.

...A solution suggested by O'Neill : men could travel to other stars if they accept that only their distant descents could reach these other systems. If should be a one-way journey, without possible return, which implies huge spacecrafts, as big as large terrestrial towns, carrying grass, trees, animals everything. The modern version of Noe's ship. Source of energie : the hydrogen picked on way, combined to fusion process. Source of materials : asteroids.

...Poetic....

...Of course : no possibility to talk with men who stay on the Earth. I am skeptical. More, I think that if we would build such a monster and take place in, when reaching another distant planet, circling around another star and inhabited by human creature, when landing, these guys would say :

- Glad to meet you. We expected you. Your descents warned us twenty thousands years ago. You know, they are more modern way to travel, now.

...I wouldn't take the risk to be so ridiculous. So, can we think about something fairly different ?

...The reader may have a look to the papers of my website, devoted to theoretical cosmology. Recent works will be presented in Marseille, France, june 2001, at the international meeting on astrophysics and cosmology, entitled "Where is the matter ?", organized by the Laboratoire d'Astrophysique de Marseille (I belong to).

1 - Twin universe geometry.

...The concept of twin universe was first introduced by Andrei Sakharov, in 1967 ( [1] , [2] , [3] , [4] ). Later I published two papers in the french Comptes Rendus de l'Académie des Sciences de Paris ( [5] and [6], unaware previous Sakharov's works). The underlying geometric structure corresponds to a two-points bundle. Give the fold of this bundle the metric structure ( g , g*), where g and g* are riemanian metrics with signatures ( + - - - ).

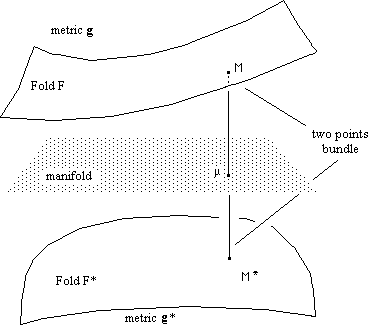
Fig.1 Twin universe : a two-points bundle withe riemanian metric structure ( g , g*).

...We get a point-to-point mapping, linking two "conjugated points" M and M*, which can be described by a same system of coordinates {µ_{i }} . Call F and F* the two folds which compose the bundle. With the two metrics we can build geodesics systems but, as F and F* and disconnected, the two families of geodesics are disconnected. As a conclusion, if these metrics give null-geodesics and if one assume that light travels along them in both folds, any structure of a given fold will be geometrically invisible from the other one.
...In classical General Relativity one considers a single fold, associated to the field equation (Einstein equation) :
(1)

S = c T - L g

where S is a geometrical tensor, c is the Einstein constant, T is the energy-matter tensor and L the so-called, puzzling cosmological constant, introduced by the french mathematician Elie Cartan.
...Consider the following coupled field equations system :
(2)

S = c ( T - T* )

(3)

S* = c ( T* - T )

from which we get immediatly :
(4)

S* = - S

Notice this definitively not imply g* = - g

...The newtonian approximation gives the following Poisson equation :
(5)

D y = 4 p G (r - r*)

. In this new model :

- matter attracts matter, through Newton law.
- twin matter attracts twin matter thrgough Newton law.
- matter and twin matter repel each other through an "anti-Newton law".

What about the classical local check of the RG ?

...The solar system is a very dense portion of the universe. In the adjacent portion of the twin fold, twin matter is psuhed away. Then the system is very close to :
(6)

S = c T

(7)

S* = - T

...The equation (6) identifies to Einstein equation, so that all the classical verifications fit. What about gravitons ? Which path do they follow ? The answer is composed by two arguments :

- Field equations provide macroscopic description of the universe, which ignores the existence of particles and just gives geodesic systems.

- By the way : what's a graviton ?

2 - The question of the repulsive power of vacuum. An alternative answer.

...When we look to equation (2) we see that T* acts like a "cosmological constant". It figures the "repulsive power of the twin universe", which can play a role in non-steady coupled solutions. Assumption of homogeneity and isotropy gives the riemanian metrics the well-known Robertson-Walker form, as follows :
(8)

(9)

...The radial distances between conjugated points (same u, an adimensional "radial distance", with respect to an arbitrary point) are not automatically equal :
(10)

r = R u .......................r* = R*u

Write adimensional coordinates, where t is the time-marker.
(11)

{ t , u , q , j }

... { u , q , j } are classical spherical coordinates. Remember that a field equation is coordinate-invariant. The choice of coordinates remains free, in each fold, where we can define different cosmic times :
(12)

. t ...et ... t*

These variables are linked to the adimensional variable t through :
(13)

t = T t ............t* = T * t

where T and T* are characteristic times scales. Introducing adimensional proper times s and s* :
(14)

we transform the two metrics into their adimensional forms, introducing adimensional scale factors R(t)and R*(t), through :
(15)

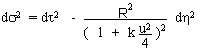
(17)

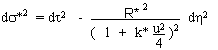
...We put the field equations into their adimensional forms, using :
(18)

Following, these tensors, written in their adimensional forms :
(19)

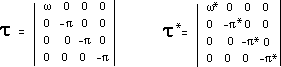
At the end, we get four second order coupled differential equations (instead two, in the classical approach). :
(20)

(21)

(22)

(23)

...We need some additional hypothesis. Assume that the two universes have "parallel lives" during their radiative epoch, i.e :
w (t) = w* (t), which impose negative curvature indixes ( k = k* = -1 ). After decoupling we neglect the pressure terms (dust universes) :
(24-a)

(24-b)

(24-c)

(24-d)

from which we get immediatly :

(25-a)

(25-b)

 
Introducing the mass-conservation in both folds :
(26)

the system becomes :
(27-a)

(27-b)

...Notice that R = R* gives R" = R*" = 0. On another hand, if the two universes were "fully coupled", i.e. R*/R = constant, this peculiar solution would correspond to Friedmann models, with "parallel evolutions". But we consider that they are coupled by gravitational field, through (27-a) and (27-b), which shows that the linear expansion is unstable. If, for an example, if R > R* then R" > 0 and R*" < 0 . The system can be numerically solved. The typical solution corresponds to figure 2.

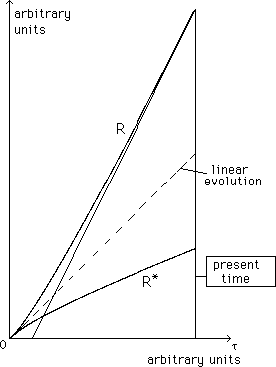
...We see that this system of two universes interacting through gravitational force is unstable. If one universe goes faster, pushed by his twin, the other one slows down. The observed acceleration of our universe is then caused bay the "repulsive powe of its twin universe". The histories of the two differ. Ours is cooler and more rarefied. The twin is warmer and denser.

3 - Other observational confirmations.

...The twin universe theory offers a lot of observational confirmations. See the papers on the website, and references [5] , [6] and [7]. The action of repulsive twin matter on the matter of the galaxies explains the "missing mass effect" and the flatness of the corresponding rotation curve, at distance :

Fig.3 : Galaxy confined by surrounding (geometrically invisible) twin matter.

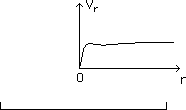
Fig.4 : Corresponding rotation curve.

..