...Ce travail a été présenté par cet auteur lors d'un colloque tenu à l'observatoire de Genêve, en 1989, dont le thème était :

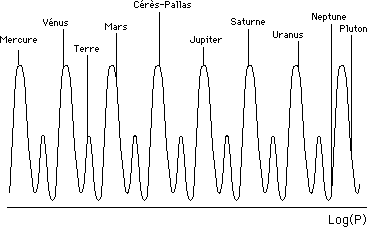
...Le point de départ de Souriau est l'analyse des périodes des orbites des différentes planètes. Il retient alors celle de la Terre : 365 jours et celle de Vénus : 225 jours et calcule, à la fois vers l'aval et vers l'amont la suite de Fibonacci correspondante (ou du type de Fibonacci, où tout terme est la somme de deux qui le précèdent). On sait que dans ces conditions le rapport de deux nombres successifs de cette suite tend vers le nombre d'or.

...Souriau obtient alors ceci :

30                                                Soleil (29 jours)

55                                                Rien

85                                               Mercure (88 jours)

140                                            Rien

225                                            Vénus

365                                            La Terre

590  (1 an et sept mois)             Mars        (1 an et 10 mois)

955                                            Rien

1545 (4 ans et 3 mois)               Cérès-Pallas( ceinture astér)

2500                                         Rien

4045 (11 ans)                           Jupiter ( 11 ans et 10 mois)

6545                                         Rien

10590 (29 ans)                         Saturne ( 29 ans et 5 mois)

17135                                      Rien

27725 (76 ans)                         Uranus (84 ans)

44860                                       Rien

72585 (199 ans)                       Neptune (165 ans),  Pluton (248 ans)

...Coincidence assez étonnante, convenons-en. Souriau étudie ensuite les résonances entre les planètes. Pour ce faire il faut disposer d'un test mesurant si le rapport x de deux périodes, compris entre zéro et 1, est "proche" d'une fraction irréductible :

...Il y a longtemps qu'un tel test a été élaboré par les mathématiciens (Liouville, Hurwitz, Borel, etc). Il s'agit du nombre :

...En désignant par q(x) sa borne inférieure lorsque q décrit l'ensemble des rationnels, q est nul si x est rationnel, petit si x est proche d'un rationnel; il mesure donc l'irrationnalité de x. Les nombres "les plus irrationnels" sont alors le nombre d'or :

et son carré : w² = 1 - w = 0,3820...

 
On peut le constater sur la diagramme donnant la fonction q

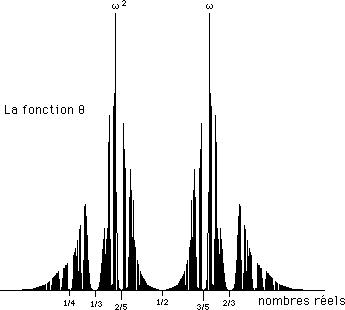
...Cette fonction q (qui n'a rien à voir avec les données
d'observation) est un pur "objet mathématique", une propriété issue de la suite des nombres réels. Cette suite continue sécrète alors ce spectre étrange, peuplé de sortes de lacunes (là où se situe des rapports de nombres entiers, des nombres rationnels, où q = 0).

...Ci-après les périodes de révolution des principales planètes du système solaire, en années :

 
Mercure :             0,2408425

Vénus :                 0,6151866

Terre :                 1,0000000

Mars :                 1,8808155

Cérès-Pallas :      4,604

Jupiter :              11,86178

Saturne :             29,45665

Uranus :             84,0189

Neptune :         164,765

Pluton :             247,68

 
Noter que le rapport entre les périodes de Pluton et de Neptune est :

...Le rapport d'un de ces termes au suivant reste compris entre 1/3 et 2/3. Cinq de ces neuf rapports sont compris entre 0,35 et 0,40. Souriau entreprend alors d'étudier les rapports entre les périodes de différentes planètes. Deux planètes en état de résonance parfaite conduiraient à un rapport de leurs périodes qui serait un nombre rationnel, le quotient de deux nombres entiers.
 

...Souriau décide d'analyser les différentes résonances, dans le système solaire, en l'état actuel. Pour ce faire il prend les rapports des périodes de rotation des principales planètes, deux à deux, et applique le test évoqué plus haut.

 
...Un calcul simple lui permet d'établir la liste des résonances entre grosses planètes (Cérès et Pallas sont les plus grosses des "petites planètes" et leurs périodes ne diffèrent que de 3 jours et se situent dans la ceinture d'astéroïdes), dont le test q est inférieur à 0,1 (dénominateur ? 6). :

 
Neptune-Pluton : x = 2/3 x 0,9980 q = 0,01

Uranus-Neptune : x = 1/2 x 1,0199 q = 0,04

Uranus Pluton : x = 1/3 x 1,0176 q = 0,05

Vénus-Mars : x = 1/3 x 0,9812 q = 0,06

Jupiter-Saturne : x = 2/5 x 1,0067 q = 0,07

 
...Cette table montre que les deux planètes les plus éloignées, Neptune et Pluton, présentent des résonances particulièrement marquées. Elles forment donc un couple "à part" vis à vis des autres et Souriau décide de les négliger dans l'analyse qui va suivre, en opérant une analyse de Fourier des périodes :

...Pj étant les périodes des planètes, de Mercure à Uranus. Les rapports successifs des périodes sont compris entre 1/3 et 2/3. La figure suivante évoque l'allure de la courbe IF(a)I pour a variant entre 1/3 et 2/3. Pour plus de lisibilité Souriau a porté sur le graphique IF(a)I⁴.

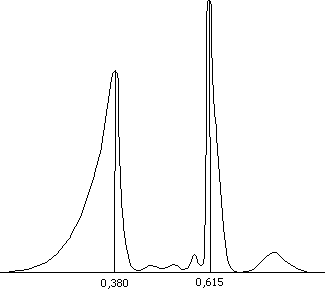
...Deux pics significatifs apparaissent pour les valeurs 0,615 et 0,380 en coincidence précise avec les pics de la figure 1 (w = 0,618 et w² = 0,380). Souriau superpose alors ce spectre avec la fonction q  :

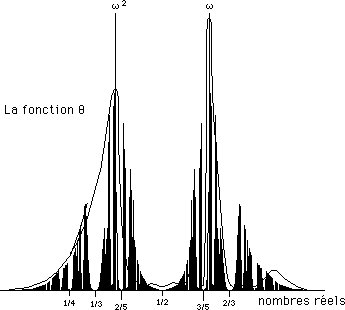
et il conclut à un effet global de non-résonance, à l'exception du couple résonant Neptune-Pluton. Le déphasage de F entre les deux pics peut s'interpréter par la transformée de Fourier réciproque : à partir d'un certain nombre de raies ak sélectionnées dans le spectre F on construit la fonction F :

...Les valeurs de Pj sont alors proches de certains maxima de la partie réelle de F. Souriau limite alors ce spectre aux deux raies a1 = w et  a2 = w² et obtient la courbe de la figure ci-après, où sont par ailleurs portées les périodes réelles des planètes.