...We include antichron elements in the dynamic group. Then we get movements and moments involving T-symmetry, like PT-symmetric movements and CPT-symmetric movements. The first evoke the Feynmann's vision of antimatter and the second the so calle "CPT theorem". But tim-inversion, from coadjoint action, changes the sign of the mass and energy. The PT-symmetrical of a particle of matter does not longer identify to Dirac's antiparticle, as Feynmann thaught. It is an antiparticle, but with negative mass. Same thing for CPT theorem : the CPT-symmetrcal of a particle of a particle of matter is a partcle of matter, but with negative mass.

1) Introduction.

...In former papers ( [1] and [2] ) we have given a geometrical interpretation of antimatter. Matter and antimatter are suppose to have their personal playing field {z i > 0} and {z i < 0} in a ten dimensional space :

(1)

composed by space-time { x , y z , t } plus six additional dimensions. The playing field of photons corresponds to the {z i > 0} plane.

...Our 16 dimension groups gives six additional scalars, identified to quantum charges. The basic geometric definition of anti matter we suggest corresponds to :

(2)

...Through a four component group [2] we have shown that, in such conditions, the z-symmetry goes with a C-symmetry, which corresponds to Dirac's antimatter [3], [4] and [5].

Feynmann suggested an alternative description of anti matter. The argument is the following.

If we consider the evolution of a particule owing a mass m and an impulsion p, its energy is :

(3)

Suppose that this particle, moving in the "twin fold" F*, goes from a state 1 ( P*1 ) to a state 2 ( P*2 ).

We just keep one space marker x = x¹ ( doing x² = 0 and x³ = 0 ). The amplitude of such an evolution is :

(4)

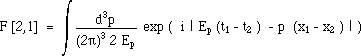
( where, conventionnaly, c = h = 1 ) .

 
...This path owns a conjugated image in our space-time fold F. Due to the effect of PT symmetry, the "vision" of some hypothetic observers, located in the folds F and F*, would be different. For the observer located in the fold F the particle, owing a mass m and an impulsion p moves from the state 2 to the state 1 ( P and T both add a minus sign to the impulsion ). This movement occurs during a time-interval Dt' = t'¹ - t'² = t² - t¹, and from a position x₂ to a position x₁.

...If, for an example, a neutrino ne , with a left helicity, moves in the fold F*, from the "point of view" of the fold F its helicity will be reversed : it will be an antineutrino.
 

3) Shifting to complete extended Poincaré group.

...The idea of Feynmann ( PT-symmetrical particles ) implies the presence of antichron components in the group. In the group presented in reference [1] and [2] space inversion is already present, due to their presence in the basic orthochron Lorentz group. They are required to take account of disntinct helicities for photons and neutrinos.

We could extend the group, introducting a time-switch matrix :

(5)

...Multiplying and the elements of the orthochron sub-group we could build the antichron components. But let us do it in a simpler way :

(6)

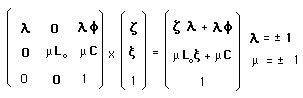
...This group contains all the required components : orthochron and antichron, but such writing evidences the PT-symmetry ( m = - 1 ) in a convenient way.

...This is a eight components group ( 2 x 2 x 2 ). The groupe of [2] is a sub-group of (6) whence the group of [2] was a sub-group of the one of [1].

The coadjoint action is found to be :

(7)

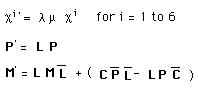
Here again, we identify the scalars c i to the particle's charges set :

(8)

l = - 1 achieves :

(9)

Here again z - Symmetry is assimilated to matter-antimatter duality.

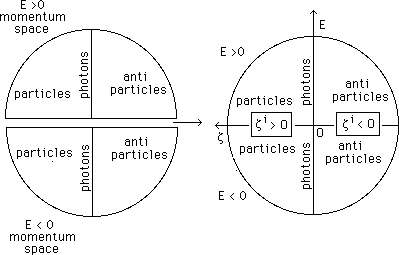
...With this material we can analyze the impact of the different components on the momentum. As we have antichron terms our momentum space must be extended to ( E < 0 ) momentums sectors. See figure 1.