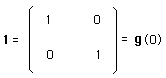|
1 |
...Tout ce qui va suivre dans ce domaine va tourner autour des groupes. Peut-on donner un aperçu vulgarisé de cette partie, sans produire un cours complet sur les groupes. Par ailleurs, quelle relation entre groupe et particules? Tout cela semble bien mystérieux pour un néophyte.
...D'abord qu'est-ce qu'un groupe ? Dans ce qui suivra, une simple famille de matrices carrées de format (n,n). L'opération permettant de les faire agir les unes sur les autres est la multiplication matricielle (ligne-colonne).
Toutes ces familles de matrices posséderont toujours un élément neutre, du type :
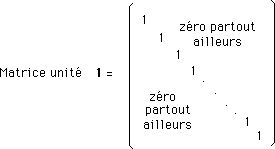
...Un groupe obéit évidemment à des axiomes, ceux de Sophus Lie. Les axiomes des groupes sont plus généraux que ceux des axiomes de matrices mais, pour nous, n'existeront que les groupes de matrice carrées, associées à une opération de composition qui soit la classique multiplication ligne-colonne, notée x .
1 - Premier axiome des groupes. Il existe une opération de composition , permettant de composer deux éléments d'un ensemble , et cette loi de composition, par rapport à cet ensemble-là, est interne , c'est à dire, dans le cas de la multiplication matricielle :
Soit g1 et g2 des éléments d'un ensemble de matrices carrées G. En les composant on obtient une matrices carrées :
Il est alors indispensable que la matrice appartienne à l'ensemble
G, qu'elle soit de même type, c'est à dire que :
![]()
...Vous
me direz : "les matrices carrées de format (2,2) : deux lignes, deux
colonnes, ou (5,5) : cinq lignes, cinq colonnes, satisfont ce critère,
puisque g3 = g1 x
g2 est une matrice de même format.
Mais cet ensemble est .... trop vaste, trop flou. Vous ne pourrez rien en
faire, et en tout cas pas de la physique. Et puis il ne satisfait pas a
priori les axiomes suivants. Voir plus loin
Donnons un exemple simple d'un ensemble de matrices, à un paramètre a , qui forme un groupe :
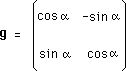
Composons deux matrices de ce type :
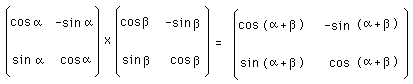
ou :
La matrice produit peut s'écrire :
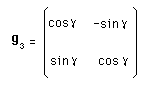
Elle est bien du même type que g1 et g2 . C'est à dire que :
![]()
Contre-exemple. Considérons une autre famille de matrices à un paramètre a
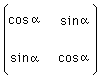
Composons deux matrices de ce type :
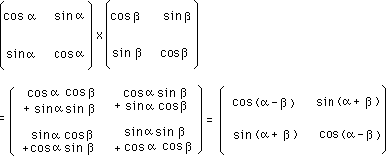
La matrice obtenue n'est pas du type (5). Comme dirait Magritte "ceci n'est pas un groupe". Il a suffi de changer un signe.
2 - Second axiome des groupes :
On doit avoir un élément neutre, noté e tel que :
g "composé" e = e "composé" g = g
...Dans les matrices carrées cet élément neutre est toujours la matrice unité, notée 1 , avec un caractère gras : on notera désormais toutes nos matrices et en règle générale tout ce qui n'est pas un scalaire par un caractère gras, réservant les caractères maigres pour les scalaires. Ceci s'écrirait, dans ces condition :
g x 1 = 1 x g = g
Dans notre exemple :
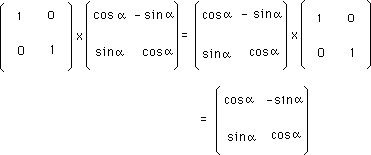
On remarquera au passage que :