Gauge cosmological model with variable light velocity. Comparizon with QSO observational data.
Jean-Pierre
Petit
and Maurice Viton
(Laboratoire d'Astronomie Spatiale. Traverse du Siphon.13012. Marseille)
Modern Physics Letters A Vol.4 , n°23 (1989) pp. 2201-2210
ABSTRACT :
...After a complement to previous papers on the gauge invariance of the Boltzmann collisional operator, we compare a recent homogeneous set of data on radio-QSOs, including angular sizes and bending of lobes, with what is expected from either our new cosmological gauge model or the most commonly accepted Friedman model with qo = 1/2 . It is shown that the new gauge model provides a much better fit to the angular size distribution vs. redshift and similarly to the bending, thanks to crude hypothesis on the mechanisms involved with the formation of jets.
1) INTRODUCTION
...In references [1] and [2] , hereafter paper I and paper II respectively, we have previously developped a cosmological model in which all the so called constants of physics were made free, so that we had to introduce new physical laws, gauge laws, in order to link conveniently these constants :
c (velocity of light), G (gravitation), h (Planck's constant), me (electron mass), mp, mn (proton and neutron mass ). It was shown at first that the general relativity theory does not require the absolute constancy of G and c, but only the absolute constancy of the ratio G/c2 (Einstein's constant of the field equation). This brought the first linking relation. The other came from geometric considerations : we assumed that the characteristic lengths like Jeans length, Schwarzschild length and Compton length followed the variation of the scale parameter R(t).
Combining these new physical
laws we got the following relations :
(1)
![]()
(2)
mp = mn ( nucleon's mass ) » R
(3)
h » R3/2
(4)
G » 1/R
(5)
V ( velocity ) » R-1/2
(6)
r » 1/R2
In addition we found a
single cosmic model, with negative curvature, indifferently filled by photons
or matter or a mixture of the two, with non zero pressure, and obeying the single
law :
(7a)
![]()
...In the paper II we refound the Hubble's law, due to the secular variation of the Planck constant (which was found to vary like t) and not to the expansion process. In this constant energy model, geometrical considerations made some characteristic energies like the ionization energy to vary like R(t), and it was found to be consistent with additional gauge relations applying to electromagnetism. Then it appeared possible to derive the distances of light sources from the red shift data. They were found to be quite close, for moderate z values, to the classical values derived from a Friedman model with qo = 1/2 , since the ratio :
(7b)
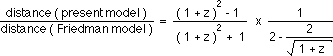
remains close to unity within 5 percent for z £ 2 .
2) A SHORT COMPLEMENT ABOUT THE GAUGE INVARIANCE
...In the paper I, section 5, we had shown that some fundamental equations (Vlasov, Schrödinger, Maxwell) were invariant under the suggested gauge relations. Let us show that the Boltzmann collision operator is invariant to.
Writing this equation.
(8)
![]()
...f
is the velocity distribution function, g is the relative velocity of two particles
in an encounter, b is a length (impact parameter), e an
angle. Introduce adimensional variables, through :
(9)
t = t* t ; f = f* x ; V = V* w ; g = V* g ; r = R* z
Y = (G*m*/R*) j ; b = R* b
The characteristic velocity
distribution function is :
(10)
![]()
...Following
the gauge relations as defined in paper I , G*m*/R* varies like 1/R*. V* varies
like 1/R*1/2. m* varies like R* (m*V*2
is constant). The energy k T is constant. To sum up f * » R*-3/2,
and hence :
(11)
![]()
...Such
a dimensional analysis gives terms varying respectively like 1/t*,
V*/R* = 1/R*3/2 , 1/R*3/2 , which implies again :
(12)
R* » t* 2/3
and hence the invariance of the Boltzmann operator.
3) OBSERVATIONAL TESTS.
...After this short parenthesis, let us turn to a comparison of various models with the radio data on 134 QSOs recently published by Barthel and Miley [ 3, hereafter BM] , in which they show that distant DSOs have smaller angular sizes, larger bendings and higher luminosities than those nearby. Note however that we do not intend to discuss the given intrinsic powers here, since the physical mechanisms involved in the generation of relativistic jets are not yet clearly understood.
...The situation is appearently simpler concerning the angular size and bending of radiosources, since geometric properties are mainly concerned a priori in both cases, though we cannot ignore that important systematic effects might be at work and we adress the reader to the related comprehensive discussion of BM on the detailed mechanisms involved. In short :
- interaction with the intergalactic medium (IGM) can disrupt very efficiently the initially collimated jets, resulting into the formation of large, turbulent lobes (4) of lesser extension : if it is clear that such effects can modify significantly the angular size distribution at a given redshift, more complicated mechanisms have been invoked by BM to explain the stronger bending of lobes observed at large redshifts.
- possible evolutionary effects in all the elementary mechanisms implicated above, including gauge processes not yet identified.
- observational bias such as the well-known Malmquist's, introducing an underestimate of angular sizes for distant QSOs.
...Now, let us suppose in this paper that such potential effects are not dominant in the data, i.e. that the distribution of angular size and bending vs. redshifts may be considered as good tests for discriminating between different cosmological models and show that the new gauge model provides better fits to these distributions than do the conventional models.
3a The angular size.
...The angular size of extragalactic objects has often be considered as a powerfull test for cosmological models. So, let the subscript 1 refer to the emission epoch and subscript 2 to the reception epoch : since the light emited by the edges of a source at time t1 follows radial pathes, the angular size f is conserved for a present observer, so that we can write classically, whatever the model :
(13)
![]()
where D(t1) is the linear diameter of the source and d(t1) its metric distance.
In the classical Friedman model with qO = 1/2 ( the so called Einstein-de-Sitter's )
D(t1) = D constant
R (t1) = R (t2) / ( 1 + z )
and d(t1) = R (t1) u where :
(14)
![]()
and hence some kind of a paradox arises since the angular size obeys :
(15)
![]()
This function has a minimum for z = 1.25 , and then it tends to grow linearly with z .
Now, with the new gauge model we have
D(t1) = D(t2)/(1+z) ,
R(t1)
= R(t2)
/ ( 1 + z )
and d(t1)
= R (t1)
u also
but with :
(16)
![]()
and the angular size obeys :
(17)
![]()
When z tends to infinity, f tends to a constant, a readily different behaviour and in qualitative agreement with the data.
(18)
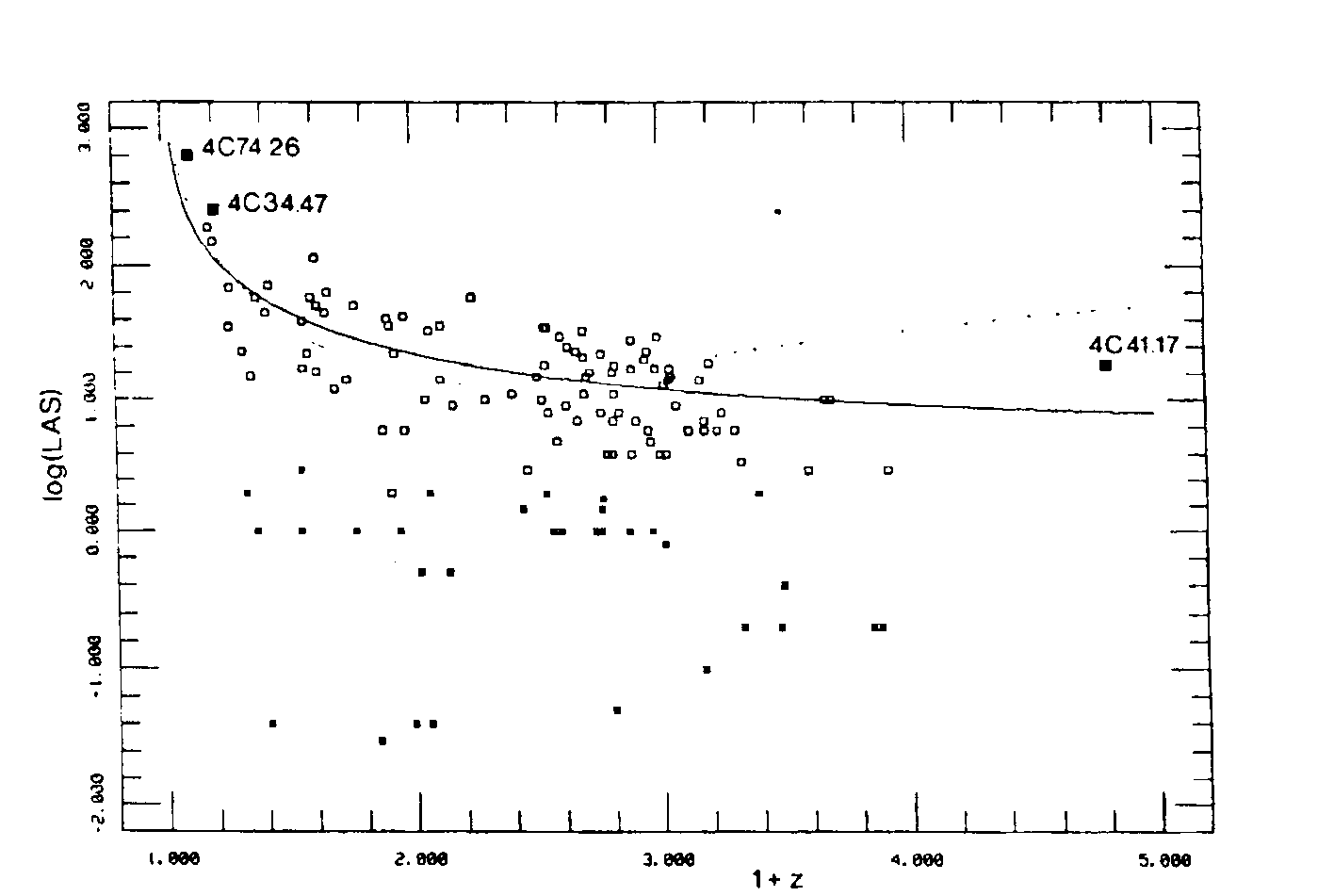
Fig 18 : The largest angular size (LAS, in arcsecond), on a logarithmic scale versus redshift for the 95 extended sources with "T", "D1" and "D2" morphologies (squares) and the 33 compact sources with "SSC" morphologiy (asterisks). The two curves represent the fits of the gauge model (continuous line) and the Einstein-De Sitter model (dotted line) derived for extended sources in this paper. Three additional radio-sources of very large extent are shown for comparison. 4C41.17 being the farthest galaxy presently known, 4C74.26 the largest radio-source associated with a quasar.
...In order to compare quantitatively how both models fit the data, let us write f = fof(z) where f(z) is a characteristic function as predicted above by each model. Linear regressions have been performed between f(z) and the "largest angular size" [ LAS after BM ) data, either for their complete sample of 134 QSOs, or for a reduced sample of 83 QSOs in which only two-sided lobes sources were selected, i.e. those with the "T" or "D1" morphologies defined by BM, thus excluding the steep spectrum core or "SSC" and the one-sided lobe or "D2" sources, so as to test for possibly different properties of compact and extended sources. The results of the regressions were as follows, all the given linear coefficients and their rms errors bars being in arc second units :
- with the Einstein-de-Sitter model :
F = ( 28.8 ± 2.9 ) f(z) - ( 89.3 ± 20.1 )
for the complete sample, and
F = ( 31.3 ± 3.3 ) f(z) - ( 90.5 ± 20.8 )
For the reduced sample.
- with the gauge model :
F = ( 21.5 ± 2.11 ) f(z) - ( 19.1 ± 19.6 )
for the complete sample, and :
F = ( 24.3 ± 2.3 ) f(z) - ( 17.3 ± 19.8 )
for the reduced sample.
...It is clear that the new gauge model provides a fairly better fit to the data since whatever the sample, the moderate constant term it implies is marginally significant from a statistical point of view and hence the (expected) zero value is highly probable. The situation is quite opposite with the conventional model, here also whatever the sample, since the constant term is highly significant from a statistical point of view and its large, negative value is unacceptable on theoretical grounds, unless one supposes that very strong systematic effects as those suspected above are at work in the data.
3b. The bending.
...Let
us show also that the more bent, distorted appearence of distant QSOs pointed
out by BM may be curiously explained by the new gauge model, providing here
again that is not an artefact resulting from various systematic effects. Since
in the new model it is assumed that all the energies are conserved during the
cosmic gauge process, we can include the conservation of the rotational energy
of the QSO core emitting the jets :
(19)
![]()
As m » R , I » R3 and W» R-3/2 W » 1/t » ( 1 + z )3/2, in curious agreement with the one-dimensional lower law fit performed by BM on the reduced sample ( since the bending is only defined in this latter case ), that is :
(20)
![]()
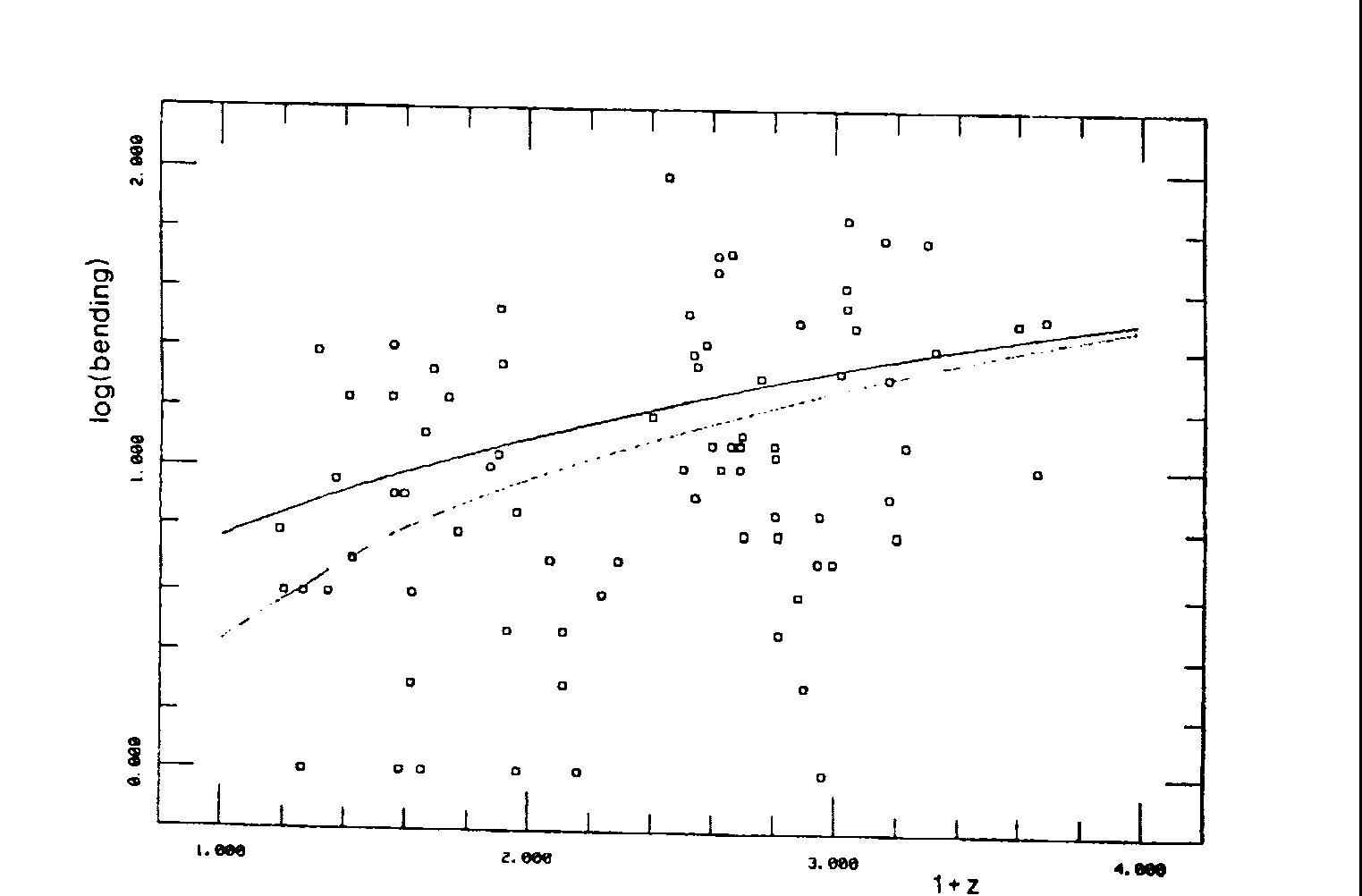
Fig 21: The bending (in degree) on a logarithmic scale versus redshift for the 83 extended sources with "T" and "D1" morphologies only, for which it is defined. The continuous curve corresponds to the fit of the gauge model, indicating that angular speeds where higter in the past, while the dotted line represents the power law fit of Barthel and Miley (BM)
...Now let us suggest a crude explanation, refering to the recent analysis of Greyber [5) on the nature of the central engines in QSOs responsible for their tremendous energy production rates : if we accept the figure (i) that the plasma blobs are ejected at high velocities from the central engine, continuously or not, along the magnetic dipole axis of the QSOs and (ii) that this latter is not generally coincident with their angular momentum axis, then we are faced with a model similar to a rotating "garden sprinkler", in which the jets will bend into some kind of a spiral of Archimedes, as long as the interaction with the IGM remains neglectible. And even if this interaction becomes significant at some distance from the nucleus, the jets will stop to expand there, resulting into an increased bending. Since there is no reason why the IGM density would be spherically distributed around QSOs, such interactions could account for the frequently assymetries in their jets together with random effects on the overall bending, as it has been discussed by BM.
...As a consequence, the higher the redshift of the QSO, the higher its angular velocity because of the cosmic gauge process and hence the larger the bending of its jets.
4) CONCLUSION.
...We have focussed on specific features recently evidenced in the distribution of angular sizes and bending vs. redshift for an homogeneous set of 134 radio-QSOs. We found interestingly that our gauge model with "variable constants" provides better fits to these distributions than the conventional Einstein-de-Sitter model, providing (i) that the observed trends (smaller angular size and larger bending of distant QSOs) will be confirmed by future observations, (ii) that these trends are not dominated by various effects or artefacts, and (iii) that the crude assumptions wa made on some of the mechanisms involved are real. Also, further investigations on the intrinsic power of these sources are needed to understand if the gauge model provides a better understanding of the observed trends, i.e. that the luminosity of distant QSOs is much greater than for those nearby.
5) REFERENCES.
[ 1] J.P.PETIT : Interpretation of cosmological model with variable light velocity. Modern Physics Letters A, Vol.3 n° 16 November 1988
[ 2] J.P.PETIT : Cosmological model with variable light velocity. The interpretation of red shifts. Modern Physics Letters A, Vol.3 , n° 18, December 1988.
[ 3] P.D.BARTHEL & G.KMILEY. Evolution of radio structure in quasars : a new probe of protogalaxies? - Nature Vol 333, 26 may 1988.
[ 4] M.L.NORMAN, J.O. BURNS and M.E. SULKANEN : Disruption of the galactic radio jets by the shocks in the ambient medium, Nature 335 (1988) 146.
[ 5] H.D.GREYBER : The importance of strong magnetic fields in the Universe, Comments Astrophys. 13 ( 1989 ) 201.
