AN INTERPRETATION OF COSMOLOGICAL MODEL
WITH VARIABLE LIGHT VELOCITY.
Jean-Pierre PETIT.
Observatoire de Marseille
For scientific correspondance : Chemin de la Montagnère, 84120,
Pertuis. France.
Modern Physics Letters A, Vol. 3, n°16, nov 1988, p.1527
ABSTRACT : A cosmological model with variable c, h, G is proposed. The characteristic lengths of physics ( Compton, Jeans, Schwarzschild ) are assumed to vary like R(t). Both light and matter's worlds are found to obey the same law R » t2/3 The Planck constant is found to vary like t and the gravitation one like 1/R, while the Planck length vary like R. The particle masses follow m ~ R. The Hubble law still apply. The redshifts come from the secular variation of the Planck constant
1 - INTRODUCTION
...Since 193O the constancy of several so called constants of physics have been criticized by many authors [1,2,3,4] . Accurate laboratory measurements show that these values appear quite constant in our to-day's space time field, which is very small with respect to the whole space time, although Van Flandern [6] claimed for observational evidence of the variation of the gravity constant G. As far as we can see the extension of the constancy of the light velocity, and others so called "fundamental constants" over the overall cosmic scale is a still debatable hypothesis. The purpose of this paper is to examine some of the consequences of a model in which the 'constants" (especially the light velocity) are assumed to vary with time.
2) THE POSSIBLE SECULAR VARIATION OF c
...Milne [1] tried the first to propose an attempt of this type. He suggested that the observed red shifts are due to some secular change of the Planck constant and not to the classical Doppler effect. If the energy of the traveling photon remains constant, the apparent decrease of the observed frequency would be only due to the linear increase of h with the cosmic time t. In addition Milne [1] suggested a decrease in time of the gravity constant G.
...Similarly Fred Hoyle [2] argued against the assumption of the constancy of the mass content of the universe. He also suggested a secular change of G and constant creation of matter. Dirac [3,4] , starting from an hypothesis about the variation in time of some large numbers, built with characteristic physical quantities ( like the ratio of the electromagnetic force to the gravitational force ), got a variable G and a constant creation of matter. Later Canuto and Hisieh [8] , Lodenquai [5] and Julg [7] explored some consequences of Dirac's initial idea. But, surprizingly, no one contested the absolute constancy of c.
In the
field equation the so called Einstein constant
c
is determined by identification to the Poisson equation, which gives :
(1)
![]()
...The quantity c must be an absolute constant with respect to the four dimensions, for the field equation to be divergenceless. But once the identification mentioned above refers to a steady situation it does not imply the absolute constancy of G and c. A world model could a priori be built, with variable G and c, with respect to the cosmic time ( which will be defined later ), if the ratio G/c2 remains an absolute constant.
In the sequel of the paper we are going to analyze the effects of a secular variation of the light velocity.
3. SUGGESTING GAUGE RELATIONS
The Robertson-Walker
metric, based on the isotropy and homogeneity assumptions, leads to the following
system :
(2)
![]()
(3)
![]()
...In this system, k is the sign of the curvature, p the pressure and r the density of energy-matter. In the classical model we define the cosmic time t from the chronological variable x°, by x° = c t , where c is considered as an absolute constant. In addition the wavelength of the photon varies like R.
Let us
consider the less restrictive following condition :
(4)
d x° = c(t) dt
which represents
an alternative interpretation of the chronological parameter x° . We are now
going to relate the main physical constants to R, considered as a gauge parameter
:
(5 )
![]()
(6)
m ( particle's mass ) » R
(7)
h » R3/2
(8)
G » 1/R
...Referring
to the relation (1) notice that G/c2 = constant. In addition if V
is the relative velocity of a given element , for example the random velocity
of a galaxy in a cluster, or the velocity of a free particle in a cloud, we
assume that V follows the secular variation :
(9)
V » R-1/2
If we suppose
that the number of particles is conserved, the matter density
r
obeys :
(10)
r » 1/R2
...As a consequence we can express the cosmic evolution through a gauge process, i.e. the Compton wavelength, the De Broglie wavelength, the Schwarzschild length and the Jeans length are found to vary like R.
In addition
our model still considers mc2 = constant and :
(11)
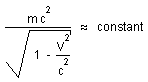
...The classical model saved the masses, as assumed to be constant, but not the total matter-energy, through the variation of the the cosmic background energy. In our scenario it is just the reverse : the energy-matter is constant in time, not the masses. In addition, one should notice that the quantity Gm2/R, which can be considered as a characteristic gravitational energy, is conserved.
...Since the energies are conserved in our model, the moment as defined as mVi varies like R1/2. It is only constant if we define them as ruic.
Finally the Planck length varies with time like R(t), the Planck time varies like t and the gravitational forces like 1/R(t).
4. THE EVOLUTION EQUATION
Introducing
(4) into the system (2),(3) we obtain the following equations :
(12)
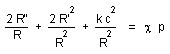
(13)
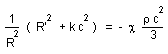
The use
of the following equation of state
(14)
![]()
leads to
:
(15)
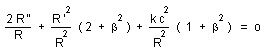
...In
the case where R = a tm the parameter
b disappears
from (15). From (5) Rc2 = Roco2
is an absolute constant, Ro and co being the present values of the gauge parameter
R and light velocity c. The only possible value for k is -1, which means that
in our model the curvature is negative. Then the evolution law becomes :
(16)
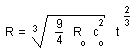
Here, at
contrary to the classical models, light and matter the same evolution law. Moreover
:
(17)
![]()
...If
we know to, the age of the universe, and co , the present value for the
light velocity , we could derive the present value of the gauge parameter of
the universe Ro =
(3/2) co to, with the use of :
(18)
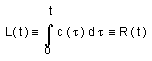
The consequence is that the horizon is found to be identical, at any time, to the gauge factor R(t).
5. GAUGE INVARIANCE OF SOME FUNDAMENTAL EQUATIONS
...Let
us take first the Vlasov equation, referring to collision free fluids. f (r,V,t)
is the velocity distribution function, which depends on the position vector
r, the velocity vector V and the time t. Y
is the gravitational, so that - m ¶
Y/¶
r is the force acting
on the particle whose mass is m.
(19)
![]()
Introduce non-dimensional variables, such that :
t = t* t ; f = f* x ; V = V* w ; r = R* z ; Y = ( G*m*/R*) j
The equation
(19) becomes :
(20)
![]()
...Introduce
the precedent gauge relations G* »
1/R* , m* »
R*.
The dimensional analysis of the equation (2O) gives V*
»
1/(R*)1/2 and
:
(21)
R* » t*2/3
These relations
can be interpreted as gauge relations and related to the solution (16). Consider
now the Schrödinger equation :
(22)
![]()
Introduce :
t = t* t , r = R* z , h = h* h , m = m* m , U = U* u.
The dimensional analysis of the equation (22) gives :
(23)
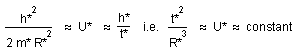
i.e. R*
»
t*2/3 . Now let us write the Maxwell equations, referring to en empty space
:
(24)
![]()
(25)
![]()
and write :
E = E* e , B = B* b, r = R* z , t = t*t, c = c* w
We get
:
(26)
![]()
(27)
![]()
Combining with c* » 1/R*1/2 we refind R* » t2/3 .
6. CONCLUSION .
...In this paper we have derived some of the implications of letting the fundamental constants varying with time. This can only be done with the addition of some further gauge constrainsts. Following the Milne's suggestion [ 1] the classical interpretation of the red shift in terms of Doppler effect has to be replaced by another one taking account the secular change of the Planck constant. The fundamental parameters R and c are related to each other by some gauge relation. The particle masses vary like R while the energy-matter and the gravitation energy are conserved.
...This model predicts that the cosmological horizon L(t) should be identical to R(t), which would justify the overall homogeneity of universe. The curvature of space should be negative and the gauge relationship between R and t should be R ~ t2/3.
...The Planck's constant would vary like t, and the gravitational constant G like 1/R, such as the Planck's length would vary like R, as well as the Planck's time would vary like t. The gravitational force would vary like 1/R.
REFERENCES :
[ 1] E.A. MILNE : Kinematic Relativity Oxford 1948.
[ 2] F.HOYLE & J.V.NARLIKAR : Cosmological models in conformally invariant gravitational theory. Mon. Notices Roy. Astr. Soc. 1972 155 pp 3O5-325.
[ 3] P.A. DIRAC : 1937, Nature, 139,323
[ 4] P.A. DIRAC : 1973 Proc. Roy. Soc. London , A333, 4O3
[ 5] V.CANUTO & J.LODENQUAI : Dirac cosmology, Ap.J. 211 : 342-356 1977 January 15.
[ 6] T.C.VAN FLANDERN : Is the gravitational constant changing ? Ap.J, 248 : 813-816
[ 7] A.JULG. Dirac's large numbers hypothesis and continuous creation. Ap.J. 271 : 9-1O 1983 August 1
[ 8] V.CANUTO & S.H. HSIEH : The 3 K blackbody radiation, Dirac's large numbers hypothesis, and scale-covariant cosmology. Ap.J., 224 : 3O2-307, 1978 September 1
[ 9] ADLER R. BAZIN M. SCHIFFER M. : Introduction to general relativity. Mc Graw Hill 1965.
[ 1O] SOURIAU J.M. : Géométrie et relativité. Hermann ed, France, 1964
