J.P.Petit : "Univers énantiomorphes à flèches du temps opposés", CRAS du 8 mai 1977, t.285 pp. 1217-1221
J.P.Petit : "Univers en interaction avec leur image dans le miroir du temps". CRAS du 6 juin 1977, t. 284, série A, pp. 1413-1416
...Dans le papier qui va suivre nous avions tenté
de négocier le lien point par point (application involutive) entre
les points du voisinage de la Terre (à échelle cosmologique)
et les points conjugués du second univers (qu'on appelle celui-ci univers
jumeau : twin universe, ou univers-ombre : shadow universe, ou univers-fantôme
: ghost universe, appellation dans notre esprit équivalente), en utilisant
une relation d'antipodalité , qui impliquait une hypothèse
de départ concernant la topologie de l'objet géométrique.
Par la suite nous nous sommes aperçus que cela n'était pas nécessaire
puisqu'on pouvait définir la structure locale (F,F*) en tant que revêtement
à deux feuillets d'une "variété squelette". La structure
est alors celle du revêtement à deux feuillets d'un projectif
P3, équivalent à trois dimensions du projectif P2, à
deux dimensions, plus connu, donc la représentation la plus connue
est la surface trouvée en 1902 par l'autrichien Werner Boy, voir la
figure 184 (en principe une animation, quand le site sera complet).
...Boy était un élève du grand mathématicien Hilberth, lequel se déclara fort satisfait de l'invention de son élève. Pour la petite histoire, après son invention, Boy quitta l'université et on n'entendit plus jamais parler de lui. Toutes les recherches effectuées par les historiens pour retrouver sa trace furent vaines. On ne sait pas s'il mourut d'une mauvaise grippe ou s'il finit ses jours comme plombier.
...Les géomètres savent qu'on peut mettre en coincidence tous les points d'une sphère S2 selon un projectif P2, comme évoqué sur La figure 10 de l'article ci-après. Le pôle nord est ainsi amené en coincidence avec le pôle sud et l'équateur s'enroule sur lui-même selon le pseudo-équateur de la surface de Boy, également indiqué. Ce revêtement à deux feuillets est indiqué sur la figure 11 de l'article. On notera, du moins en deux dimensions, que cette opération met en coincidence des objets énantiomorphes, en miroir. Les figures 12 et 13 sont des images didactiques qui montrent alors comment les grumeaux viendraient se placer dans les lacunes de la région antipodale.
...Ce système du revêtement à deux feuillets peut être étendu à trois et même quatre dimensions, avec des sphères S3 et S4, revêtant respectivement des projectifs P3 et P4.
Avant d'aller plus on peut familiariser le lecteur avec la géométrie de cette étrange surface de Boy. Celui-ci pourra également trouver différentes déclinaisons de l'objet dans le Topologicon (Ed. Belin, 1984).
...Ce qui peut surprendre évidemment le lecteur c'est le fait que cette surface se recoupe elle-mêle selon un ensemble d'auto-intersection qui est une courbe trifoliée, évoquant un hélice de navire :

...Sur ce dessin, à gauche, on a ménagé une ouverture de manière à montrer le point triple, où se croisent trois nappes. Cette surface semble bien particulière. En fait cet objet est un excellent exemple qui permette d'illustrer le concept d'espace de représentation (3d) évoqué plus haut.
...Le point triple T et la courbe d'auto-intersection ne sont dûs qu'au mode de représentation du projectif P2 dans R3. Une sphère, un tore, peuvent être plongés dans R3, c'est à dire se prêter à des représentation, topologiquement équivalentes, où la surface ne se recoupe pas elle-même. Mais il est impossible de plonger le projectif P2 dans R3. On ne peut que l'immerger . Le dessin ci-dessus (la surface de Boy) est donc une immersion du projectif dans R3. Une immersion d'une objet 2d est un mode de représentation dans R3 où on trouvera une ligne de points doubles (la courbe d'auto-intersection), le long de laquelle on trouve deux plans tangents, plus un certain nombre de points triples où trois nappes se coupent. La surface de Boy n'est qu'une parmi l'infinités de façons d'immerger le projectif P2 dans R3. On en trouvera d'autres dans un article, qui sera inclus dans le site, intitulé "les différentes visages du plan projectif".
...Il est assez facile d'obtenir des images de la surface de Boy, à travers une représentation paramétrique que nous avons inventée et publiée
---> Le lecteur trouvera
dans le sous-site MATHEMATIQUES, entre autre, la reproduction de la note aux
comptes-rends publiées en 1981 à l'Académie des Sciences
de Paris, avec J.Souriau ( non, ça n'est pas le célèbre
mathématicien, mais un de ses fils, Jérôme, devenu par
la suite informaticien), dont la référence est :
"La représentation analytique de la surface de Boy", Note aux Comptes
Rendus de l'Académie des Sciences de Paris, tome 293 (5octobre 1981)
série 1 pp. 269-272
On y montre que la
surface possède alors de méridiens elliptiques. Cette propriété
permet de la tracer aisément. Ci-après, le programme figurant
dans la page de garde de ma bande dessinée le Topologicon.
Programme BASIC
10 CLS
50 PI = 3.14159 : P3 = PI/3 : P6 = PI/8 : P8 = PI/8
90 FOR MU = 0 TO PI STEP .1
95 P = P + 1
100 D = 34 + 4.794 * SIN (6*MU -P3)
110 E = 6.732*SIN(3*MU-P6)
120 A = D + E : B = D - E
130 SA = SIN (P8*SIN(3*MU))
140 C2 = SQR ( A * A + B * B) : C3 = ( 4 * D * E) / C2
160 CM = COS (MU) : SM = SIN (MU)
180 FOR TE = 0 TO 6.288 STEP .06
190 TC = A * COS (TE) : TS = B * SIN (TE)
200 X1 = C3 + TC - TS
210 Z1 = C2 + TC + TS
250 REM VOICI LES 3 COORDONNEES
300 X = X1 * CM - Z1 * SA * SM
310 Y =Y1 * SM + Z1 * SA * CM
350 REM INTRUCTION POUR AFFICHER LES POINTS
360 PSET (X,Y),1
400 NEXT TE : NEXT
MU
...Pour mémoire c'est cette découverte de la possibilité de représenter cette surface à l'aide de méridiens elliptiques qui permit ultérieurement au mathématicien Apéry d'obtenir la première représentation sous forme implicite, du sixième degré :
que nous ne reproduirons pas (elle est d'ailleurs assez compliquée et nous sommes convaincus qu'il doit en exister de plus simples, mais ceci fera l'objet d'un autre document qui sera inclus dans le site MATHÉMATIQUES).
...La bouteille de Klein est plus connue des lecteurs. Il est également impossible de la plonger dans R3. Elle se présente alors, sous sa forme la plus classique, sous la forme d'une immersion dotée d'un ensemble d'intersection qui est une simple courbe fermée.
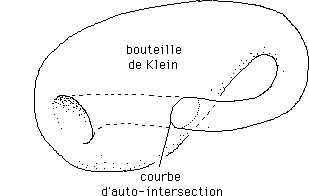
...Le revêtement à deux feuillets de la surface de Klein est un tore T2, de même que celui de surface de Boy (projectif P2) est une sphère S2. Le lecteur intéressé par la surface de Boy pourra en trouver une maquette 3d dans une des salles du Palais de la Découverte de Paris, maquette que nous avions fait confectionner par le plasticien Max Sauze, à partir d'un modèle plus rustique, que nous avions réalisé.
...Dans ces opérations de revêtements à deux feuillets les méridiens et les parallèles des objets "s'enroulent sur eux-mêmes". On peut par exemple montrer ce qu'il advient des "parallèles" du tore (liés au plongement également représenté) :
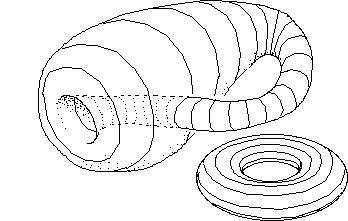
...Dans ce plongement du tore les courbes parallèles ne sont évidemment pas des géodésiques de la surface (sauf le "cercle de gorge"). Situation analogue pour les méridiens du tore, qui sont des géodésiques de son plongement standard :
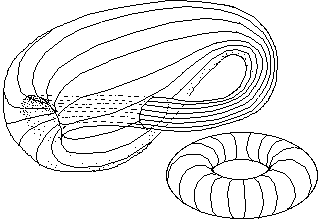
Ci-après, les deux, superposés :
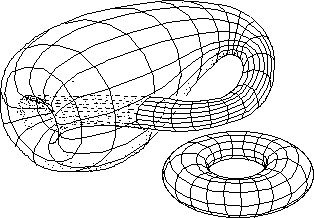
...Nous reprendrons toutes ces choses dans un texte consacré aux retournements de la sphère et du tore, qui sera également intégré au site.
...Cette digression est simplement là pour nous faire comprendre que, dans les illustrations émaillant l'article, les lignes d'auto-intersection de sont nullement l'image didactique d'une quelconque réalité 3d, si l'univers avait une telle topologie, bien sûr.
...Ce papier était une première approche du confinement d'un objet par sa structure conjuguée, sous forme d'une solution analytique, développée à la section 4 . On y trouvera également les premières ébauches des simulations numériques (2d) effectuée par Pierre Midy sur Cray-1.
