...Bien sûr, ce modèle ne gère pas "le reste de la physique". Pour le rendre complet il faudrait adjoindre des variations ad hoc des constantes liées aux autres interactions, forte, faible. Considérons que c'est une idée de plus, à débattre (ce qui est possible, nous le faisons de suite. Pour l'impossible, nous demandons un délai...)

 ...Le détail de ce modèle est à lire dans l'article [Sur ce site: Geometrical Physics A , 6 , 1998] . Pour mémoire nous donnerons les variations des constantes de la physique en fonction de la variable chronologique t .

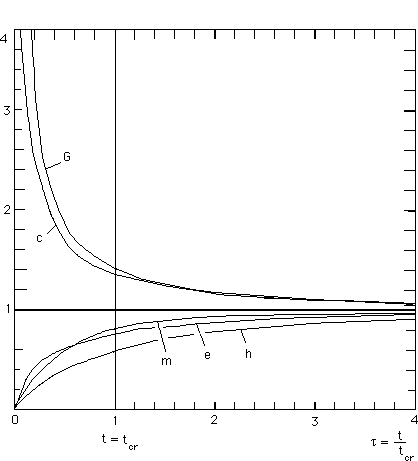
Le temps dans le second univers.

 ...Dans ce qui précède nous sommes partis d'hypothèses purement géométriques, ce qui nous a amené à proposer un système de deux équations de champ, couplées. Nous avons vu que ce système était équivalent au fait d'inverser le signe des masses de la seconde population, bien que les masses m* soient positive.

...Quand on résout ces équations, on donne aux deux métriques des formes particulières, qui ne font que tenir compte de différentes hypothèses. On suppose que la Relativité Restreinte "fonctionne" dans les deux feuillets. Ceci nous amène à choisir une forme particulière de métrique Riemanienne, dite "à signature (+ - - -) ". Puis nous supposons que ces deux univers sont homogènes (que les paramètres, pression, densité, sont les mêmes en tout point de l'espace) et isotropes (que l'apparence de l'univers est la même quelle que soit la direction vers laquelle on se tourne. A l'aide de ces métriques particulières nous pouvons exprimer les tenseurs S et S* puis résoudre les équations, en obtenant en fin du compte des équations différentielles permettant de définir les évolutions de R et de R*, "facteurs d'échelle" des deux univers.

...On fait de même dans la théorie standard, sauf qu'on a une équation de champ unique, l'équation d'Einstein, une seule métrique et qu'on aboutit au bout du compte à une seule équation différentielle. C'est la célèbre équation de Friedmann :

Remarque immédiate : cette équation est invariante lorsqu'on change t en -t , elle est "time-reversible".

...En fait, rien dans notre physique ne nous permet de faire la différence entre le passé et l'avenir. Quoi qu'on fasse on est toujours ramené à une conception subjective du temps. Seuls nos sens nous permettent de faire la différence entre le passé et le futur.

...Une surface possède des géodésiques. Mais il n'y a pas de sens de lecture pour celles-ci. Le choix du sens du temps est arbitraire.

...Les équations différentielles couplées (équations (37-a) et (37-b) du papier [Geometrical Physics A , 6 , 1998] sont également invariantes quand on change t en - t.

...En remontant en amont, on sait qu'on peut repérer deux points conjugués M et M* de nos deux hypersurfaces avec le même jeu de coordonnées. Appelons ces coordonnées (t , z , x , h). On peut alors mener le calcul jusqu'au bout et obtenir les deux équations différentielles finales, couplées (écrivons-les) :

qui sont invariantes si je change t en - t .

A ce stade je peux très bien décider que :  t = t t* = t
ou que :  t = t t* = - t

...Les équations ne définissent aucune orientation temporelle a priori, pas plus que ne le faisait l'équation de Friedmann. Mais alors, que signifient ces variables t et t* ?

Ajout en date de février 2000 :
Entre le moment où j'avais composé ce texte et aujourdh'ui se sont situés tout un lot de travaux nouveaux concernant les trous noirs (ou plutôt allant dans le sens de leur inexistence). A la lueur de ces travaux, je dirais maintenant que les grandeurs t et t* ne sont que des coordonnées, et rien d'autre. Le fait qu'on décide par exemple que t* = -t ne signifiera absolument pas que si on passe du feuillet F au feuillet gémellaire F* on va se mettre à vivre "à rebrousse-temps". Dans ces nouveaux travaux ainsi évoqués on s'intéresse tout particulièrement à la manière dont les deux feuillets pourraient se trouver mis en communication (pendant un très bref instant, le temps d'un transfert hyperspatial de matière du feuillet F au feuillet F*). Qu'arrive-t-il alors à cette matière qui s'échappe vers "le versant rétrochrone de notre univers" ? Chemine-t-elle à contre-temps ?

...Elle évolue dans le feuillet F* où la coordonnée temps se trouve inversée. Mais en transitant d'un feuillet à l'autre, une masse témoin a suivi une géodésique. Sa "montre de bord" (c'est à dire son temps propre" continue de progresser vers le futur. Qui plus est cette particule témoin pourrait théoriquement réemerger dans F après avoir effectué un trajet en empruntant "les couloirs du gémellaire". Serait-ce à dire que cette pérticule témoin pourrait réemerger avant d'être partie?

...Non pas. A aucun moment son cheminement n'a été "rétrochrone". Mais alors, quelle est la nature ontologique de cette inversion du temps. Attention, il ne s'agit que de l'inversion de la coordonnée temps, pas du temps propre. En s'inspirant des travaux de Souriau (Structure des Systèmes Dynamiques, 1974, Dunod, page 198, équation 14.67) on sait qu'inversion de la coordonnée temps et inversion de la masse (et de l'énergie) sont des phénomènes conjoints. L'inversion du temps résulte de l'action des "composantes antichrones du groupe de Poincaré". Quand à l'inversion de la masse et de l'énergie elle découle de l'action du groupe sur son espace des moments.

...Ainsi "cheminer pendant un temps dans un feuillet où la coordonnée temps t* est inverse de la nôtre" signifie simplement que pendant ce temps où elle est "en plongée dans le jumeau" une masse témoin m contribue négativement au champ de gravité (relatif au particules restées dans son feuillet d'origine).

Iinverser le temps équivaut à inverser l'énergie et la masse.

Nous avons vu que nos particules de matière-fantôme se comportaient comme si elles possédaient une masse négative. On peut dire que si deux particules qui interagissent ont des masses positives, mais des flèches du temps inverses, elles se repoussent, gravitationnellement. Dans le papier : J.P.Petit and P.Midy : Geometrization of antimatter through coadjoint action of a group on its momentum space. 3 : Twin group. Matter anti-matter duality in the ghost space. Reinterpretation of the CPT theorem. [Sur le site: Geometrical Physics B, 3 , 1998.] nous avons tenté de dégager la structure de groupe qui sous-tendait cette géométrie gémellaire. Nous sommes arrivés à la conclusion que les deux feuillets étaient liés par des relations de symétrie et qu'en particulier leurs flèches du temps étaient opposées. On rejoint alors l'idée initiale d'André Sakharov et sa théorie des univers gémellaires.