Twin matter against dark matter
J.P.Petit, P.Midy & F.Landsheat
International Conference on
Astrophysics and Cosmology
”Where is the matter ?”
Marseille, 2001 june 25-29
![]()
Abstract
...Recent 3d mapping of dark matter (Fort
and Meillier 1999) implies the existence of "dark clusters", which
would be exclusively composed by dark matter. Exploring a new way, one assume
in a first step that dark matter owns a negative mass and energy and shows
it fits observational data : VLS, spiral structure formation, confinement
and rotation curves of galaxies, gravitational lensing. By passing it suggests
a possible scenario for galaxies' formation. A new geometrical description
of matter-dark matter couple is proposed, through a two-points cover of a
M4 manifold, forming a two folds ( F , F ) space-time structure. The
fold F is called the twin fold (Sakharov 1967) and the matter it contains
is called the twin matter. In such geometrical background matter and (negative
mass and energy) twin matter interact only through gravitational forces, the
last one being optically invisible from our fold of the Universe. Our world
and the twin world being disconnected this prevents encounters between opposite
energy particles. Group theory shows that matter-antimatter duality holds
in the twin universe and that it is filled by CPT and PT-symmetrical matter,
so that the Feynman PT-symmetrical antimatter is nothing but the antimatter
of the twin fold, while CPT-symmetrical composes its matter, going backwards
in time, enantiomorphic, and owing opposite electric charge. We present a
coupled field equations system. Exact solutions are derived, including spherically
symmetric one, similar to Schwarzschild. We get conjugated geometries, with
opposite scalar curvatures R = - R. It is shown that the presence of
twin matter in an adjacent portion of space creates induced
local negative curvature in our fold, which goes with negative gravitational
lensing effect. Comparizon with observational data is discussed. As a cosmological
model the couple universe-twin universe shows different histories. The twin
matter acts as a repulsive matter and accelerates the expansion of our universes,
playing the role of a “cosmological constant”. Conversely the expansion of
the twin in slowed down. For radiative era we develop a variable speed of
light model, which ensures the homogeneity of the early univers : the inflation
hypothesis is no longer necessary. Time’s nature is discussed. In Newtonian
approximation, joint gravitational instability theory is developed, based
on two coupled Jeans-like equations. Starting from the TOV equation, we build
a model of sleaking neutron star (SNS) in which a central space bridge, connecting
fold F and F, drains off any excess of matter in the twin space, preventing
geometrical criticity. This challenges black hole model, whose validity is
contested on theoretical grounds.
1 - Introduction. Dark matter is now the unique answer to any astrophysical problem. It ensures the confinement of galaxies, shapes their rotation curves, is responsible on the observed strong gravitational lensing effects, shapes the VLS. A today's specialist in galactic dynamics deposits ad hoc dark matter distribution in each galaxy, in order to fit its observational rotation curve, which is now known with good accuracy, due to the efforts of many observers. But galactic dynamics, as conceived by men like Oort, Chandrasekhar, based on the joint resolution of Vlasov and Poisson equations is now an empty box. The law of physics become fuzzy. In order to explain the problem due to new evaluation of the Hubble's constant, theoreticians reactivate the so-called cosmological constant, while physicists wonder where the "repulsive power of vacuum" comes from. Astronomy shows a strange paradox : the observations become more and more precise, richer and sophisticated each year but nobody knows how a galaxy works and forms. The contemporary epoch is devoted to the discovery of the invisible. As the Machos' research finally failed, after ten years' effort, all speculations are now considered, the goal being to discover what dark matter is made of. Several research teams stake on the (indirect) observation of the neutralino, an exotic particle which is supposed to come from the supersymmetry's world and depends on 120 free parameters (seven, the specialists say, with some convenient and reasonable assumptions). Active search of "astroparticles" starts everywhere, in new labs. In France, Fort and Meillier have recently "mapped" dark matter, basing their study on the observed gravitational lensing effects. Since 1989 they have built an adequate method. They presented [1], march 2000, a 3d map of some portion of the Universe, showing the invisible, the underlyling dark matter. But in 1994 the first discrepancy arises [2]. The two French researchers discover a portion of the sky where their analysis locates a large concentration of matter, desperately dark. In 1998 a new picture, from the CFHT shows the same phenomenon, near by the Abell 1942 galaxies' cluster. See figure 1.
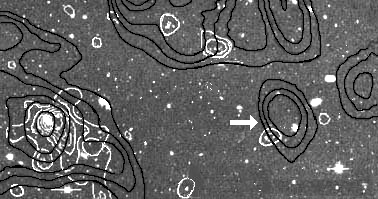
Fig.1 : Arrow : the (dark) portion
of the sky where the analysis of Fort and Meillier locates a concentration of
dark matter equivalent to 5 1014 solar mass. The border of the exotic dark matter cluster is indicated by closed
dark loops.
...Puzzled, in
order to clear up the problem, they decide to make new observations in
different light frequencies. But this result is confirmed. If their method is
correct a "dark cluster" lies there. As said Fort, interviewed in
june 1999 [2] : "It seems difficult to me to
think that such huge concentration of dark matter would have captured no galaxy
nor gas". As their study refers to a square degree portion of the sky, it
means than astrophysicists will have, in the future, when the whole sky will
have been mapped with their method, to deal with some 10,000 "dark
clusters". This shows that the question of the dark matter is far to be
clear, today. There is a room for challenging approaches.
2) What about negative masses and
energies ?
...Can Universe
contain both positive and negative masses, obviously owing negative energy ?
Today, all speculations about "exotic particles" are allowed. In a
first step let us assume than our Universe is a mixture of positive and
negative masses and see what happens. We can assume that this negative energy
matter corresponds to some sort of an exotic matter, which would interact with
ordinary matter only though gravitational force, emit and capture no photon
(i.e. this matter would be dark and invisible). Later we deal with another
hypothesis, implying an "exotic geometry" (section 8). .Let us choose
the laws of interaction (which will be justified latter too, in section 12).
- positive masses attracts
each other through Newton law.
- negative masses attract each other through Newton law.
- a positive mass m and a negative mass m repel each other through
"anti-Newton law".
...Former results were published in
Nuevo Cimento in 1994 [3]. The two population separate,
experiencing joint gravitational instabilities.
3) 2d simulation of the VLS in terms of interaction of two populations,
with opposite masses.
...In 1970 Zel'dovich proposed his well-known pancakes theory [5]. The pancake effect was first demonstrated by Doroshkevich and al.[6], Klypin and Shandarin [7] , and Centrella & Mellot [8]. Mellot and Shandarin (1990)] gave an elegant demonstration of the effect by using two-dimensional computations that afforded considerably better resolution for a given particle number [9]. Shandarin, Kofman and Pogosyan presented a powerful semi-analytic method for predicting the positions of pancakes from the initial conditions [10] & [11]. More recently Mellot used a 3d set of 643 particles, with periodic boundary conditions. From Mellot, the density fluctuations remain small. As pointed out by Peebles [12] "This cannot be the whole story, for the pancakes found are a transient effect : with increasing time the mass in the pancakes drains into clumps that are concentrated in all the three dimensions. This means that if the local sheet of galaxies was a pancake, it must have been formed recently". Then Peebles asked : " could there be a second generation of pancakes that formed out of the first generation ? " But he concluded immediately : " This does not follow from the analysis given here, for it depends on the continuity of the velocity field that allows to write down a series expansion for the evolution of the relative positions. After the formation of the first generation of clumps, which might be the galaxies or their progenitors, the velocity field in general does not have the coherence length, and the analysis from the continuity does not apply". As a conclusion the pancake theory cannot describe, in the present state, the observed large structure, so that let us try something else : we take initial condition with uniform mass distributions for normal matter (that we simply call matter) and twin matter. Given the mass density of the matter and the (negative) mass-distribution of the twin matter, we choose for initial conditions :
![]()
At this level, just see what happens. We have performed 2d numerical
simulations with two sets of 5000 mass-points, that are supposed to represent
some clusters of matter and twin matter, with masses M>0 and M <0
(which means that ½M½ = 64 M). We give these two sets
maxwellian distributions of 2d thermal velocities with <V> = 4
< V > . We neglect the expansion phenomena (it would be very difficult to
deal with, for we do not know how to describe gravitational force in an
expanding universe). The result is the following. The more massive population,
the twin matter's one, whose Jeans time is eight times shorter than the other
one’s runs the game and forms clumps, through gravitational instability, that
repel and confines the other population in the remnant place. We get a
2d-cellular structure. The characteristic birth time of the whole structure is
close to the Jeans time of the heavier population (of the negative mass matter,
the twin matter).

Fig. 2 : Results of simulations performed by F.Lansheat.
Left : twin matter
clumps. Right : matter structure.
.These 2d simulations are remarkably stable in
time. Of course, they are 2d simulations, so that we must consider this result
as an illustration of an idea. 3d simulation are far beyond the capabilities of
our computational system. But we think that, in 3d, we would get 3d cells,
looking like joint soap bubbles, centred around negative mass clusters. The
general pattern depends on the initial conditions. The larger the twin matter
temperature, the bigger are the clumps. This approach, aiming at a modelisation
of the very large scale structure of the Universe, is fundamentally different
from the classical approaches based on the dark matter. In classical
matter-dark matter systems, stability is problematic : gravitational
instability, by rising up the density locally, increases the thermal velocities
and makes the observed structures to disappear in time. The system with two
repelling populations is qualitatively different, each population creating a
potential barrier for the other one. This explains the great stability in time
and space : the cells of matter keep the clumps of twin matter in place, and
the clumps prevent the dissipation of the cellular structure.
...On figure 5, call d the diameter of
a cell and f the diameter of a clump. For different given
initial conditions, and randomized initial positions of mass-points, the number
of clumps nc (and cells on the screen) does not change so much. The
standard deviation obeys (a). ...Same thing
for the masses and diameters of the clumps (b) , (c)
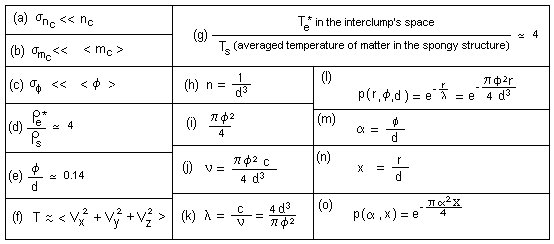
We can examine some
features, for this peculiar numerical computation. Matter forms a cellular
structure. Call rs the mean mass
density of matter in that structure. Outside the clumps, the twin matter has a
constant density (subscript e, for "external"), corresponding to (d)...The mean diameter of the clumps, compared to the mean diameter of the
cells, obeys (e). We define some sort of
"pseudo-temperature", as a measure of the mean kinetic energy in
these 2d gazes (f). Where we have (g).
T refers to a temperature (of a gas of matter) before galaxies'
formation. Can we estimate the effect of these hypothetic twin matter clumps on
the light coming from distant sources ? A photon, located in our fold of the
universe, cannot be captured by a twin matter particle, on pure geometric
grounds. But twin matter clumps act on the photon’s paths by negative
gravitational lensing. Can the presence of twin matter clumps be evidenced by
some cosmological test ? We can build a rough evaluation, taking a
non-realistic situation where the universe is described as euclidean and
steady, that would fit moderate distances. The diameters phi of the twin
matter clumps are very similar. As seen before, the standard deviations are
weak so that we can figure space, over large distances, as a regular
distribution of cells, with a spheroidal clump nested at the centre of each
cell, and we can take the same diameter
or all clumps. Call
n the number of density of the clumps, assumed to be constant over space (h). A
photon travels with the velocity c. The cross-section of a clump is (i). The
encounter frequency is (remember that the photon cannot be absorbed by the
clumps) (j). The mean free path is (k).
Can we size the number of galaxies whose image would be altered by
negative lensing effect, at a given distance r ? From kinetic theory we know
how to compute the probability to observe a free path of a given length r. It
is (l). Let (m) + (n) then (o). p
strongly depends on the value of a .The probability et to get a gravitational lensing effect is 1 - p , which correspond to the
curves :
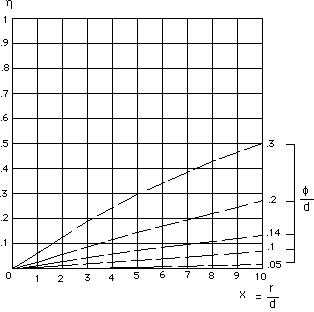
Fig. 3 : probability to observe anti-lensing (negative lensing) effect
versus distance, for different (rrelative) values of the clumps'diameter
...The computational results, presented in the
paper, correspond to the value of this relative diameter of clump's diameter versus celle's diameter equal to :
![]()
But dissipative processes may occur
in the clumps, that could drastically reduce their diameter, transforming these
objects. The today’s averaged ratio (twin matter density / normal matter
density) IrI /r is 64. If clumps transform into relatively small objects we could
expect to get unaltered images from distant sources (quasars, galaxies). A
cluster of galaxies, roughly speaking, acts as a biconvex lens. A twin matter
clump would act as a concave lens. The images of distant galaxies, through such
gravitational lens, should appear smaller, fainter and more numerous as pointed
out by Peebles (ref. [12], page 311).
4) A possible schema for galaxies'
formation.
......When the
cells form, the two populations separate. The twin matter clumps repel an
compress the ordinary matter, forming the cell's walls. In these walls the
temperature grows and this peculiar geometric configuration is optimum for fast
radiative energy dissipation. The subsequent decrease of temperature in the gas
of the walls makes them gravitationally unstable, and proto galaxies form. In
the same time twin matter takes place in the inter-galactic space and exert a
counter-pressure on them, which ensures their confinement.
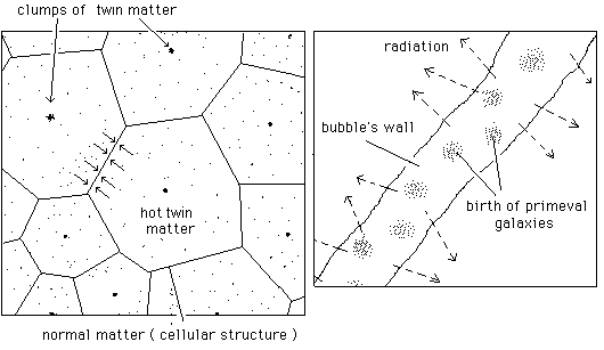
Fig. 4 : A possible schema for galaxies’
formation. Left, matter is compressed by repulsive effect of twin matter’s
clumps, located at the centre of the cells. Right : fast radiative cooling of
this matter, which becomes unstable an forms young galaxies.
..As wee see this model bring new
insights of astrophysical problems and deserves 3d computations. Let us look
more closely to the question of the confinement of galaxies.
5) Galaxies confined by surrounding twin
matter counter-pressure.
... ...Everybody
knows that no self-consistent model of a galaxy exists. Their description
remains purely empirical. The galactic dynamics is a complete mystery. Today,
theoreticians spray ad hoc distributions of unidentified dark matter, in order
to fit gas rotation curves, that's all. Let's try to modelize this through the
interaction of matter and surrounding twin matter. We start from the galaxy's
density profile as given by Myamoto and Nagaï [13] :
![]()
...Around, we install a succession of
elliptic twin matter shells, owing same eccentricity, whose density grows from
the centre to infinite (see their density profile, figure 5, below). The
Newtonian field created by such thick shell is given by simple analytic formula
[14]. ...Now we add the galaxy, which
reinforces the gravitational field, mainly close to the centre, where the
pressure force balances the field. As shown on figure 3 the gravitational force
has a confining z-component. Such a phenomenon might explain the anomalous
large z-velocities, evidenced by Bahcall ( [16] and [17] ) for K stars. A
complete and systematic study should be carried out by this method. Finding
these large velocities, Bahcall concludes that some dark matter must be present
in the disk of the galaxies. According to our model, that could be due to the
repulsive effect of
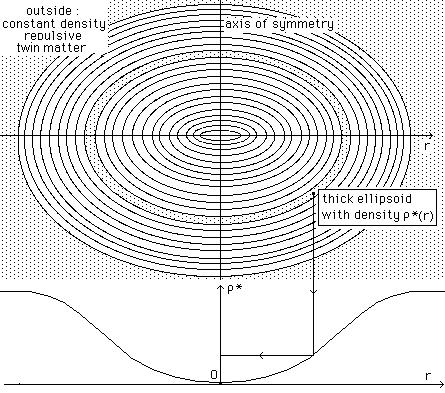
Fig. 5 : Ad
hoc twin matter distribution, for 3d confinement.
The density is constant between successive homothetic flat ellipsoids.
surrounding
repulsive dark matter : an alternative interpretation. In general, starting
from observational data, people can compute the distribution "conventional" dark matter in space. Similarly, from same
observational data, it is possible to build a corresponding distribution of repulsive repulsive dark
matter, through the method presented above. The local intensity of the
gravitational field depends on the chosen distribution. Here we have used a
system of concentric shells figured as a set of thick ellipsoids with the same
eccentricities (but eccentricities might be different : any kind of
distribution of repulsive repulsive dark
matter can be managed by this method). We get a rotation curve, corresponding
to gas orbiting in the z = 0 plane, good-looking, as shown on figure 7. The
scale, shown, corresponds to figure 8.
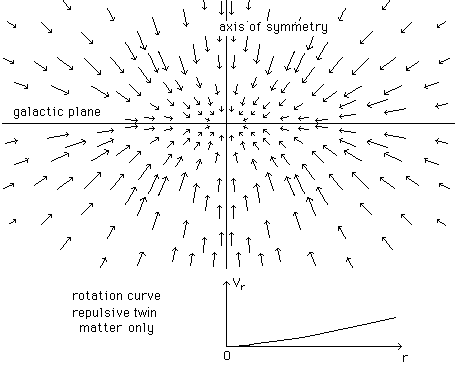
Fig. 6 : Confining
field and corresponding rotation curve
(circular velocity of m = +1
test-particle)

Fig. 7 : The
galaxy, plus its environment of hot twin matter.
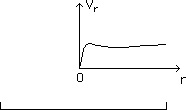
Fig. 8 :
Combining the two fields we get a good-looking galactic rotation curve.
...The repulsive
dark matter environment acts as a "box". The flatter that box, the
stronger the corresponding impact on the z-confinement effect is. With the
chosen parameters, the z-confinement enlarges the velocity of the stars located
at z = 0.2 dg (where dg is the overall diameter of the galaxy) by a
factor 1.4. By the way, the presence of repulsive material at the vicinity of
the galaxy explains the steep fall of the density at the periphery of the gas
disk. The global gravitational field (acting on the repulsive dark matter)
tends to enlarge the hole. But its pressure gradient balances it : if the
galaxy was removed, the repulsive dark matter fills the hole. The repulsive
dark matter distribution was shaped on empirical grounds, through numerous
trials and various sets of massive ellipsoids. It could be a starting point for
full 3d numerical simulations, which are beyond our today’s computational
possibilities. Moreover, we believe that a more elegant model could be built,
using Vlasov equations, coupled with Poisson equation. By the way, are
spheroidal galaxies confined in the same way, nested in spheroidal holes
managed in constant density twin matter ? Isin’t contradictory the the Gauss
theorem which would tend to give a zero Newtonian field inside the hole? To get
the answer, go to section 18.
6) Spiral structure.
...Since many
years astrophysicists try to understand what produces the spiral patterns of
the galaxies, and if it is a transient phenomenon or not. In 1959 Lindblad [18]
suggested that the spiral arms could be density waves. Later Lin and Shu
regarded the spiral pattern as a wave pattern [19]. Their analysis, based on
the set of the equations of Vlasov and Poisson, used a perturbation method,
which could not provide non-linear patterns, so that they imagined that some
spiral perturbation could appear in the star population and trigger the gas,
whose strongly non-linear response could explain the observed Grand Design.
Toomree gave later theoretical arguments supporting this idea [20]. At the
begining of the seventies, Toomree explored another interpretation of the spiral
origin : the action of a companion [21]. This was extended later ( [22] and
[23]). In effect, some of the nicest examples of global spiral structures have
close companions, like the well-known M51 [24], but not all the galaxies with
global spiral structure have a close companion. Typically, a galaxy is composed by 1011 stars. In
numerical simulations, one deals with 104 to 106
interacting objects, considered as self-gravitating groups of stars. Most of
the simulations tried so far were 2d, and neglected z-motions. Some fully
calculations have been attempted [25]. A number of early simulations verified
that isolated disks could be axisymmetrically unstable : a bar forms in the
early stage of the evolution and, with relatively small change of amplitude, shape
and pattern speed, and survives the end of the calculation. But, if spiral
pattern appears, it tends to disappear quite rapidly. Transient spiral
structures appears in the initial stage of each run but, unless the bar
instability has been suppressed, it heats the disk to temperatures suffocating
the spirals [26]. The sweedish school
has been pionneer in the study of interacting galaxies device [27] . See also
reference [28]. But all the spiral galaxies are not interacting galaxies, so
that the problem remains unsolved. In other works, based on numerical
simulations, people studied "impulsively perturbed galaxies",
omitting to describe the origin of the perturbation [29]. As a conclusion we still do not have a
convincing model explaining why many galaxies have a spiral structure, barred
or not, and if it is or not a transient phenomenon. Through analytic methods or
numerical simulations many people suggested different mechanisms, evoked. Some
think now that the solution requires a better knowledge of the physics of the
galaxy, including dissipative process. Such process could cool the material of
the spiral arms and prevent their dissipation, but the problem is to justify
how these dissipative processs occur. In 1972 Toomree wrote [30] :
"Happily it remains a subject where it makes sense to start almost at the
beginning". That is what we are
going to do. This work was initiated by Frederic Landsheat at the begining of
the nineties, through 2d simulations. To deal with border conditions, we used a
classical periodical lattice. With such method (see discussion about spatially
periodic systems in F.Bouchet and L.Hernquist, reference [31] and F.Bouchet, L.Hernquist and Y.Suto, reference [32] ) we obtained in 1992 good looking films showing the birth of a barred
spiral (figure 9) with 2 x 5000 mass-points. The twin structure is not shown. As for VLS, the good
surprise was the remarkable stability of the Grand Design, over 50 turns. Same
explanation : the surrounding repellent twin matter forms a potential barrier
which prevents spiral arms dissipation. On figure 9 the evolution of the
momentum of the galaxy, versus the number of turns. When the grand design
forms, the strong observed slowing down is due to dynamical friction. Then,
after few turns, tidal effects dominate.
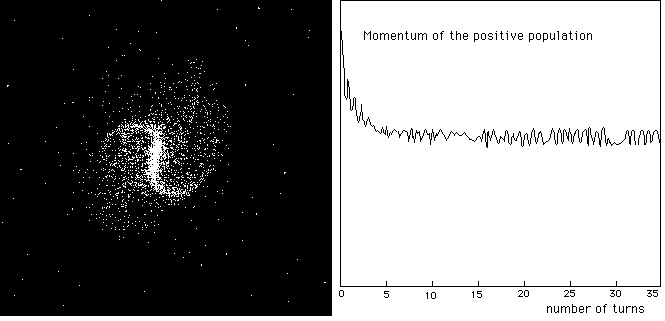
Fig. 9 :
Barred spiral (J.P.Petit & F.Landsheat, 1993)
...These images were encouraging, but the work was stopped because Landsheat, who worked at DAISY, Germany, had to join a new lab where he could not use an adequate computational system.
