Proposition de séminaire en cosmologie
2 novembre 2006
Géométrisation
du modèle cosmologique d’Andréi Sakharov
J.P.Petit
& G.D’Agostini
Le prix Nobel Andréi Sakharov est peu connu pour
ses travaux dans le domaine de la cosmologie ( [1], [2], {3] ). Un des auteurs
( [7], [8], [9], [10] , [11] ) a travaillé dès 1977 dans la même voie, en
ignorant ce travail dont il ne devait prendre connaissance qu’en 1984 au moment
de la parution en France d’un ouvrage intitulé « Andréi Sakharov, œuvres
scientifiques » [4], initialement publié en langue anglaise en 1982 [5].
En définissant schématiquement ce modèle,
impliquant une T-symétrie, Andréi Sakharov expose sa préoccupation
première : rendre compte de l’absence d’antimatière dans notre univers
observable. Après avoir envisagé une symétrie T, Sakharov opte pour des univers
CPT symétriques [6].
Nous allons traduire cette idée géométriquement en
utilisant les outils suivants :
-
Groupes
dynamiques
-
Espace des
moments ( dual de l’algèbre-de-Lie du groupe )
( référence :
Structure des Systèmes Dynamiques, J.M.Souriau, 1972 [12] )
Partons du groupe de Poincaré, groupe d’isométrie
de l’espace de Minkowski. Le nombre des composantes du moment est égal à la
dimension du groupe, c'est-à-dire dix. Ces
composantes sont alors regroupées comme suit :
-
Une
composante qui est l’énergie E
-
Trois composantes
qui composent le vecteur impulsion.
- Trois composantes constituent ce que Souriau appelle le « passage »
- Les trois autres forment le « tournoiement ».
( cette
approche permet de faire apparaître le spin en tant qu’objet purement
géométrique, voir référence [12], page 181 ).
Le groupe de Lorentz possède quatre composantes
connexes.
-
La première,
la composante neutre du groupe, n’inverse ni l’espace, ni le temps.
-
La
deuxième inverse l’espace ( P-symétrie ) mais pas le temps.
-
La troisième
inverse le temps mais non l’espace ( T-symétrie)
-
La quatrième
inverse l’espace et le temps : ( PT-symétrie ).
Souriau regroupe les deux premières composantes du
groupe de Lorentz pour former ce qu’il appelle le sous-groupe orthochrone Lo . Les éléments de ce
sous-groupe, agissant sur un mouvement donné, conservent l’orientation du
temps. Les composantes restantes constituent le sous-ensemble antichrone LA , dont les
éléments inversent le temps ( T-symétrie ).
Construit à partir du groupe de Lorentz en y
adjoignant les translations spatio-temporelles le groupe de Poincaré comporte
également quatre composantes connexes.
L’étude de l’action du groupe de Poincaré complet
( avec ses quatre composantes ) sur son espace des moments montre que la
T-symétrie entraîne l’inversion du signe de l’énergie (référence [12], page
197, « inversions d’espace et de temps », relations (14.67). )
Kaluza a montré que le fait de doter un point
matériel relativiste d’une charge électrique était équivalent à inscrire son
mouvement dans un espace doté d’une dimension supplémentaire, du type
espace :
t , x , y , z , z
Un point de cet « espace de Kaluza » correspond
alors au vecteur :
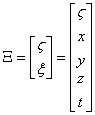
Le groupe dynamique associé à cette géométrie est
l’extension centrale du groupe de Poincaré. On peut représenter matriciellement
l’action de ce groupe sur l’espace de Kaluza selon :
![]()
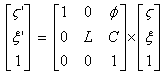
L, matrice (4,4)
est l’élément du groupe de Lorentz, qui est de dimension six. C est le quadrivecteur correspondant à
une translation spatio-temporelle :
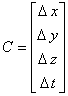
f est un scalaire. Cette
extension centrale du groupe de Poincaré est de dimension 11. C’est aussi par
définition le nombre des composantes du moment. Ainsi le fait d’inscrire le
mouvement du point matériel relativiste dans un espace muni d’une dimension
supplémentaire, la dimension de Kaluza, dote le moment d’une composante supplémentaire,
scalaire :
la charge électrique q
L’action de ce groupe sur son espace du moment comporte
l’apport d’une relation supplémentaire qui traduit la conservation de la charge
électrique :
q’ = q
Pour faire apparaître une C-symétrie il faut
passer à un groupe comportant huit composantes connexes, dont l’élément
s’écrira :
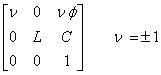
En étudiant l’action du groupe sur son moment,
l’action sur la charge électrique devient :
![]()
On retrouve ( référence [13] Géométrie et
Relativité p.413 ) l’identité entre conjugaison de charge et inversion de la
dimension de Kaluza. Nous avons donc sous les yeux la traduction géométrique
claire de la C-symétrie.
Comme nous l’avons dit, le groupe de
Poincaré :
![]()
contient des éléments réalisant les symétries P ,
T et PT. Considérons le sous-ensemble Lo,
orthochrone, du groupe de Lorentz.

qui est une façon commode de représenter l’élément
du groupe de Lorentz en dégageant les éléments du sous-groupe orthochrone ( m = + 1 ) et les éléments du sous-ensemble
antichrone ( m = - 1 ) . On
peut réécrire l’élément du groupe de Poincaré selon :
![]()
Les composantes antichrones du groupe de Poincaré,
ou de son extension centrale impliquent l’existence de mouvements de particules
dotées d’une énergie négative. Leur rencontre avec des particules d’énergie
positive se traduirait par une complète annihilation.
L’univers tel que nous le concevons se compose de
particules à masse non nulle et de particules à masse nulle, les photons (sans
préjuger de la nullité ou de la non-nullité de la masse des neutrinos). Toutes
ces particules ne sont que des mouvements particuliers du point matériel
relativiste.
Si on accepte de faire agir l’ensemble des
composantes du groupe ceci suggère l’existence :
-
De particules
à masse non-nulle, d’énergie négative
-
De photons
d’énergie négative
Du point de vue de la physique il semble difficile
d’envisager une cohabitation d’objets à énergie positive et de leurs
T-symétriques, à énergie négative. D’où l’idée qui fut la nôtre, consistant à envisager
un espace des mouvements non-connexe.
Comme Sakharov nous prendrons pour base un univers composé de deux feuillets CPT symétriques par rapport à une
![]()
Nous pouvons traduire cette idée en termes de
groupe en faisant intervenir un indice de feuillet
f = ± 1
![]()
Considérons le groupe suivant et son action sur un
espace pentadimensionnel non-connexe.
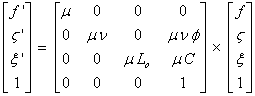
Dans cette construction la CPT-symétrie (
inversion de z et de x ) va avec
l’inversion de l’indice de feuillet ( f
→ – f ).
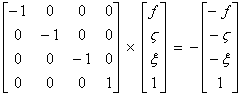
La calcul de l’action coadjointe débouche
sur :
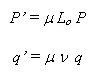
P étant le quadrivecteur impulsion-énergie.
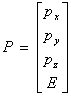
Si l’espace des mouvements correspondant à f = 1 contient les particules à énergie
positive, l’élément du groupe correspondant à
m = - 1 inverse la coordonnée f ( changement de feuillet ), l’énergie E, l’impulsion p , la
charge électrique q et entraîne une
CPT-symétrie.
La dualité matière-antimatière ( C-symétrie ) est
présente dans chacun des deux feuillets.
On a donc une description géométrique du modèle
proposé initialement par Andréi Sakharov.
Nous pouvons maintenant essayer d’apporter des
précisions sur l’espace-frontière joignant les deux feuillets ( f =
+1 et f = -1 ). Une des dimensions
doit disparaître.
On trouve dans notre univers des mouvements se
déduisant l’un de l’autre par P-symétrie. Exemple : deux photons de même
énergie mais d’hélicités inverses ( phénomène de polarisation de la lumière ).
La C-symétrie est également à l’œuvre dans notre
univers ( présence avérée d’antimatière, que cela soit dans les rayons cosmique
ou dans les collisionneurs ).
Mais aucune expérience ou observation n’a permis
de mettre en évidence l’existence de particules d’énergie négative.
L’énergie est un scalaire lié à l’invariance par
translation temporelle. Dans l’espace-frontière, lien entre les deux feuillets,
c’est donc la coordonnée temps qui disparaît.
On a deux feuillets pentadimensionnels, deux
espaces de Kaluza ( où la cinquième dimension est du genre espace ) dotés de la
métrique :
ds2 = c2 ct2 – dx2 – dy2 – dz2 –
dz2
de signature :
( + - -
- - )
L’espace-frontière qui les joint a pour métrique :
ds2 = -dx2 – dy2 – dz2–
dz2
de signature :
( - - - - )
Cet espace-frontière est euclidien.
Ce qui correspond schématiquement au dessin de la
figure ci-après :
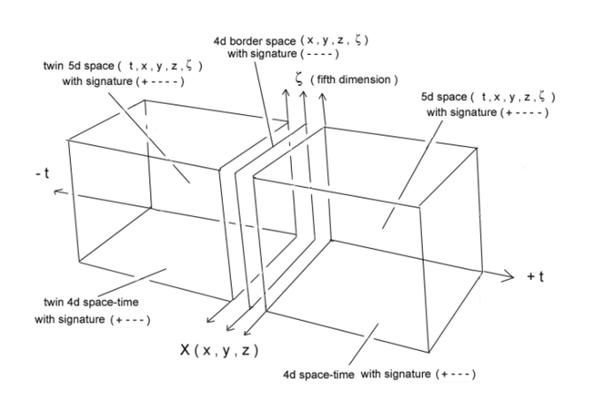
Le modèle de Sakharov ( deux feuillets d’univers CPT symétriques )
L’univers
frontière entre les deux est euclidien
References :
[1] A.Sakharov : "CP violation and baryonic
asymmetry of the Universe". ZhETF Pis'ma 5 : 32-35 (1967) : Traduction JETP Lett. 5 : 24-27 (1967)
[2] A.Sakharov :
"A multisheet Cosmological Model" Preprint Institute of Applied
Mathematics,
[3] A.Sakharov : "Cosmological Model of the
Universe with a time-vector inversion". ZhETF 79 : 689-693 (1980) : Traduction in Sov. Phys. JETP 52 : 349-351 (1980)
[4] Andréi Sakharov, oeuvres scientifiques, Editions Anthropos,
France, 1984 ( épuisé )
[5] Andrei Sakharov, scientific works, Marcel Dekker Inc Ed. 270
Madison Avenue, NYNY 10016
[6] Andréi
Sakharov. Les antiquarks dans l’univers. Communication commémorative pour le
60° anniversaire de N.N. Bogolyubov, Nauka, Moscou, pp. 35-44.
[7] J.P.Petit : "Univers énantiomorphes à flèches du temps
opposés", CRAS du 8 mai 1977, t.285 pp. 1217-1221
[8] J.P.Petit : "Univers en interaction avec leur image dans le
miroir du temps". CRAS
du 6 juin 1977, t. 284, série A, pp. 1413-1416
[9] J.P.Petit : Twin Universe Cosmology : Astronomy and Space Science 226 :
273-307, 1995
[10]
J.P.Petit : The missing mass problem. Il Nuovo Cimento B Vol. 109 July
1994, pp. 697-710
[11] J.P.
Petit, P.Midy & F.Landsheat : Twin matter against dark matter.
Intern. Meet. on Atrophys. and Cosm. "Where is the matter ? ", Marseille 2001 june 25-29.
[12] J.M.Souriau, Structure des Systèmes Dynamiques, Editions Dunod,
1970. English translation in : Structure of Dynamical Systems, Birkhauser Ed.
1999
[13] J.M.Souriau : Géométrie et relativité. Hermann Ed. 1964
|
Cette lettre est restée sans réponse.
Retour vers Nouveautés Retour vers Guide Retour vers page d'Accueil