6) The choice of a time marker.
In the
[ t , r , q , j ] coordinates, corresponding to the
line element (25) the determinant of the metric is :
(34)
![]()
which vanishes
when r becomes zero. Anyway, in 1924, Eddington [10] showed that the nullity
of the metric was coordinate-dependent. Let us first return to the initial form
(35)
![]()
Insist
on the fact that the choice of coordinate system is a purely arbitray, for the
metric, solution of the tensor-form equation
(36)
S = 0
is basically
coordinate-invariant. We decide that particles follow geodesics. The arbitrary
chosen coordinates brings the physical significance of this geometric solution.
We can choose x° = ct, c being a constant. But we can choose another frame of
reference. It is up to us. The only requirement, for a chosen chronological
marker x°, or t , x , is that the metric would be asymptotically euclidean :
(37)
![]()
or :
(38)
![]()
as expressed
in cartesian coordinate system. Remember that a riemanian metric is euclidean
if one can find a system of coordinates where the line-element quadratic form
has constant coefficients. The set of the signs is the signature.
If this last is ( + - - - ) this is a Minkowski's metric.
(39)
![]()
being identified to an elementary distance, it seems a reasonable requirement to impose the metric to be asymptotically euclidean "at large distance", whatever the chosen definition for such a distance ( r or r , from above) is.
The definition of the "cosmic time" or "space marker", remains a completely free choice. Conversely we cannot modify the proper time s, or, more precisely, the time-interval Ds between two given points of the manifold, for it is basically coordinate independent. In addition, one assumes that particles can travel in both directions, along a given geodesic.
Fig. 12 : The travel of a particle on a given geodesic.
The travel of a test-particle along a geodesic is a phenomenon. Another geodesic of the manifold is supposed to refer to some "external observer, at rest". But rest state depends on the coordinate choice (x°, x1 , x2 , x3) , which is completely arbitrary.
This "external observer" is supposed to be located in a portion of
the manifold where the metric is euclidean, or quasi euclidean, i.e. has the
form (37). Then the rest conditions means that
(40)
dx1 = 0
dx2 = 0
dx3 = 0
For such
a rest-state observer any proper time interval identifies to the associated
arbitrarly chosen "cosmic time interval":
(41)
Ds = Dx°
...The choice of cosmic time being purely arbitrarly, the evolution of the test particle in time depends on this choice. Consider two points A and B, on a given geodesic, which is supposed to refer to an external observer. These points are space-time events. On figure 13 the dotted lines are supposed to refer to constant cosmic time x°.
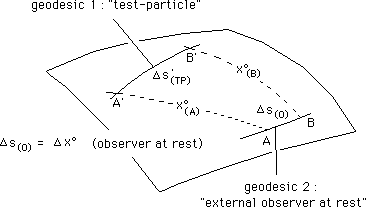
Fig. 13
: An "external observer at rest", "considering" the evolution
of a test-particle
on a geodesic. Cosmic time x°
Consider now another choice x for cosmic time. See figure 14.
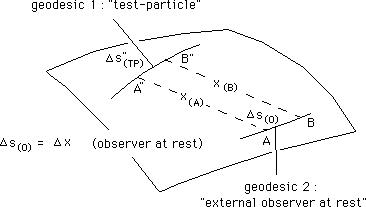
Fig. 14
: An "external observer at rest", "considering" the evolution
of a test-particle on a geodesic. Cosmic time x
Let's precise that dotted lines are not photons' paths. Photons travel on peculiar, null geodesics, which are coordinate-invariant.
We still have Ds(O) = Dx° = Dx but the intervals Ds'(TP) and Ds"(TP) may be fairly differents, although the they refer to the same geodesic, for the couples (A',B') and (A",B") may differ. Basically, they depend on the chosen tim coordinate, or "time marker"..
7) The Eddington's time coordinate change and its extended form.
The following
coordinate change, introduced by Eddington in 1924, an illustration of that
point, is :
(42)
![]()
Then the
line element becomes
(43)
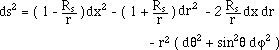
As the gxx term becomes zero on the sphere r = Rs , this last is
an infinite redshift surface (as in the classical Schwarzschild metric line
element). The matrix
becomes :
(44)
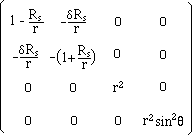
whose determinant
is :
(45)
- r 4 sin2 q
and no
longer vanishes, whatever the r-value is. For reasons that will be explained
lated, let us extend this coordinate change to :
(46)
![]()
Expressed
with the ( x , r , q , j ) coordinate system, the
line element becomes :
(47)
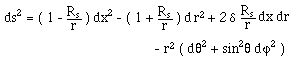
whose
determinant has the same form (44). Notice that the Eddington's coordinate change
of corresponds to d = - 1 value.
We study the geodesics,
using the Lagrange equations, based on the function :
(48)
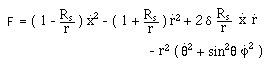
with :
![]()
In addition,
from the line element expression, we have, classically, for material particles
(ds ¹ 0) :
(49)
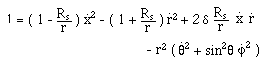
One Lagrange's
equation gives :
(50)
![]()
Consider
the plane geodesic q = p/2 , which gives :
(51)
![]()
Along a geodesic, with respect to the proper time s, the evolution of j, is
monotonic. Another Lagrange's equation gives :
(52)
![]()
i.e. :
(53)
![]()
Combining
to (49), surprizingly, d disappears :
(54)
![]()
Notice that if dr = 0 (null velocity) when r tends to infinite, it corresponds
to l = 1.When r tends to infinite, after (53) :
(55)
![]()
If l
³ 1 , when r tends to infinite, we get :
(56)
![]()
with
![]()
we get
(57)
![]()
In the
[ r , j ] we refind, for non null geodesics (ds
¹ 0), the classical form's differential expression :
(58)
![]()
which provides
patterns of figures 7, 8 and 9. Now we can define a new cosmic time, through
:
(59)
x = ct
...The line element (43) is still asymptotically euclidean. At "large distance" the proper time Ds of a rest observer identifies to the interval Dt.
8) Time intervals for radials paths.
We may
compute the time-interval Dt = Dx/c
of a non zero mass particule, following a geodesic, through the differential
equation :
(60)
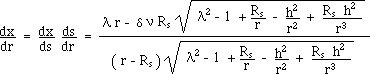
For "radial
geodesics" ( h = 0 ) :
(61)
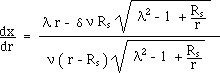
Close to
the Schwarzschild's sphere, we get :
(62)
![]()
l = 1 corresponds to a test particle whose velocity tends to zero at infinite.
Consider
that peculiar case :
(63)
![]()
From (54)
n = - 1 corresponds to (dr < 0) paths.
n = +1 corresponds to (dr > 0) paths.
...Notice that the peculiar Eddington's coordinate change corresponds (for r ³ Rs) to d = + 1 . When we compute the radial travel time Dt of a test particle, with respect to this new cosmic time, we find this last depends on the direction of this movement and on the sign of d, i.e. on the product dn. When it is positive, the travel time of a test particle, along a radial geodesic (r ³ Rs) is finite. When it is negative this travel time becomes infinite.
...As
a first consequence, if applied to the spherically symmetric black hole model,
the Eddington's coordinate change gives a finite free fall time Dt.
When r = Rs the velocity of the particle becomes :
(64)
![]()
A test particle, falling towards the Schwarzschild sphere, reaches it at the velocity c.
9) Light velocity.
Photons
travel on null geodesics, corresponding to :
(65)
![]()
Consider
the velocity :
(66)
![]()
From (65)
we get :
(67)
When r tends to infinite, vj tends to ± c .
When dr
< 0 we have n < 1 . Then, when r = Rs for (d
r< 0) paths :
(68)
![]()
When a test particle falls towards the Schwarzschild sphere, along a radial
paths, it reaches it at the velocity of the light.
To sum up :
(69)
![]()
(70)
![]()
The velocity of the light is different, considering (dr > 0) or (d r< 0) paths.
10) The frame-dragging effect.
Consider
the Kerr metric :
(71)
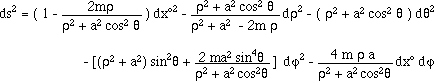
where r
is a space coordinate different from the one defined above. We just reproduce
the equation 7.110 of reference [1].
Compute the velocity of
the photon (ds = 0) for movements which are tangent to circles (q = p/2, r =
constant). We find :
(72)
![]()
i.e. two distinct values. This corresponds to an azimutal frame-dragging and is a property of the Kerr metric. From reference [1], 7.7, "The Kerr solution and rotation"we read :
A very interesting physical effect results from the rotational nature of the Kerr solution; a body in geodesic motion experiences a force proportional to the parameter a reminiscent of a Coriolis force. Loosely speaking, we may think of the rotating source as "dragging" space around with it. In a Machian sense, the sources "competes" with the Lorentzian boudary conditions at infinity in the establishment of a local inertial frame.
Rephrased in terms of Eddington's coordinates, the black hole, considered as the source of the field, induces a radial frame-dragging.
11) Black hole and white foutain.
In section 4 we have suggested a new interpretation of the Schwarzschild geometry
where the Schwarschild sphere, see figure 9, behaves like a throat sphere, linking
two "half space-time folds". We can imagine a similar structure, combining
the two following Schwarzschild geometries :
(73)
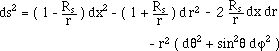
(74)
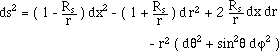
These two are derived from (43), the first line element (73) corresponding to
d = -1 and the second one (74) to d
= +1 . The linking arises no difficulty for d does
not appear in the computation the [ r, j ] representation
of geodesics. See equation (58). We get a couple "black hole-white fountain",
without "central singularity". Matter can enter the black hole, but
not go out. On the other side, matter can flow out of the white fountain, but
not get in. The transit time is finite in one direction, and infinite along
the other one. Computed with the new cosmic time x, the finite transit time
is similar to the one as computed with proper time s. For radial paths :
(75)
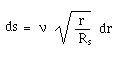
This time is very short. As was shown in this paper, the black hole model is based on a peculiar choice of the coordinates, and especially of the cosmic time. As pointed out in section 6 the choice of the time-marker is purely arbitrary. The classical one gives a quasi steady-state system, where the fall of the matter, poured into the black hole is "frozen in time", with respect to an external observer. But the present paper shows that another choice of the time marker, derived from Eddington's idea, "defrosts" the process. From this point of view black holes, or couples black hole-white fountain, cannot exist as permanent objects, for they can swallow dozens of solar masses per millisecond. So that there still is an open question :
- What happens when a neutron star overcomes its limit of stability ?
12) Representation space.
Before trying to present an alternative project of model, few words about what we could call "representation spaces". In the begining of the paper, we have studied a 2d surface, as defined by its line element. It appeared to be possible to imbed this surface in R3, which gave as isometric representation of this geometrical object. By the way, we mentioned a [r,j] representation.
It is not
possible to give an evident representation of a four dimensional hypersurface
for we cannot draw it and show figures. But the hypersurface can be figured
in many representation spaces, corresponding to various coordinate choices,
for the object is basically coordinate-invariant. We can, for example, introduce
the change (6). Then the line element become :
(76)
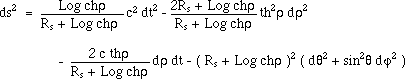
for r > 0
and :
(77)
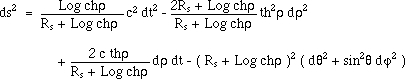
for r < 0.
"Radial" geodesics (For example q = p/2 , dj
= 0 ) focuss on the geometrical center O of the system (in this peculiar
representation). This point is comparable to an "hyperconic point".
A symmetry with respect to a point, in a 3d space, is a P-symmetry.
In this [ t , r , q , j ] the Schwarschild's line element is P-symmetric. It is also time-independent (invariant through time translation, i.e. corresponds to steady state) an T-symmetric, invariant through :
t ® - t