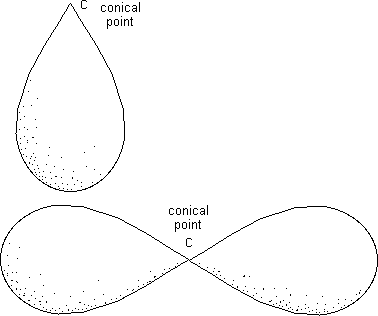
But surfaces do exist which are intrinsically singular, possessing singularities that are not due to a choice of coordinates. Here is an example: conic singularity.

Rough from the foundry, as formulated by Schwarzschild in 1917, the coordinates t , r , q , j (time, a radial distance and two angles, equivalent to azimuth and site : "spherical" coordinates) Schwarzschild's sphere is singular. For a certain value Rs of the "radial coordinate" r (supposed to be measured from a "geometric centre") this metric plays all sorts of games with us. One of the terms on the sphere has a non-nil denominator. In short, it is singular on this sphere. Is it an intrinsic singularity or an artefact introduced by a bad choice of coordinates ? That is the question we asked ourselves.
Let us note in passing the "Schwarzschild's geometry" is a four dimensional hypersurface, which makes the thing even more untrustworthy.
Kruskal focussed on this point. He constructed a coordinate change which, among other things, supplied a constant value for the speed of light along a radial trajectory. In doing so he concentrated the singular aspect "at the centre of the object" in a "central singularity". Psychologically we feel we have gained something. The solution becomes "regular almost everywhere", an expression that mathematicians use to say that a solution is regular, exempt of pathology, except on a unique point.
- You're not going to be difficult just over one little point surely....
Alas, Kruskal's formulation has a serious weakness : it does not give back the space of infinite special relativity. Technically it isn't infinitely lorentzian, "asymptomatically lorentzian".
It is an essential question in physics : do singularities exist . Does Nature tolerate singularity ? The answer is formulated in terms of belief (as for the existence or inexistence of infinity in fact).
We sought a new interpretation of this same Schwarzschild geometry by trying to eliminate all singularity and we managed to do so. Our answer is therefore :
- The singular character of the Schwarzschild solution is simply induced by a poor choice of coordinates.
Technically, everything rests on the change of variable :
r = Rs + Log chr
which is read : r equals Rs plus logarithm of the hyperbolic cosine of the variable r . Simple except for scientists, specialists or higher maths students. For those who are able to play with the formula, the value r can no longer become inferior to Rs, even when r takes any possible value from negative to positive infinity.
Consider a surface obtained by turning a parabola around a straight line, like this :
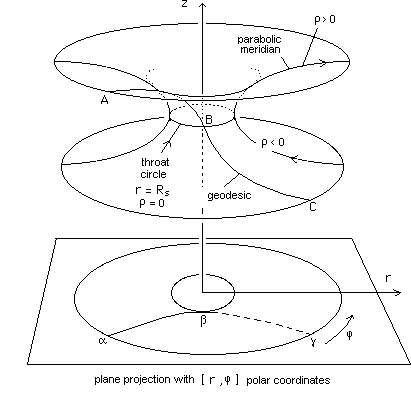
This figure was taken from the article. The surface is infinite, in fact, just like the parabola-meridian that created it by turning around the axis z shown. If we absolutely must represent it with its coordinates (r,z,j) we can expect trouble when we ask "what is this surface like when r < Rs ?"
An answer will be found ... imaginary, with roots of negative quantities. Simply because we are then "extra-surface".
This surface, in mathematics, is said to be "non-simply connected", a barbaric term which simply designates surfaces where any closed curve is unable to see its perimeter decrease, by sliding into the surface until it takes a value of zero.
This is possible on a sphere, which is "simply connected". But on the surface in question we can see quite clearly that a closed curve which "circles around the sort of central well" cannot see its perimeter tend towards zero, the limit being the perimeter of the "gorge circle". The same goes for a torus, which is also "non-simply connected".
We defined such a surface from its metric, which is a good illustration of our subject. When keeping the coordinate r, the surface seems to be singular. By using the change of variable given above, it is no longer so. What does the coordinate r correspond to ? It simply "runs" along the parabola's meridian as shown on the figure, taking the value zero on the circle of the gorge. Half the surface corresponds to r positive, the other to r negative. In the marking system of points [r , j ] there is no longer singularity.
We have decided to call this type of object a "toric bridge" by analogy with the torus.
However it is easily shown, still starting from metrics, that we can give an object a 3d hypersurface which has a "hypertoric bridge". Then there is no longer any gorge circle but a gorge sphere. The same goes for the surface above, a gorge circle seems to connect two 2d layers so that the gorge sphere connects two "3d half-spaces". If we are in one of these 3d half-spaces and we dive into the gorge sphere, we emerge in the other half-space.
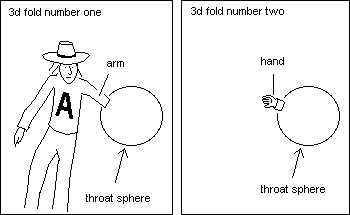
Let us return to the 2d surface shown above. The following figure shows how when we draw "circles that we believe to be concentric" we see their perimeter reduce, reach a minimum, then increase once more.
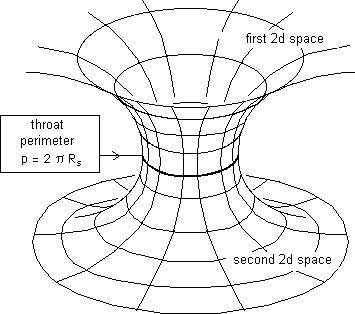
In 3d we have to imagine a sphere which completely englobes the gorge sphere Then another inside this (we should say "beyond" when following a given direction, towards the gorge sphere). We suppose that the surface of this sphere is less. However when we reach the gorge sphere, the surface passes through a minimum and then begins to increase ... to infinity if we continue the operation.
We have built "metrics" of the 2d and 3d surfaces which include a "toric passage" and a "hypertoric passage" and, in the second case, we have been struck by the resemblance with the Schwarzschild metric, where we undertook the change of coordinates and brought out its "non-simply connected" character, the "interior" of the object becoming simply "beyond the gorge sphere".
It was thus possible to eliminate all singularity.
At that stage we had simply extended the black hole model to a tandem of "black hole-white fountain". However, for the "exterior observer", the time required to cross the hypertoric bridge is still infinite. We seem to have simply improved the black hole model by explaining what it emerged as
We said earlier that the choice of variables, in a geometric solution is totally arbitrary. What goes for space also goes for time. We therefore sought a change of temporal variable as invented by Eddington in 1924 :
![]()
Once again, we only mention it for simple scientists and higher maths students.
t is the old "cosmic time", the ancient "chronological variable" presented in Schwarzschild's initial solution of 1917.
t' is the new "Eddington time". Rs is the "Schwarzschild radius (in which case we should say the Schwarzschild perimeter, divided by 2p ).
c is the speed of light (constant here).
Something which might seem odd : we mix time and space but, with matter, anything goes. The choice of time-marker is completely arbitrary. We ask only that :
- the metric be asymptomatically Lorentzian, that is to say that at infinity, space-time becomes Minkowski space-time, that of special relativity. In our case it works (not for Kruskal).
- the new time t' identifies itself, still to infinity, with the "time of a supposedly immobile observer". Which is also the case (not for Kruskal).
By doing so the time of free fall of a test-particle, infinitely immobile and falling towards the Schwarzschild sphere, becomes infinite in relation to "the time passed by the "exterior observer", who is far away and immobile.
However the particle would emerge from the swallowhole in an infinite time. As in the black hole we can enter into this sort of 3d swallowhole but can't come out, except in an infinite time.
The other side is a resurgence. But with such a choice of time (t') the particle emerges from the resurgence in an infinite time whereas it is able to penetrate in a finite time. That was a sticking point. The solution consists of effecting a sort of double change of variable, which we have the perfect right to do, for the bit of space-time that is supposed to be ours :
![]()
In the "twin universe" :
![]()
The cosmic mechanism thus functions perfectly.
- No singularity.
- We can enter the "swallowhole" but we cannot come out (black hole).
- We can come out of the resurgence but cannot go in (white fountain).
Good, you're saying, we're making progress...
Yes and no. The problem is that the transit time in the hypertoric passage is just a few hundredths of a second. And this Moloch is capable of swallowing anything, ten solar masses for example, in less time than it takes for a bullet to go through a playing card.
The conclusion is that through this more rational representation of the geometric solution, black holes could not exist. They are ... mathematical fiction. They can only exist by virtue of this "time freezing". However with "Eddington time", which satisfies all the demands of physics, transit time becomes finite.
Conclusion : this Schwarzschild geometry is, in our opinion, just a snapshot, an instant image, of an unstationary process of hyperspatial transfer. It is as if when shown a photo of an anvil someone had thrown in the air you concluded that all anvils float in air. The Schwarzschild solution is also the solution to an equation that implies that the universe is perfectly empty, that the density of energy matter is nil at every point. A bit like if someone showed you the photo of a football stadium taken after the players had left the field for half-time and you concluded that football was played on empty fields.
So what would happen ?
We have shown that during the passage through the gorge sphere, the time coordinate was inverted. If we call t' the (Eddington) time corresponding to our "side of space-time' and t'* the "time marker" of the twin universe we have :
t'* = - t'
Note that in 1967 Andrei Sakharov was the first to suggest that two universes with inverted times were created at the moment of the "Big Bang".
It remains to understand what is meant by "inversion of time". Does it mean that when we dive into the twin universe we become younger ? We have shown that this is not so. We "take our own time" and if we emerged a little further via a symmetrical structure, we would not be any younger than when we entered the twin universe. Impossible then to "kill one's own father" as in Barjavel's "Imprudent Traveller" ("Le Voyageur Imprudent").
Groups, once again, have allowed us to elucidate the "ontological" sense of the time coordinate inversion. When a particle plunges into the twin universe its gravitational action makes itself felt, but its contribution to the gravitational field then becomes negative. Its "gravific mass" inverses.
By the way, this totally justifies the model developed on the site and in the book "We have lost half the universe" ("On a perdu la moitié de l'univers") (Albin Michel). The masses that wander in twin universes behave as repulsive masses in relation to the masses present in our universe.
- According to Newton, Masses attract each other in our universe.
- According to Newton, masses attract each other in the twin universe.
- When masses situated in two "adjacent" portions of space-time interact, they repel each other.
This is a simple consequence of the inversion of the temporal variable (but not of time).
The groups also show how the duality matter-antimatter exists in both universes, as imagined by Andrei Sakharov.
When a particle of matter manages to pass into the twin universe (we'll see how later) it remains as matter, but "CPT symmetric". This is the meaning of the famous "CPT theorem" of physics (never proved. What Souriau calls a "physician's theorem"). Classically physicians say " the CPT symmetric of matter is identical to the matter". CPT symmetry means :
- The particle, in its new lair, moves in "backward time" : T-symmetry.
- It is enantiomorphic, inverted right and left, in "mirror" : P-symmetry.
- All its "charges" are inverted, including its electric charge, if it has one. This is C-symmetry.
For us, a particle's CPT symmetric is a particle of the twin (or that has entered the twin). It is a gemellary particle. As it has T-symmetry, its mass is automatically inverted (a result initially obtained by J. M. Souriau in 1974).
The C-symmetric of a particle is its antiparticle.
Feynman found that the PT-symmetric of particle behaved like an antiparticle. Exact, but it is question of ... the antimatter of the twin, with negative mass (because it also has T-symmetry). All that appears from the history of groups. This work makes the link between everything published up to now (on the site see Geometrical Physics B in the section 'geometrising antimatter'). A good illustration of this business of inversion of space can be obtained. In the paper we frequently insist on the idea of a representation space. It is the space in which we mentally represent geometric objects. Earlier we used an image in which Lanturlu thrusts his hand in the gorge sphere and it seems to emerge in another 3d universe. For the requirements of illustration the drawing is separated into two figures. But there is something that you probably didn't notice at first : Lanturlu puts his left hand in the sphere but it is his right hand that emerges. This is not an accident.
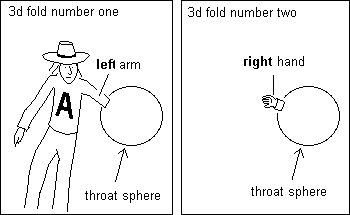
Where is the second universe ?
It is fitted into ours, which is a little difficult to understand. It will be simpler if we return to the 2d surface, the "flatland".
