Le physicien théoricien Lee Smolin vient de publier un ouvrage intitulé "Rien ne va plus en physique !" , aux éditions Dunod.

Lee Smolin

 

Un pavé de 485 pages. Mais j'en recommande la lecture. Je pense que cet ouvrage fera date dans l'histoire des sciences.

 

 

Je ne sais pas s'il existe un précédent de ce genre. Smolin est "au faîte de sa carrière", qu'il achève comme directeur de l'Institut Perimeter, au Canada. Ce livre retrace au passage sa carrière où il a participé pendant trois décennies à ce qu'on pourrait qualifier de recherche forcenée menée par des milliers de chercheurs pour tenter de donner un nouveau souffle à la physique théorique. Il signale par exemple qu'en trente ans des milliers de chercheurs ont publié quelques ... cent mille articles consacrés à la théorie des cordes, sans que ceci ne débouche sur quoi que ce soit de concret.

Avant de commenter cet ouvrage, je vous incité à suivre le dialogue entre Lee Smolin et Thibaud Damour, à la cité des sciences, organisé sous l'égide des éditions Dunod et de la revue Ciel et Espace, ce "débat" étant animé par le journaliste David Fosset, travaillant pour cette revue.

Celui qui n'a pas lu l'ouvrage de Smolin ne peut guère apprécier les répliques qui émaillent ce débat. Je voudai simplement faire quelques remarques. A un moment, Smolin dit que lorsqu'un progrès est enregistré dans les sciences, les choses se simplifient, deviennent plus claires, plus harmonieuses. Damour cite un exemple pour lui démontrer le contraire en évoquant un changement de vision pour le système solaire, par passage du modèle de Kepler à celui de Newton.

Le modèle de Kepler était purement phénoménologique. Il partait des observations très précises effectuées par l'astronome Danois Tycho Brahé. A partir de ces données il n'était plus possible, en considérant le modèle héliocentrique de Copernic de considérer que les trajectoires des planètes s'effectuaient selon des cercles. Vous vous souvenez sans doute des lois de Kepler.

- Les trajectoires des planètes sont des ellipses, le Soleil se situant à l'un des foyers.
- Les carrés des temps de révolution sont comme les cubes des grands axes.

Kepler avait constaté cela, mais ne " l'expliquait pas", il n'avait pas de modèle théorique pour justifier cela. C'est Newton qui permit de construire mathématiquement ces mêmes trajectoires en considérant simplement que les planètes étaent des "points-masses", attirées par le Soleil, autre point-masse, selon la loi à laquelle il laissa son nom. Il y a donc là une simplification. La constatation de Kepler peut alors se traduire par :

- Les trajectoires des planètes suivent les lois de la mécanique newtonienne, selon laquelle deux objets s'attirent proportionnellement à leurs masses et inversement proportionnellement à la distance qui les sépare.

Un mathématicien peut alors démontrer que ces trajectoires sont  planes, et sont plus précisément des côniques ( cercles, ellipses, paraboles ou hyperboles dans le cas d'astéroïdes ou de comêtes ).

Cet aspect donne donc raison à Smolin. Mais Kepler tenta en outre d'expliquer pourquoi les planètes s'étaient installées sur certaines orbites, et pas d'autres. Une démarche empirique débouche sur la "loi de Titus-Bode", qui ne connaissait pas à ce jour d'explication.
Kepler échoua dans une tentative de description de "nature géométrique", selon laquelle les trajectoires planétaires correspondaient à des "emboitements de polyèdres" ( voir ma bande dessin Cosmi Story, gratuitement téléchargeable sur le site http://www.savoir-sans-frontieres.com. plus précisément à ce lien. Il s'avéra que le modèle de Kepler ne cadrait simplement pas avec les observations.

Dans la vision de Newton, les planètes peuvent s'installer sur n'importe quelles orbites, la seule contrainte étant que leurs mouvements obéissent aux lois de la mécanique. Damour se sert de cela pour évoquer le fait que le modèle planétaire de Newton est " à paramètres libres ", ces paramètres étant les rayons des orbites. Il ne s'attache pas à la loi de Titus-Bode, parce qu'il ne voit pas son origine ontologique. L'essai de Kepler lui semble être une tentative de déterminer, sinon les valeurs des orbites, du moins leurs rapports. Ce discours évoque l'effort fait en physique théorique ( sans succès à ce jour ) pour essayer de comprendre ce que sont ces "paramètres provisoirement libres" que sont les masses des particules, et les rapports qui les lient entre elles.

Comme on le verra dans le livre de Smolin, la physique théorique contemporaine représente une explosion caricaturale du nombre de ces paramères libres, qui se comptent fréquemment par ... plusieurs centaines. Ce qu'on a jusqu'ici passablement dissimulé au public est le fait que, dans les approches les plus avancées de la théorie des cordes, les tenants de cette étrange discipline avouent que leur choix doit se faire entre 10⁵⁰⁰ théories possibles ( ... ), chaque théorie représentant un choix particulier de paramètres et de lois physiques. Bien sûr, on pourrait dire qu'il suffit de sélectionner dans ce "paysage théorique" la bonne loi, qui rendra compte des observations basées sur l'acquis incontestable de la physique des particules élémentaires. Malheureusement les partisans de cette théorie des cordes avouent n'avoir pas la moindre idée de la façon de procéder.

Mais revenons à cette évocation du passage d'un pseudo-modèle, celui de Kepler, concernant l'agencement des orbites, à un retour à la plus grande liberté, ces orbites devenant des paramètres libres.
En est-il réellement ainsi ?

Il existe un travail, dû au mathématicien Jean-Marie Souriau, qui montre qu'un système de masses orbitant autour d'un astre central, d'un soleil, distribue ses orbites selon un "loi dorée", par ailleurs très proche de la loi empirique de Titus-Bode.

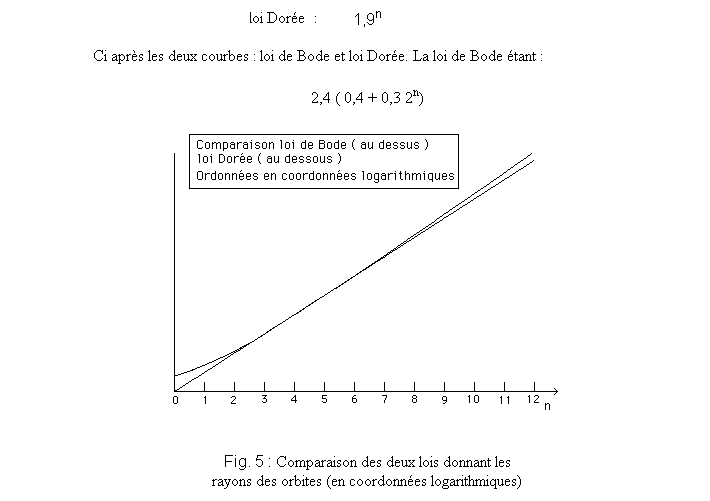
Je renvoie le lecteur au dossier présent sur mon site. En quelques mots, les planètes, en circulant autouur du soleil crée sur celui-ci un effet de marée. Prenons l'exemple du couple Terre-Lune. Assimilons le globe terrestre à une sphère parfaite, homogène. La lune va déformer la Terre en la transformant en un ellipsoïde dont le grand axe pointera vers le satellite. Il s'agit de marées terrestre ( un demi mètre ) et non de marées "marines". Chaque jour "lorsque la Lune passe au dessus de la Terre" la surface terrestre ( la croûte terrestre ) se soulève d'un demi-mètre.

Même phénomène lorsqu'une planète circule autour du Soleil. Elle transforme la "sphère solaire" ( ou "quasi-sphère" solaire ) en ellipsoïde, dont le grand axe pointe vers la planète en question.L'effet est en un sur r cube. Ainsi une planète comme Mercure parvient à créer, à la surface du soleil, le même effet que sa géante cousine Saturne, cet effet se traduisant par un soulèvement de quelques centimètres.

Les planètes "se servent ainsi du soleil" pour s'informer de leurs positions respectives. Le soleil leur sert de "résonateur", "d'antenne". Ces effets de marée conjugués font que le champ gravitationnel dû au soleil n'a plus une belle symétrie sphérique. Ceci se traduit par des altérations qui modifient les trajectoires des planètes.Le premier effet est de les amener à circuler toutes dans un même plan. Est-ce le plan perpendiculaire à l'axe de rotation ( initial ) du jeune soleil ?

Eh non. L'astre qui conduit le jeu, sur ce plan là est celui qui possède le "moment cinétique" le plus important, c'est à dire le MRV le plus important, où M est la masse de la planète, R le rayon de l'orbite et V la vitesse d'orbitation. Le soleil possède, lui aussi, un moment cinétique, qui se calcule par intégration. C'est la somme de tous  les mrv élémentaires. Toujours est-il que, de ce point de vue, l'astre dominant n'est pas le soleil, mais ... Jupiter, le "roi des dieux".

Une parenthèse. D'où viennent ces moments cinétiques ? Lorsque le système solaire se constitue le soleil appartient encore à un amas d'étoiles, collisionnel. Ca n'est que plus tard que cet amas se disloquera complètement, ce dont les astronomes n'ont réellement pris conscience qu'il y a à peine une dizaine d'années.

Avant que cet "amas lâche", dynamiquement instable,  ne se disloque, les proto-étoiles sont relativement serrées les uns contre les autres. Autour d'elles des systèmes planétaires se constituent. On pourrait plutôt parler de proto-systèmes planétaires.

Ces systèmes se frôlent, interagissent. Dans des livres j'ai comparé ces systèmes à des oeufs sur le plat se baladant à la surface d'une vaste poêle bien huilée. Les "blancs" frottent les uns sur les autres, pas les "jaunes". Si après les "oeufs sur le plat" se dispersent, on aura des "blancs" animés d'un mouvement de rotation, dotés d'un "moment cinétique", alors que le jaunes auront peu bénéficié de ces échanges d'énergie. Tout cela pour justifier le fait qu'une planète située à la périphérie du système solaire recèle l'essentiel du moment cinétique du système.

Les planètes vont dont modifier mutuellement leurs trajectoires par effets de marée, de même qu'elle modifieront l'axe de rotation du soleil. Dans les fait, la planète Jupiter va contraindre tout ce monde là à orbiter dans son plan de rotation, qui deviendra le plan de l'écliptique. On ne peut pas savoir comment était orienté initialement l'axe de rotation du soleil. Mais comme Jupiter a un moment cinétique supérieur au sien, c'est lui qui aura contraint cet axe de rotation à se redresser et à se situer dans une direction pratiquement perpendiculaire au plan de l'écliptique, au plan où circulait initialement Jupiter, devenu le plan de l'écliptique. Mais comme Jupiter possède un moment cinétique supérieur à celui du soleil, c'est lui qui aura contraint l'axe de rotation de celui-ci à se redresser et à se situer perpendiculairement au plan de son orbite.

Les effets de marée se traduisent par des modifications des orbites. Un de ces effets est leur circularisation. Souriau a mis en évidence le résultat de ces effets de marée sur les rapports des orbites.

Deux systèmes peuvent échanger de l'énergie par résonance. Prenez par exemple  un instrument de musique doté de deux cordes. La première a une fréquence de vibration N1 et la seconde une fréquence N2. Si vous pincez la première corde, la seconde ne restera pas indifférente aux ondes sonores qu'elle produira. Si les deux fréquences sont égales, l'effet sera maximal. Il subsistera si le rapport de ces fréquences est égal à un nombre rationnel, égal au rapport de deux entiers. Mais l'effet commencera à dégrigoler lorsque ce rapport tendra vers un ... nombre irrationnel, comme racine de 2.

Un mathématicien, Kantor, a alors construit une mesure du degré d'irrationalité d'un nombre donné. Au terme de cette étude on tombe sur une équation qui fournit "le plus irrationnel de tous les nombres" et c'est ... le nombre d'or :

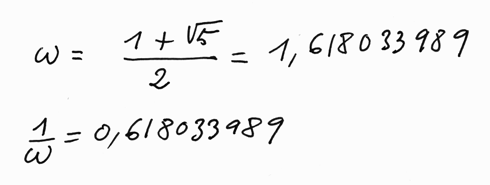
Au terme de son étude sur le degré d'irrationalité, Kantor trouve que le plus irrationnel de tous les nombres est solution de l'équation :

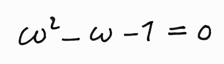
Revenons à un système planétaire avec un soleil et deux planètes. Au départ les orbites sont quelconques. Les trajectoires vont alors être modifiées par effet de marée, l'étoile centrale jouant e rôle d'antenne. Le système va évoluer jusqu'à ce que le rapport des périodes orbitales des deux planètes soit égal au nombre d'or. Le système aura alors convergé vers un état de résonance minimal.

S'il y a plus de deux planètes, le système est alors un peu plus complique, mais converge vers la "loi dorée" de Souriau. Il y aurait une jolie thèse de doctorat à faire avec tout cela, maintenant que la capacité de calcul des ordinateurs permet de gérer de tels systèmes. Ca ne serait du reste pas si compliqué que cela au sens où les planètes pourraient être assimilées à des points matériels. Seul le soleil devrait être "maillé" avec suffisamment de précision.

Damour se trompe donc quand il dit que le passage de Kepler à Newton a fait glisser l'astronomie vers un systèmes doté de nombreux paramètres libres. Ces trajectoires sont contraintes et tout ceci peut être déduit d'un mélange entre la loi de Newton est les équations de Navier-Stockes ( mécanique des fluides ), décrivant le comportement du soleil;

Peu de gens connaissent ce travail de Souriau, présenté lors d'un obscur congrès d'astronomie à Genêve en 1989, de plus en français ( Souriau n'écrit ni ne lit ou parle la langue de Shakeaspere, et à 85 ans passés il y a peu de chance que cela change ). Je ne pense pas qu'André Brahic connaisse ce travail. Ajoutons que le nombre d'or a mauvaise presse, dégage comme une odeur de soufre. Souriau serait-il porté sur l'alchimie ? Pas exactement, mais disons qu'il a beaucoup lu....

On retrouve le nombre d'or dans maintes constructions antiques. Même recherche de "non-résonance", mais cette fois vis-à-vis d'une résistance à la sismicité. Mais ceci, comme dirait Kipling, est une autre histoire. Revenons au débat Smolin-Damour. Les premier invoque Leibnitz, à la recherche des "causes premières". Immédiatement, Damour fait une réplique étonnante :

- Smolin est trop fin pour donner dans cette sorte de popérisme naïf (la phrase exacte est très proche ).

Karl Popper est un philosophe qui a mis en lumière le concept de "falsifabilité" d'une théorie. La traduction de ce mot prête à confusion. Falsifier, en français, signifie "faire un faux". Une traduction plus correcte serait "rechercher si une théorie peut être prise en défaut, prédire par exemple des effets qui ne seront pas observés". Pour Smolin cette démarche est incontournable. Pour Damour, s'agissant de la théorie des cordes, elle est simplement dépassée. Il invoque même un peu plus loin la célèbre expression italienne " si non e vero, esta bella " ( "si ça n'est pas vrai, au moins c'est beau" ).

En clair des scientifiques peuvent amplement justifier les trois décennies d'une carrière de physicien, même si cette démarche débouche sur le vide, à condition que "cela soit beau". Se rappeler à ce sujet le titre du livre de Michael Green " l'univers élégant" ( "he smart universe" ). Dans la théorie des cordes l'accent est mis sur "l'élégance". Mais comment se mesure-t-elle, selons quels critères doit-elle être appréciée ?

Je rappelle le bilan des travaux sur les cordes : cent mille papiers en trente ans.

Là, je laisse la parole au mathématicien Souriau. Selon lui ces mathématiques n'ont rien de très élégant. Les calculs sont d'ailleurs abominablement fastidieux. Smolin parle de millliers de lignes de calcul, comporant des izaines de termes, que les théoriciens doivent arranger sur d'immense cahiers, achetés dans les magasins de fournitures pour artistes (...).

Il semble bien que sa définition personnelle de la physique théorique se confirme :

Une physique sans expérience et une mathématique sans rigueur

Tout ceci est un premier commentaire sur ce livre de Smolin. Il me faudra y revenir. Quelques flashes en passant. Smolin situe l'origine de cette théorie des cordes, qui se situe d'ailleurs avant que n'apparaîssent le "modèle standard" ( les leptons, plus les hadrons, constitués de quarks ). L'idée sous-jacente est l'unification et elle est d'emblée fort séduisante. Ceci étant, je suis un peu comme tout un chacun. J'essaye de me faire une (vague) idée de ce que peut être cette fameuse théorie des cordes. On ne trouve pas d'ouvrages de vulgarisation ou de sensibilisation à cette approche. Smolin donne quelques repères.

Les physiciens connaissent le concept de Lagrangien ainsi que le principe de moindre action. On trouvera une introductions à ce concept dans " Les Aventures de Nicolas Boubakov " ( page 17 du pdf ), fruit d'une collaboration avec le mathématicien Boris Kolev, de Marseille. Boris a eu une excellente idée pour dégager le concept de Lagrangien, à partir du calcul ( exact ) de la forme du savon qui s'appuie sur deux cercles coaxiaux. Le film de savon s'établit alors de telle manière que son aire soit minimale. L'aire du film de savon se calcule à l'aide d'une intégrale. On peut calculer la forme de cette surface ( l'équation de la méridienne de cette surface de révolution ).

Boris se sert de ce point de départ pour étendre cela de manière beaucoup plus générale. L'aire du film de savon n'est alors qu'une "action" particulière, calculée grâce à une "intégrale", à partir d'une fonction, qui figure dans cette intégrale et qui n'est qu'un "Lagragien particulier". Pour un non-scientifique, qu'est-ce que cela veut dire ? Une "action" est une quantité qui se calcule selon "une intégrale", sur un "chemin". Ce chemin, assimilons-le au comportement d'un système physique dans une sorte d'espace de configuration. Il se trouve que de nombreuses solutions à des problèmes de physique peuvent se traduirent en terme de recherche d'une "action minimale". Le fait de "minimiser cette action" fournira le "chemin", la façon dont le système évoluera ou se comportera.

Un Lagrangien peut être tout simplement une fonction qui, intervenant dans une intégrale d'action permet de calculer la distance parcourue pour aller, sur une surface, d'un point A à un point B. Si on minimise cette distance, le chemin correspondra à ce qu'on appelle une géodésique. Il s'agit d'une image statique. Mais cette idée de géodésique, de "plus court chemin" a cours également dans l'espace-temps.

Pourquoi des "cordes" ? D'après ce que j'ai compris (...) une "corde" est censée, quand elle est ouverte, porter deux charges, une à chaque bout. Smolin évoque alors l'idée de champ électrique, matérialisé par des "lignes de champ" :

 

 

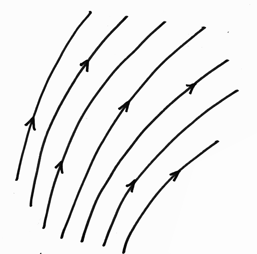
Lignes de champ électrique

 

On pourrait "recréer" ce champn en supposant que celui-ci se déploie dans le vide en disposant dans l'espace des objets qui soient les petites "cordes" à l'extrêmité desquelles se trouveraient des charges électriques, positives et négatives, comparable à des couples électron-positron.

 

 

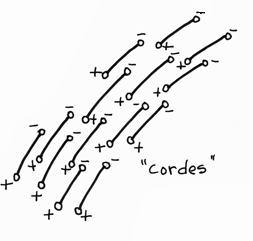
Une image qui suggère, très vaguement, que les cordes puissent représenter à la fois les "objets " et "les champs", les forces. L'idée sous-jacente est l'unification. .L'électrodynamique quantique représente ce genre de démarche " d'unification " où des élements conceptuels de la nature se trouvent inclus dans une même "famille", où on leur trouve " un air de famille ". Ainsi une particule chargée est un objet. Une force électromagbétique est ... une force. Au départ force et objets subissant l'action de ces forces, ou (/et) les créant semblent être des éléméments conceptuels de natures différentes. Dans l'électrodynamique quantique, quand deux particules chargées interagissent ( "agiussent mutuellement l'une sur l'autre" ) cette force procède par échange de particules qui vahicules la force, la "transportent" (d'où cette dénomination générique de "carriers" ). Les particules chargées interagissent par échange de photons virtuels. Ainsi la force et l'objet créant et subissant la force acquièrent des natures semblables. On réalise une unification. Comme noté par Smolin dans son livre dans son chapitre 4 : "L'unification devient science", ce thème de l'unification est au centre des préoccupations des physiciens contemporaines.

On verra par la suite que l'idée ( forte ) des gens de la "gravité à boucle, une de leurs idées, consiste à rechercher une description du monde où le contenant et le contenu sont " de même nature ", où "l'espace" et la "matière" seraient des "propriétés émergentes" d'une même structuren "prégéométrique".

La corde peut être à priori... tout. Elle évolue dans l'espace, elle vibre, peut se romprendre, se refermer sur elle-même. Tous ces contorsions sont censées représenter des phénomènes. Considérons une corde qui se déplace dans l'espace. Elle va épouser un éléments de surface :

 

 

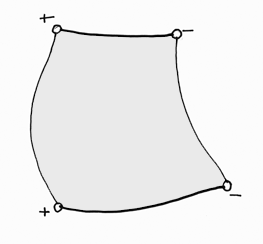
Surface envelope engendrée par le déplacement d'une corde porteuse de charges

 

Page 162 de son livre, Smolin énumère alors ce que la théorie des cordes, nouveau "leggo" de la physique théorique, est censé apporter. Il précise que "la liste est impressionnante" :

- La théorie des cordes nous fournit une unification automatique et "gratuite" de toutes les particules élémentaires; elle a aussi unifié les forces les unes avec les autres. Celles-ci proviennent de la vibration d'un objet fondamentale, la corde.

- La théorie des cordes fournit automatiquement les champs de jauge, qui sont responsables de l'électromagnétisme et des forces nucléaires. Celles-ci émergent naturellement des cordes ouvertes.

L'électromagnétisme est lié aux particules charges : proton, électron. Les forces nucléaires sont à l'oeuvre dans les atomes, lient les quarks, constituants des nucléons ( protons, neutrons ). Les phénomènes sont assimilés au comportement de cordes, à leur vibration indique une unification.

- La théorie des cordes nous fournit automatiquement les gravitons, qui proviennent des vibrations de cordes fermées. En conséquence nous avons obtenu gratuitement une unification automatique de la gravité avec les autres forces.

Effectivement. La force électromagnétique et les forces nucléaires, forte et faible, et la force de gravité dérivent du comportement d'un même objet : la corde.

Voilà donc ce que la théorie des cordes rend possible, conclut Smolin. On comprend que l'approche ait attiré les physiciens théoriciens comme une lampe attire les papillons de nuit. Imaginez qu'au début du siècle quelqu'un ait dit :

- Nous allons remplacer ce que nous avons jusqu'ici appelé particules par des ondes. Plus encore : nous allons unifier les ondes et les particules. Ainsi les objets que nous pensions être des particules sont aussi des ondes. A l'inverse les forces, liées aux ondes, seront à l'inverse identifiées à des .. particules, que nous appelerons " carriers " ( transporteurs ). Chaque force, chaque champ aura la sienne. La particule "transporteuse" associée à la force électromagnétique sera le photon. A la force nucléaire forte nous associerons des particules que nous appelerons gluons. Nous déciderons d'appeler ces particules transporteuses de forces des bosons. La force appelée interaction faible sera liée à d'autres types de bosons.

La tentation des cordes a dérivé de la même démarche "d'unification". La mécanique quantique représentait une unification ondes-particules. Là, ça a très bien marché. A terme ça a débouché sur ce qu'on a appelé le modèle standard, gérant les forces nucléaires, forte et faible et les forces électromagnétiques. Les nucléons, proton et neutron ont été "démontés" en quarks, liés par la force d'interaction forte, par "échanges de gluons". Tout cela s'est révélé compliqué mais prédictif. On a pu "casser des protons et des neutrons". Mais il s'est avéré que les forces liant les quarks croissaient avec la distance ( ou du moins est-ce ainsi qu'on a interprété l'impossibilité d'observer le comportement de quarks à l'état libre, qui auraient été identifiables, du fait qu'ils possèdent des charges électriques fractionnaires ). Ceux-ci ne pouvait cheminer à l'état libre et se recominaient immédiatement, pour donner d'autres particules, instables, etc..

Un joli jeu de construction, donnant ces "jets" que vous avez tous vus et qu représentent le résultat d'un "évènement", d'une collision qui se produit, à haute énergie, dans un accélérateur de particules. Très vite les théoriciens se sont dits " la force de gravité doit pouvoir "faire partie de la famille" : pour cela il suffit d'envisager l'existence d'une nouvelle particule "transportant cette force" : le graviton. Mais depuis un demi siècle, pas moyen de fabriquer un graviton décent, de "quantifier la gravitation". Or voilà que cette nouvelle approche basée sur un modèle qui semble très simples, avec un objet unique, la corde, ouverte ou fermée, semble promettre l'unification désirée. La force de gravité cesse d'être "exotique". Elle est simplement lié à la vibration de cordes fermées, comme l'a doctement rappelé l'académicien Thibaud Damour lors de la rencontre organisée à la Cité des Sciences de la Vilette, le face à face avec Lee Smolin.

Smolin ajoute un rapide coup de lampe, que nous pouvons attraper au passage. Lorsque la corde se déplace dans l'espace temps, elle épouse une surface-envelope, crée un objet bidimensionnel, une surface. Le dessin ci-après représente une interaction entre deux cordes fermées, qui fusionnent.

 

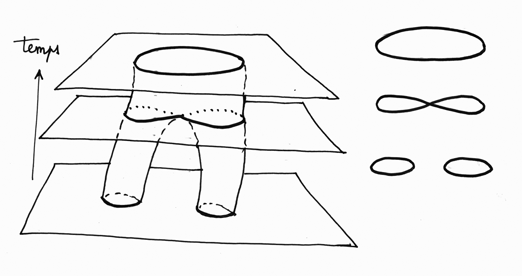
Les cordes envelopent une surface d'aire minimale

 

Smolin écrit, page 163 :

- Voilà donc le rêve que la théorie des cordes rend possible. Tout le modèle standard avec ses douze types de quarks et de leptons et ses trois forces, plus la gravitation, pourrait être unifié, tous ces phénomènes émergeant de vibrations de cordes qui s'étirent dans l'espace-temps suivant la loi la plus simple possible : que leur aire soit minimale. .... La théorie des cordes était si prometteuse qu'il n'est guère étonnant que Schwarz et ses collaborateurs, peu nombreux à l'époque, fussent convaincus de sa véracité. En ce qui concerne l'unification, aucune théorie n'a offert autant à parir d'une idée aussi simple.

Le fait que la surface soit minimale nous rappelle qu'en physique théorique beaucoup de choses se jouent en recherchant ces situations "extrémales".

Je ne vais pas réécrire ici le livre de Smolin. Toujours est-il que ce jeu ne pouvait pas se jouer dans u n bête espace temps avec trois dimensions d'espace et une dimension de temps. Apparaîssaient ce qu'il appelle des "anomalies", des aspects qui ne pouvaient pas permettre de cadrer avec la physique. Il était alors nécessaire d'introduire des dimensions supplémentaires, d'envisager que le jeu des phénomènes de la nature dusse se jouer dans un contexte géométrique plus riche, à dix dimensions, ce que Smolin décrit comme " neuf dimensions d'espace et un de temps". Ainsi les cordes " se déplaceraient dans un espace à neuf dimensions".

Et c'est là que les choses ont commencé à se compliquer dramatiquement. Ces dimensions supplémentaires, il faut les gérer. Or quand vous accroissez le nombre des dimensions d'espace, les choses se compliquent de manière ... "exponentielle". Partons d'un espace à une seule dimension. On ne peut envisager que deux objets : une courbe fermée et un segment terminé par deux points. Ajouter une dimension de plus. La famille des surfaces, des objets bidimensionnels devient tout de suite beaucoup plus riche. Les surfaces fermées contiennent la sphère, la ... surface de Boy ( voir " Le Topologicon" téléchargeable tratuitement ), le tore, la bouteille de Klein, plus une infinité de surfaces "ansées". Ajoutez les "surfaces à bord" : on ne s'en sort plus. Plus il y a de dimensions, plus ça devient compliqué.

Passons à la page 175.

- Un problème intéressant était posé. Peut-on choisir la géométrie des six dimensions supplémentaires de telle façon qu'en sorte exactement "le bon type de supersymétrie" ? Peut-on s'arranger pour que notre monde tridimensionnel ait une version de la physique des particules telle que décrite par les versions supersymétriques du modèle standard ? Philip Candelas, Gary Horowicz, Andrew Strominger et Edward Witten on montré que les conditions nécessaire pour que la théorie des cordes reproduise une version supersymétrique du modèle standard etait que les six dimensions supplémentaires constitue une structure géométrique explorée pour la première fois par les mathématiciens Eugenio Calabi et Shing-tung Yau. Cela réduisait l'abondance des possibilités.

Ce qu'on oublié de vous dire des gens comme Michael Greene dans son ouvrage l'univers élégant c'est qu'il existe au moins cent mille structures de Calabi-Yau différentes

 

Michael Greene, au moment de la parution de son livre " L'univers élégant "

Les revues de vulgarisation ont reproduit à l'envi l'aspect d'un de ces objet, ou d'un objet "parent", car il est impossible de dessiner une hypersurface à six dimensions. Vous trouvez ce dessin mystérieux dans l'ouvrage de Greene, que j'ai déjà commenté dans mon site.

 

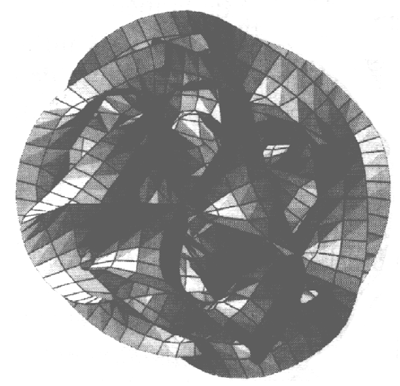
Et Smolin d'ajouter :

- Chacun de ces espaces produisait une version différente de la physique des particules. Chacun venait avec sa liste de constantes régissant sa taille et sa forme.

Smolin écrit dans son livre, page 359 : " j'ajouterai à mon réquisitoire...". Cette phrase figure dans un passage où il évoque la façon dont les théoriciens des supercordes mettent en doute "de manière particulièrement désagréable" les compétences professionnelles des gens qui ont choisi une voie différente. Et c'est bien d'un réquisitoire qu'il s'agit. Quand on assiste au face à face entre Smolin et Damour, le premier tient des propos beaucoup plus modérés que dans son ouvrage. Damour se présente avec une sorte d'assurance. Il évoque des "avancées" dont Smolin démontre dans son livre qu'elles sont simplement mensongères. A l'inverse Damour qualifie les essais de la "gravité en boucles", qui retiennent désormais l'attention de Smolin de " toy model " ( " modèle - jouet " ). Or Smolin est parfaitement clair dans ses pages. Il ne s'agit pas pour lui de revendiquer "les fantastiques succès et avancées de la gravité en boucles". Il la présente comme une autre approche et insiste en disant " En physique, nous avons globalement échoué. Il manque quelque chose, quelque chose de nouveau", idée qui ne semble pas effleurer une seule seconde Damour, très content de lui. Celui-ci illustre parfaitement cette suffisances des théoriciens des cordes que Smolin dénonce à longueur de pages;

Le Français Alain Connes, médaille Field a accepté de préfacer le livre. Citons un extrait de la page VI de sa préface :

- So, where is the trouble ? ( Alors, où est le problème ? ). Le problème, remarquablement analysé dans son livre par Lee Smolin, provient du déphasage de plus en plus perceptible entre les espoirs sans doute démesurées suscités par les premiers succès de la théorie ( des cordes ) sur le plan mathématique et leur portée réelle, malaise amplifié ( involontairement sans doute ) par une médiatisation sans retenue, articles de journaux, livres et programmes de télévision, présentant comme des vérités ce qui ne sont encore que des idées n'ayant reçu aucun a ssentiment de la nature.

Par "programmes de télévision", Connes fait allusion aux deux émissions de télévision montées par Brian Greene, sur les supercordes, parfaitement grotestes, du genre :

Si ma tante en avait, ça serait mon oncle

Ceux qui les ont vues ont dû avoir l'impression de se retrouver devant un clone des frères Bogdanoff, dans leurs plus mauvaises prestations. Ceci étant, ce jeune Greene s'est rendu mondialement célèbre. Son livre a été traduit dans toutes les langues et ses émission dans un grand nombre de pays. Or tout ceci, Smolin le montre à longueur de page, n'est que du vent, de la mousse. Il y a de quoi être totalement excédé.

Continuons avec cette préface de Connes :

- Que disent les ouvrages de vulgarisation et les articles de journaux ? Que la théorie des cordes rend compte non seulement du modèle standard, mais également de ses interactions avec la gravitation. Ayant travaillé longtemps sur ce modèle, j'ai voulu en avoir le coeur net et je me suis rendu au mois de juin 2006 à une conférence sur la théorie des cordes, à Cargèse. j'ai assisté aux discours des plus grands spécialistes du sujet et quelle ne fut pas ma stupéfaction de voir que même après avoir mijoté des dizaines de recettes de cuisine pour fabriquer la variété de Calabi-Yau adéquate, la réponse ressemblait très peu au modèle standard ( techniquement, par exemple, un doublet de Higgs par génération ). Il y a là un réel problème, car la science n'avance pas sans confrontation avec la réalité. Il est parfaitement normal de laisser du temps à une théorie en gestation pour se développer sans pression extérieure. Il n'est pas contre pas normal qu'une théorie ait acquis le monopole de la physique théorique sans jamais la moindre confrontation avec la nature et les résultats expérimentaux (...). Il n'est pas sain que ce monopole prive des jeunes chercheurs de la possibilité de choisir d'autres voies, et que certains leaders de la théorie des cordes soient à ce point asurés de la domination sociologique, qu'ils puissent dire : si une autre théorie réussit là où nous avons échoué, nous l'appelerons théorie des cordes.

 

Je ne peux qu'inciter mes lecteurs à lire le livre de Smolin avec attention. Il est édifiant. On trouve, si l'on veut, la clé de sa démarche à la page 363 de son ouvrage, où il écrit :

- En 2002, on m'avait demandé de présenter un panorama de tout le domaine de la gravité quantique dans un colloque organisé en l'honneur du professeur John Wheeler, un de ses fondateurs. J'ai décidé que la meilleure façon de brosser un tel panorama serait de faire la liste de tous les résultats importants mis au jour par les approches différentes. J'ai écrit un brouillon de ma liste, et naturellement un des résultats de cette liste etait la finitude de la théorie des supercordes.

Smolin n'indique pas ce qu'il entend exactement par cette finitude de la théorie. Je ne peux que hasarder une interprétation. Si un de mes lecteurs pense que je dis une ânerie, il me le signalera. En physique on exprime souvent des solutions d'équations sous la forme de développements en séries. Pour le lecteur non scientifique, qu'est-ce qu'un développement en série ? Prenons par exemple la fonction :

Y = sin ( X )

 

Elle peut être construite à l'aide d'une série comportant une infinité de termes, et qui est :

 

En mathématiques on note par un point d'exclamation ce qu'on appelle une "factorielle".

Ainsi "factorielle cinq" qui est 5 ! est égal à 5 x 4 x 3 x 2 x 1

On conçoit très bien comment cette série infinie de terme est construite. Le signe s'inverse, d'un terme au terme suivant. Les exposants sont impairs. Mais plaçons-nous maintenant dans la peau d'un physicien théoricien qui cherche la solution d'une certain équation, par exemple, et qui tombe sur la fonction, définie sous la forme d'une série :

 

Il devra se poser la question :

- Quand je me donne une valeur de X, est-ce que cette somme de terme correspond à une valeur finie ou infinie ?

En mathématiques on dira "est-ce que cette série converge ?"

Je ne sais pas à quelle finitude Smolin se réfère. C'est probablement beaucoup plus compliqué. En physique théorique beaucoup de choses se présentent sous la forme de séries et il est alors recommandé de savoir si ces sommes d'une infinité de termes donnnent des quantités finies ou infinies. Dans la cas de la série qui donne la fonction sinus, si on se contente des quelques premiers termes on obtient une valeur approchée très bonne de la valeur exacte, qui peut évidemment avoir une infinité de décimales. On appelle cela une valeur approchée. Quand on ajoute des termes supplémentaires on ne fait que de toucher à des décimales de plus en plus lointaines. En physique, il est fréquent qu'on construise une solution avec deux termes. Un "terme à l'ordre zéro" et un second terme représentant "une perturbation". J'ai moi-même construit une partie de ma thèse de doctorat en construisant une fonction selon une série de deux termes, qui me donnait la conductivité électrique d'un plasma. Est-ce que je me suis soucié de savoir si cette façon de construire cette solution à l'aide d'une série était valable ? Est-ce que cette série convergeait ?

J'avoue que je ne l'ai pas fait. Simplement parce que calculer le terme suivant aurait été affreusement compliqué. Je faisais de la "physique théorique", non de la "physique mathématique", nuance. Dans ce cas précis j'essayais d'apprécier la validité de mon calcul en comparant les valeurs numériques que je trouvais à des valeurs mesurées dans des expériences, et ça marchait assez bien. Mais ce genre de domaine qui s'appelle " la théorie cinétique des plasmas " on ne va en général pas plus loin. C'est ce que Smolin appelle du travail artisanal. On est face à un problème. Dans le cas dont je m'étais occupé il s'agissait de calculer la conductivité électrique d'un gaz ionisé avec deux températures, où la température électronique était sensiblement plus élevée que la température ionique. N'en déplaise à ce polytechnicien nommé Alain Riazuelo, j'ai été le premier à produire un modèle théorique qui donnait cela, qui permettait de calculer ces valeurs. J'ai publié cela dans plusieurs revues. J'en profite au passage pour évoquer un épisode qui illustre les failles du peer system, du système où les articles sont soumis à la critique d'un "referee", d'un "expert". En l'occurence j'avais envoyé ce travail au " Journal de Mécanique " ( devenu plus tard " The European Journal of Mechanics " ). L'accueil a été dramatique. J'ai failli louper mon entrée au Cnrs à cause de cela.rené germain, devenu par la suite secrétaire de l'Académie des Sciences de Paris, était directeur de cette revue. Il avait confié mon travail à un professeur nommé Cabannes ( probablement décédé, paix à son âme ). L'article, refusé, revint avec la mention :

- Ce travail révèle des méconnaissances profondes en théorie cinétique des gaz

J'étais mal, très mal. Le président de la commission qui devait se prononcer pour savoir si je serais ou non titularisé, intégré définitivement au Cnrs était .... Germain.

Durant les mois qui précédait la tenue de cette réunion, où les candidature ( au poste de chargé de recherche ) devaient être examinées je broyais du noir.J'étais un jour prostré dans mon bureau quand un groupe de Russes frappèrent à ma porte. Une interprète, taillée comme un capitaine de garde-côte, traduisait leurs propos comme une mitraillette.

- Monsieur Petit ?
- Oui
- Je vous présednte le professeur Luikov.
- Enchanté.
- Le professeur a tenu à faire un détour par Marseille pour vous rencontrer, parce que son collègue Vélikhov lui a beaucoup parlé de vous.
- J'en suis enchanté.
- Le professeur Luikov demande quel est votre dernier travail.

Je lui ai alors exposé ma théorie de la conductivité électreique des plasmas bitempératures. A l'issue de mon speech, l'interprête :

- Le professeur Luikov vous félicite. Vous avez résolu problème où lui et son équipe ont échoué pendant années. Il demande où ce travail est publié.

Un peu pris de court, je bredouille :

- Euh, je ne m'étais pas encore posé la question de savoir à quelle revue l'adresser.....

et l'interprête enchaîne :

- Nous serions très honoré de publier cela en Union Soviétique.

Je ne fais ni une ni deux et je lui tend le papier immédiatement. Deux mois après l'article sort dans la revue russe, traduit. Dès que je remettrai la main sur un tiré à part je scannerai la première page et ce mettrai cet imahe dans ce texte &&&. Un mois plus tard les éditions Américaines Pergamon Press m'envoient un courrier :

- Notre correspondant à Moscou a lu votre article. Nous demandons s'il nous serait possible de le publier dans une revue des Etats-Unis

J'accepte aussitôt ( mais là, j'avoue avoir oublié le nom de la dite revue ). Au printemps arrive la session de la commision du Cnrs qui devait décider si on me gardait dans la maison ou si on m'envoyait me faire voir ailleurs. J'avais déjà échoué plusieurs fois à cet examen d'entrée et, selon les statuts de la boutique, c'était ma dernière chance. J'avais pour appui un responsable syndical, qui voyait mon affaire bien mal engagée, jusqu'à ce que je lui passe les copies des deux articles

- Oh, chouette ! Là, je crois que je vais bien m'amuser.

La date de la session arrive. Germain, président, ouvre mon dossier avec emphase :

- Nous allons examiner maintenant le cas d'un chercheur que la plupart d'entre vous ne conaissent déjà que trop bien. Il s'agit de Jean-Pierre Petit.

Certains opinent du bonnet. D'autres lèvent les yeux au ciel. Germain parcourt mon dossier :

- Ce chercheur ne s'est pas entendu avec son directeur, le professeur Valensi, directeur de l'Institut de mécanique des Fluides de Marseille. On l'a donc affecté dans un autre laboratoire. Il a changé maintes fois de sujet de recherche. Il semble dispersé, brouillon. Certains émettent des doutes sur ses compétences.

Il sort un papier du dossier.

- Et là nous avons un avis du referee du Journal de Mécanique, que je dirige, qui nous dit que le travail qu'il a soumis, sur le calcul de la coductivité électrique d'un plasma révèle des méconnaissances profondes en théorie cinétique des gaz. Je propose donc que nous passions au vote. Qui est pour la titularisation de ce chercheur ? Qui est contre ?

Dans de tels moments on pourrait imaginer le grincement d'une guillotine.

Le représentant syndical intervient alors en distribuant à la volé des tirés à part de mon papier, en russe et anglais, comme on lance des cartes à jouer sur une table. Germain explore la version anglaise. Son visage se transforme aussitôt. Les "politiques" excellent aux changements de cap.

- Ah... eh bien je crois qu'il s'agit là d'une nouvelle information. Procédons au vote.

Et voilà comment je suis passé chargé de recherche, in extremis. Au passage le referee français, Cabanne, qui se présentait pourtant que le spécialiste français en matière de théorie cinétique des gaz passait pour un complet nul. Il faut dire que j'avais introduit une technique de calcul nouvelle "bi-paramétrique", qu'il n'avait pas comprise. Le papier a été, en outre, publié dans la revue français où il avait été refoulé. .

Fin de l'anecdote ( il y en a eu bien d'autres du même genre. La plupart des papiers que j'ai pu publier dans ma carrière sont ... tachés de sang ). Eh oui, je n'ai jamais su faire comme tout le monde, en rien. Toujours est-il que ce calcul était basé sur un développement en série, limité à deux termes. Comme je l'ai dit, il ne me serait pas venu à l'idée de montrer que cette série convergeait. C'eut été très compliqué. Vous découvrez ainsi un aspect de la physique théorique où la théorie est validée ... parce qu'elle marche à peu près, que cela rend des services. C'est de l'artisanat, pas de la rigueur mathématique, même si les outils utilisés ( ici des tenseurs ) sont parfois assez sophistiqués. .

En matière de théorie des supercordes les gens étaient obligés d'asseoir leur démarche sur des critères mathématiques, simplement parce qu'il ne savaient pas ... ce qu'ils calculaient au juste. Mais, s'ils présentaient par exemple des résultats sous forme d'une série de termes, la moindre de choses était de déterminer si oui ou non ce qu'il calculait était fini. Apparemment il existait donc un problème de finitude, jugé crucial, central par Smolin. Comme il est chargé de dresser un panorama de la théorie des cordes et de ses acquis il recherche les papiers ( sur les cent mille publiés en trente ans ) qui traitent de ce sujet. Il tombe alors sur le travail d'un nommé Mandelstam dont "tout le monde" considère qu'il démontre "la finitude de l'approche des cordes ". Il le fait lire par des mathématiciens, qui ne se montrent pas convaincus et lui répondent que ce travail est incomplet. Page 364 il écrit :

- J'ai commencé à poser la question aux théoriciens des cordes que je connaissais, en personne, ou par courrier électronique en leur demandant quel était le statut de la finitude et s'ils avaient la référence du papier qui en contenait la preuve. J'ai posé la question à une bonne dizaine de personnes, jeunes et plus âgées. Pratiquement tous ceux qui m'ont répondu ont affirmé que ce résultat était vrai. La plupart n'avaient pas de référence de la preuve, et ceux qui l'avaient m'ont dirigé vers le papier de Mandelstam. Je me suis donc tourné vers des articles de synthèse. La majorité disait explicitement que la théorie était finitaire. Soit ces articles se citaient les uns les autres, soit ils mentionnaient larticle initial de Mendelstam. Mais j'ai trouvé un article d'un physicien Russe qui disait que le résultat n'avait pas été démontré. J'avais du mal à croire qu'il puisse avoir raison alors que les gens qui étaient de l'avis contraire étaiuent tous des spécialistes éminents, que je connaissais parfois personnellement et pour qui j'avais la plus grande admiration.

Smolin, intrigué, commence alors une enquête pointilleuse pour essayer de tirer cela au clair. Il arrive à la conclusion que la chose est loin d'avoir été établie et rend compte de sa démarche, en écrivant, page 365 :

- Quand j'ai décrit cette situation dans ma présentation destinée au colloque en l'honneur de Wheeler, elle a été accueillie avec scepticisme. J'ai reçu des messages, pas tous gentils, qui disaient que j'avais tort, que la théorie était finie et que Mendelstam l'avait prouvé. La plupart des théoriciens des cordes étaient choqués quand je leur disais que la démonstration de la finitude n'avait jamais été menée jusqu'au bout. Personne ne se rappelait avoir entendu les théoriciens des cordes présenter ce problème comme une question ouverte. J'avais accepté de faire ce travail en raison de mon intérêt pour la théorie des cordes à laquelle à l'époque je consacrais tout mon temps. Néanmoins, certains théoriciens des cordes ont pris ma présentation comme un acte hostile.

Page 366, Smolin parle de cette question à son bon ami Carlo Rovelli ( du Centre de Physique théorique de Marseille ). Celui-ci lui répond qu'ayant reçu, lui aussi, beaucoup de messages lui affirmant que Mandelestram avait démontré la finitude de la théorie, il avait fini par contacter ce dernier. Smolin poursuit :

- Mandeltram est maintenant à la retraite, mais il lui répondit rapidement Il expliqua que tout ce qu'il avait prouvé était qu'une espèce particulière de terme infini n'apparaît nulle part dans la théorie. Mais il dit également qu'il n'avait pas en fait prouvé que la théorie était finie, car d'autres types de termes infinis pourraient surgir. Aucun des théoriciens des cordes avec qui j'avais discuté de ce problème, au moment où la démonstration finitaire de la théorie des cordes n'existait pas, n'a pris la décision d'arrêter son travail sur la théorie des cordes. Quand la question de la finitude sera résolue ( si elle l'est un jout ), nous devrons nous demander comment il est possible que tant de chercheurs n'aient pas été au courant du vrai statut d'un des résultats centraux de leur domaine de recherche, pourquoi beaucoup de théoriciens des cordes parlaient avec une telle aisance de leur domaine aux étrangers et aux nouveaux intiés en utilisant un langage impliquant que la théorie était parfaitement finitaire et cohérente. Et la finitude n'est pas le seul exemple d'une conjecture à laquelle tout le monde croît sans qu'elle soit démontrée.

A l'occasion de ce colloque de 2002, Lee Smolin, travaillant depuis près de trente années sur la théorie des cordes, en est amené à examiner les bases d'un édifice devenu déjà horriblement compliqué. Dès qu'ils inspecte une des bases de cette théorie, la finitude, il découvre que des milliers de chercheurs fonctionnent comme si cet aspect avait été parfaitement éclairci et démontré, alors que ça n'est pas le cas. Mais il était loin d'être au bout de ses surprises. Il se met à lire les écrits de splus grands spécialistes de la question y découvre des propos qui l'effarent. Une conjecture est une "proposition" émise par un mathématicien, et qui n'a pas fait l'objet d'une démonstration. Ce sont des choses courantes dans le domaine des mathématiques. Une conjecture est une propriété que l'on constate "dans de très nombreux cas" et pour laquelle on n'a pas trouvé de contre-exemple. Quand on a montré que la propriété était vraie dans tous les cas, alors la conjecture devient un théorème ( une proposition "vraie dans tous les cas" ). Mais ça n'est pas parce que cela marche "dans les très nombreux cas envisagés" que cette propriété est automatiquement vraie dans toute sa généralité.

Exemple de conjecture. Il y a pas mal d'années ( en &&& ? ) on a émis la conjeccture selon laquelle quatre couleusr étaient suffisantes pour colorier des pays sur une carte, sans que la même couleur se retrouve de part et d'autre d'une frontière. On a appelé cela " le théorème des quatre couleurs". En fait, tant que la démonstration ne fut pas établie ( en &&& ) il eut fallu parler de " la conjecture des quatre couleurs ". Puis cette démonstration apparut, fort longue, au terme d'une quête laborieuse et la conjecture devint théorème.

On trouve des conjectures dans de très nombreux domaines. Dans le domaine des cordesn Smolin en cite une, énoncée par Maldacena. En 2002 il tombe sur un texte écrit, entre autre, par une des sommités de la théorie des cordes, Gary Horowicz, et il lit :

- En résumé, nous voyons des raisons convaincantes pour mettre la conjecture de Maldacena dans la vatégie du vrai, mais non démontré.

Page 367 Smolin écrit :

- Je n'ai jamais entendu un mathématicien se référer à un résultat comme "vrai et non démontré". Par-dessus tout, ce qui est stupéfiant c'est que les auteurs, deux personnes fort intelligentes, ignorent la différence évidente entre les deux cas dont ils parlent. Au-delà, on ne sait si la théorie des cordes, ni si les théories supersymétriques de jauge existent réellement en tant que structures mathématiques. En effet leur existence même fait partie du problème. Ce que cette situation affirme clairement,c'est que les auteurs raisonnent comme si la théorie des cordes était une structure mathématique bien définie - malgré le large consensus proclamant que, même si c'était le cas, on n'aurait aucune idée de ce que serait cette structure. Concernant la défense de leur croyance en des conjectures non démontrées, les théoriciens des cordes notent souvent que queque chose est "de croyance générale" dans la communauté de la théorie des cordes ou "qu'aucunepersonne raisonnable ne doutera de sa vérité". Ils ont l'air de croire que l'appel au consensus à l'intérieur de leur communauté équivaut à un argument rationnel. ... ( page 371 ) Je comprends la difficulté à réfléchir clairement et indépendemment quand la recoinnaissance par la communauté demande une foi aveugle en un ensemble d'idées complexes dont vous le connaissez pas vous-mêmes les preuves. C'est un piège tel qu'il m'a fallu des années pour m'en échapper.

N'importe quel lecteur "doué de raison" restera sur le cul en lisant ces lignes. Elles conforment ce que dit Souriau depuis 30 ans à propos dela théorie des cordes, et de la physique thyéorique en général :

C'est devenu une physique sans expérience et une mathématique sans rigueur

Ce qui est nouveau est que c'est un transfuge de la communauté de la théorie des cordes, qui sait très exactement de quoi il parle, qui révèle ces faits. Le journaliste de Ciel et Espace, David Fosset, n'a visiblement pas perçu la gravité de cette situation, qui présente Smolin en début d'émission comme une sorte d'agitateur, à caractère marginal. Le débat a nécessairement une durée limitée. Smolin s'y montre très modéré, et même intimidé. Il est vrai que pour évoquer une telle question, cette de la non-démonstration de la finitude, les protagnistes risque que "larguer leurs auditeurs". Mais les débats scientifiques ne sont pas des conversation de coin de comptoir, ou des propos de salon.

Je me souviens de ce que m'avait dit un jour un journaliste de la revue Actuel :

- Dans les médias, ça n'est pas ce que tu dis qui porte, c'est ce que tu dégages.

J'avais lu l'ouvrage de Smolin avant de voir ce débat sur mon écran. J'ignore quelle a pu être l'impression du téléspectateur en voyant ces images et en captant ces propos.

 

 

J'aurais tendance à dire que ce face à face laissera peu de traces dans l'esprit du public. Et peut être en sera-t-il de même pour le livre de Smolin. Damour a publié en 2002 aux Editions Odile Jacob avec Jean-Claude Carrière un ouvrage intitulé :

Entretiens sur la multitude du monde
et l'unicité des idées

J'avais fait une note de lecture à l'époque à laquelle on accèdera en cliquant sur le lien. Pour moi ce livre est ... vide. Mais bon. Si un type comme moi le dit, ça ne porte pas. Il a fallu qu'un homme comme Lee Smolin se mette à parler pour que cela prenne une toute autre épaisseur.

J'ai beaucoup annoté l'ouvrage de Smolin, comme à mon habitude. Ce que je peux faire c'est extraire des phrases de son livre en citant les pages. J'ose espérer que cela éclairera un peu le lecteur.