Come trasformare una superficie Cross Cap

in una superficie di Boy (destra o sinistra, a scelta)

passando per la superficie romana di Steiner.

Italiano : Andrea Sambusetti, università di Roma

27 settembre - 25 ottobre 2003

pagina 4

Presentiamo il modello ancora da un altro punto di vista :

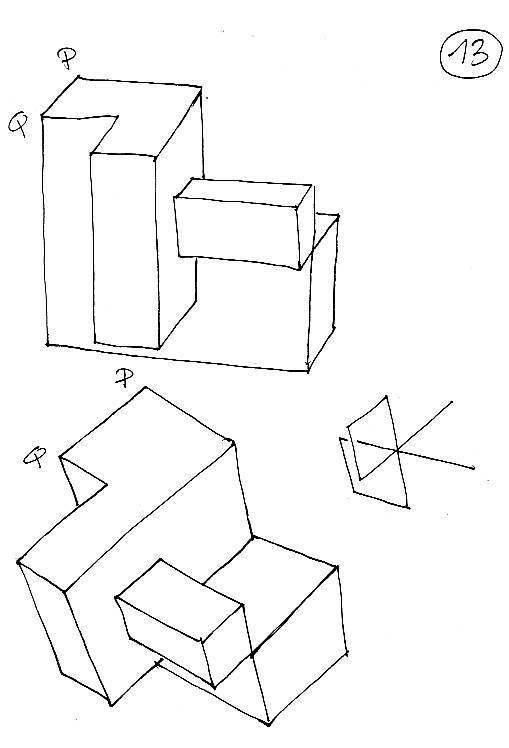
Tavola 14 : ripetiamo sempre la stessa operazione creando il terzo "orecchio" della curva di autointersezione. Nel modello poliedrico, quest'ultima ha la forma di tre quadrati con un vertice in comune : il punto triplo T .

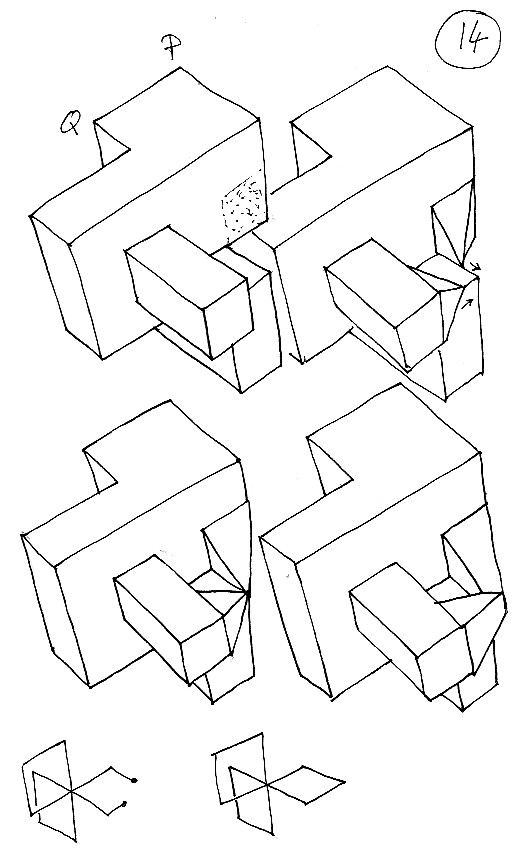
Tavola 15 : ruotando l'oggetto ritroverete la versione poliedrica della superficie di Boy che avevo presentato nel Topologicon (dove potete trovare anche un piano di montaggio che permette di costruirla).

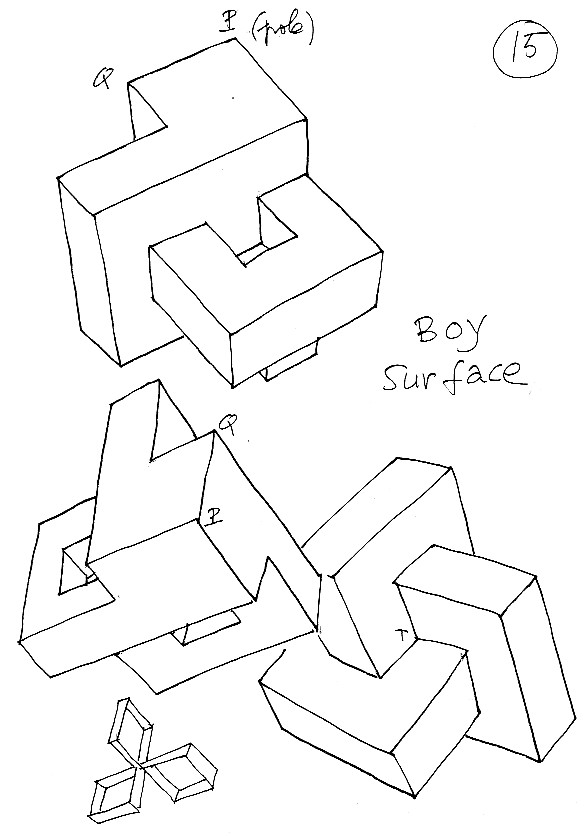
Ultima tavola : ho cercato di illustrare la superficie di Steiner mentre si contorce e si trasforma in superficie di Boy.

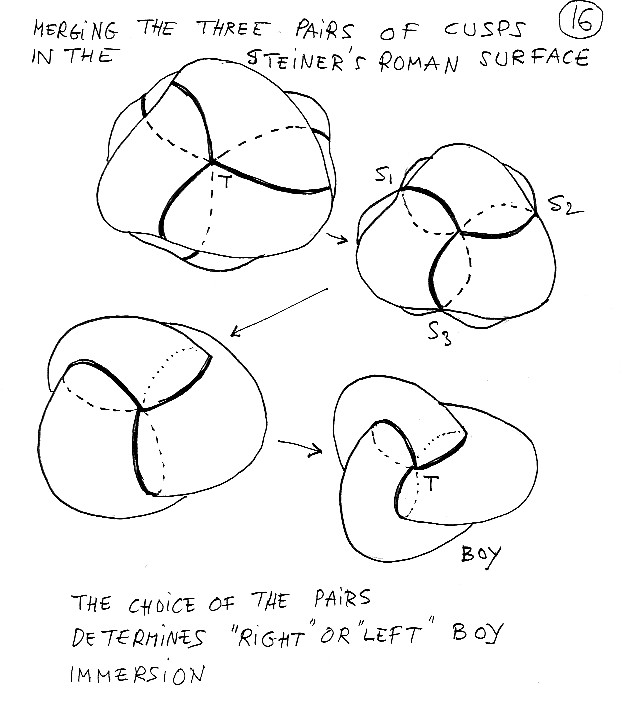
Vediamo che, disegnata in "rotondetto", ci vuole un bel po' di pratica per capirla. Il nostro occhio è molto a disagio quando si tratta di comprendere un oggetto per il quale, su una stessa linea visuale, si sovrappongono più di due falde. Da qui l'interesse del modello poliedrico, che mette alla portata di chiunque, se solo se si tenta di costruire da soli i modellini, delle trasformazioni considerate complicate in geometria. Notiamo per inciso che, a seconda delle coppie di punti cuspidali scelte, si ottiene un superficie di Boy "destra" o "sinistra" (definizioni completamente arbitrarie). Il piano proiettivo si immerge nello spazio tramite due rappresentazioni "antiautomorfe" speculari. Vediamo quindi anche che si può passare da una superficie di Boy destra ad una superficie di Boy sinistra attraverso un modello "centrale" che è la superficie romana di Steiner.

Sarebbe senza dubbio carino se questi disegni fossero pubblicati in riviste come Pour la Science o La Recherche. Ma da vent'anni mi è “proibita” la pubblicazione su queste riviste a causa di deviazionismo ufologico. Grazie, signori Hervé This e Philippe Boulanger. Ho perso il conto degli articoli di questo genere che ho proposto a queste riviste e che mi sono state gentilmente rifiutate. Si finisce coll'abituarsi al proprio statuto di scomunicato.

A titolo aneddotico, esiste un "premio d'Alembert" destinato a ricompensare gli autori di libri di divulgazione matematica. La storia mi è stata raccontata da un membro della commissione incaricata di decidere a chi doveva essere attribuito il premio (ci sono comunque questioni di soldi dietro). Dialogo :

- Insomma, perché non diamo il premio a Petit? Ha scritto delle opere notevoli come il "Géométricon", il "Trou Noir" ed il "Topologicon".

- Sì, ma non ha fatto solo quello.

- A cosa alludete?

- Ha anche scritto il "Mur du Silence".

- Ah, beh, allora....

Ebbene sì, il "Mur du Silence", pubblicato nell'1983, è un album dedicato alla MHD. E, come ognuno di noi sa, questa scienza corrosiva ha come pregio, o difetto,  di consentire ai dischi volanti di muoversi a velocità supersonica senza fare Bang.

« Cachez cette science, que je ne saurais voir »

Ho nelle mie scatole una versione magnifica del "rovesciamento del cubo", che non è la versione poliedrica della variante di Morin. Tutta farina del mio sacco. Uno di questi giorni....

22 ottobre 2003 : Non ci si affanna troppo su queste pagine, se devo credere al contatore. Lunedì 13 ottobre 2003 ho fatto un seminario al CMI (Centro di Matematica ed Informatica di Château-Gombert-Marseille) su invito di Trotman. In quell'occasione ho potuto tirar fuori una collezione di una trentina di modelli in cartone, di cui un giorno potrete gustare la primizia, poiché sono stati fotografati da Christophe Tardy.

Quando si dà un seminario, si crea una certa atmosfera. Nella foto qui sotto, ecco un geometra che esprime la sua perplessità.

Sullo sfondo, una parte dei modellini esposti con l'aiuto del mio collaboratore di lunga data, Boris Kolev, membro del dipartimento, anche lui geometra. Ad un certo momento ho posto la domanda :

- Quanti di voi hanno già visto una superficie romana di Steiner? Alzate la mano.

Nessuno l'aveva mai vista. Mi è sembrato quindi utile presentare quest'oggetto, con un programma di realtà virtuale, sul portatile che avevo con me, programma realizzato con l'aiuto di Christophe Tardy, ingegnere, e di Frédéric Descamp, dell'Istituto Laue Langevin di Grenoble (ILL). Palesemente questa presentazione sconcerta il pubblico, poco abituato a vedere le superfici matematiche fare giravolte a piacere.

Due tavole di cartone, visibili in primo piano, hanno permesso di presentare tutta la successione di modellini nel loro ordine logico. I modelli in verde e giallo illustrano, in forma poliedrica, lo strumento essenziale di creazione-scioglimento di una coppia di punti cuspidali. L'oggetto bianco più distante è una versione poliedrica della superficie Cross Cap, che si trasforma prima in versione poliedrica della superficie romana di Steiner, quindi, un metro più in là, a piacere, in superficie di Boy "destra" o "sinistra".

L'analisi dei modellini fa emergere varie osservazioni nel pubblico. Uno dei geometri domanda :

- Se è vero che, seguendo i modellini in quest'ordine, si può passare dalla superficie Cross Cap a quella di Boy, sembra che, seguendo il procedimento opposto, si possa trasformare una superficie di Boy in una Cross Cap.

Rispondo affermativamente. Imbaldanzito, il mio interlocutore aggiunge :

- Allora, se arrivati allo stadio superficie romana di Steiner ci si ferma, dovrebbe essere possibile ritornare ad una superficie di Boy, ma riflessa rispetto a quella iniziale.

Acconsento una seconda volta. Ma, purtroppo, nessuno si proporrà per dare qualche chiarimento su questo strano mondo in cui si permette alle immersioni delle superfici chiuse di avere dei punti cuspidali, creati o sciolti a coppie, il cui insieme costituisce una specie di estensione del mondo delle immersioni. Il termine "summersione" mi sembra conveniente. Se un lettore è capace di dare qualche chiarimento, è il benvenuto.

 

Curvatura concentrata in un punto cuspidale.

La calcoleremo sommando gli angoli al vertice e paragonando questa somma al risultato che si ottiene nel caso del piano euclideo : 2 p .

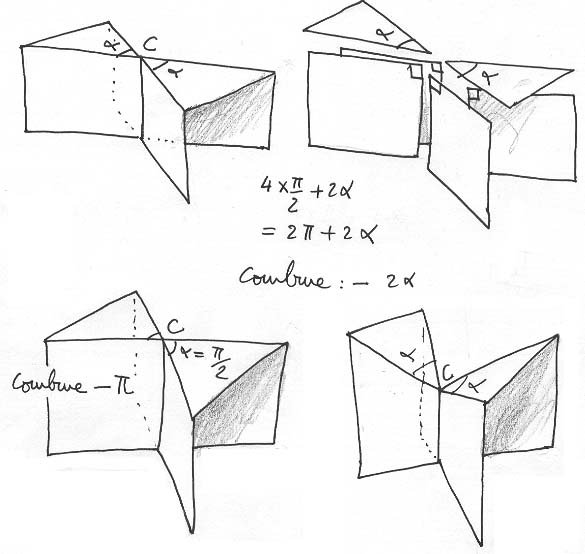
In alto a sinistra potete vedere una delle molte possibili rapresentazioni poliedriche di un punto cuspidale. "Smontando" la superficie si giunge ad una somma di angoli che supera il valore 2p di 2a . Se ne deduce che la curvatura angolare concentrata intorno a questo punto C è - 2a. Se l'angolo a è uguale a p/2 allora la curvatura negativa vale -p (figura in basso a sinistra). In effetti, a curvatura di un punto cuspidale può assumere infiniti valori. In basso a destra accentuiamo la somma angolare e la curvatura diventa allora < -p (abbiamo aumentato la curvatura negativa).

Operando in modo inverso, possiamo giungere ad una situazione abbastanza sorprendente: possiamo fare in modo che la curvatura (angolare) concentrata in C sia ... nulla :

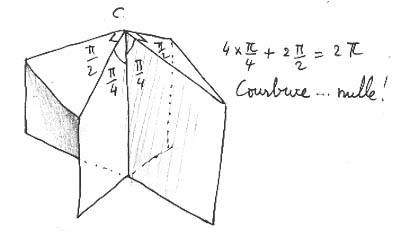
Partiamo ora da una rappresentazione poliedrica della superficie Cross Cap in cui figurano due punti cuspidali ognuno dei quali di curvatura uguale a -p :

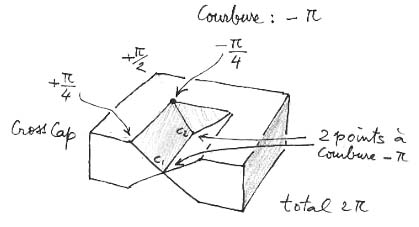
In questa figura ci sono otto "posiconi" corrispondenti di valore + p/2. Aggiungiamo quattro altri "posiconi" di curvatura + p/4 e quattro "negaconi" di curvatura - p/4.

Più i due punti cuspidali di curvatura - p .

Totale : 2 p

Dividendo il valore di questa "curvatura totale" per 2p ritroviamo il valore della caratteristica di Eulero-Poincaré di qualsiasi rappresentazione del piano proiettivo (o della superficie di Boy).

Nel corso della conferenza ho evocato l'arte e il modo di permutare i due punti cuspidali di una superficie Cross Cap utilizzando il rovesciamento della sfera. Non so più se ho messo questa cosa da qualche parte sul mio sito. E' un tale garbuglio. Bisognerà che cerchi, sennò lo aggiungerò. E' divertente. Fatto sta che questa operazione non piacque affatto ad una delle persone presenti al seminario:

- Non vedo perché Petit faccia uso di tanto armamentario per dimostrare la simmetria che unisce i due punti cuspidali di una Cross Cap. Si può fare molto più semplicemente.

E fece alla lavagna il disegno di una sfera schiacciata tra due righelli che si toccano e che dà effettivamente un insieme di autointersezione sotto forma di un segmento ai cui estremi si trovano due punti cuspidali, come la superficie Cross Cap. Sfortunatamente, e il signore i questione se ne accorse, questa non è la superficie Cross Cap.

- Diavolo, ma che cos'è allora? Domandò qualcuno.

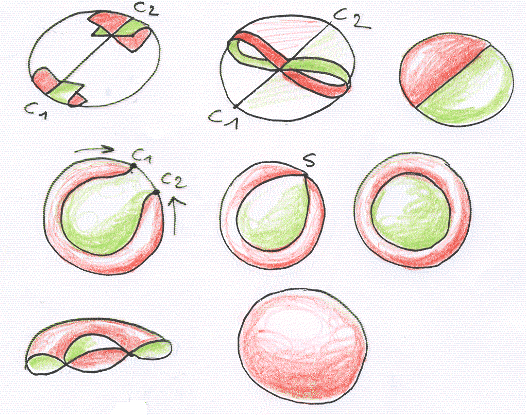
E' semplicemente l'immersione di una sfera, con due punti cuspidali. Se li si fa confluire verso un unico punto si ottiene una linea di autointersezione che diventa un cerchio. E si ottiene (in basso a destra) un'immersione della sfera che ci resta solo da trasformare nel suo embedding standard. Possiamo anche dare una rappresentazione poliedrica di questa superficie : 

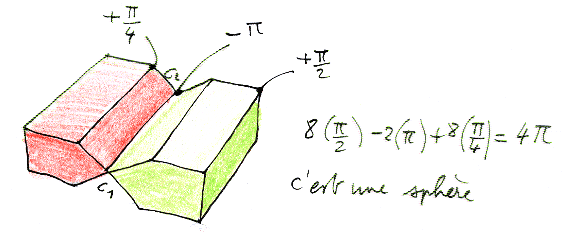
Si tratta di una superficie bilatera la cui curvatura totale è 2p.

Insomma, ci di può divertire parecchio con queste "summersioni". Consideriamo un'immersione di un toro ottenuta facendo girare il simbolo di "infinito" attorno ad un asse :

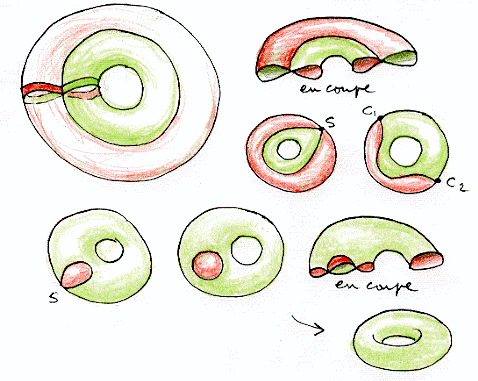
La tecnica del fare confluire dei punti cuspidali in un unico punto ci permette di arrivare rapidamente all'embedding standard del toro, come spiegato sopra nei disegni in successione.

Ma le cose non risultano sempre così facili ed evidenti. Prendiamo per esempio una sfera schiacciata tra due segmenti che, questa volta, sono più corti del diametro. Otteniamo ancora due punti cuspidali.

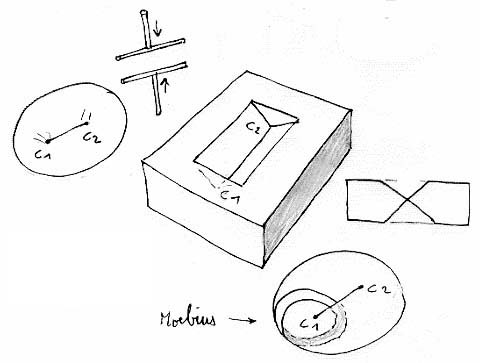
Poiché questa superficie contiene un nastro di Moebius, è unilatera. Abbiamo messo accanto una sua rappresentazione poliedrica che consente di calcolarne la curvatura totale. Troviamo allora zero. Se non mi sbaglio, dovrebbe allora essere una bottiglia di Klein. Di essa generalmente si conosce solo l'immersione classica, in cui la linea di autointersezione è un semplice cerchio. Ma ce ne sono altre, come questa qui. Confesso che non ho ancora trovato il modo di trasformarla in un'usuale bottiglia di Klein. D'altra parte, non so neppure se questa "immersione" e quella classica stiano nella stessa classe di omotopia (per la sfera, per esempio, ce n'e' una sola).A priori, non è detto: il toro infatti può essere immerso in quattro modi differenti nello spazio tridimensionale, che non possono essere trasformati l'uno nell'altro tramite un'omotopia regolare. In attesa di scoprire se sia possibile o meno in questo caso, mi sono divertito a trasformarla creando due punti cuspidali in più, ottenendo così due Cross Cap collegate da un tubo. Scomponendole, si ritrova che la caratteristica di Eulero-Poincaré fa zero.

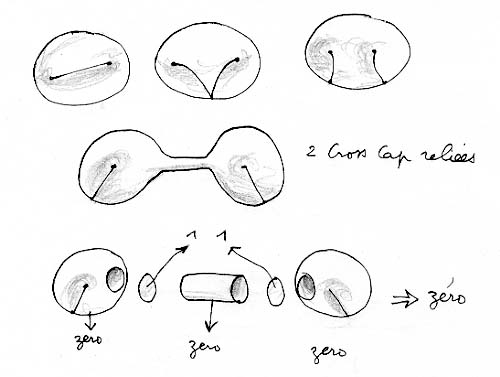
Questa strana superficie dovrebbe trasformarsi in una delle 4 possibili immersioni della bottiglia di Klein, ma quale? In ogni caso, eccone qui una ottenuta facendo ruotare un 8 attorno ad un asse, mentre lui stesso esegue nel frattempo un mezzo giro su se stesso :

Pagina precedente

Torna all'indice "Trasformazione di una Cross Cap in Boy "

Torna alla sezione Novità            Torna alla sezione Guida           Torna alla Pagina Principale

Numero di visite dal  25 nov 2004 :