8 - Didactic image for twin universe concept.

...Personally, I am deeply convinced that our vision of the Universe will drastically change within the next decades. Things go too bad in theoretical physics. Superstring theory looks like a nightmare for physicists. Some, like Misho Kaky, say that "it corresponds to a distant physics, far beyond our today's possibilities". I think that it corresponds to nothing, in spite I admit that a better understanding of the universe will imply an extension of the number of dimensions. As I tried to show, it could imply some sophistication of the geometrical vision of the cosmos. But, if I confess my deep opinion, we are just playing with very primitive tools. Our today's physics, with respect to the "next physics", to be completely invented, could be as different as classical mechanics can be from relativistic or quantum mechanics. Is space time a continuum ? We cannot answer this question. Many years ago, some scientists, like Werner Heinsenberg, suggested that space could be quantified. Let us explore this idea. When we play checkers we move the draughts on black squares, so that we don't use the white ones.

Fig.39a : Normal checkers' board.

Another party could be played on such white squares. Following, two distinct parties played on the same chechers' board :

Fig.39b : Two parties played on the same board.

Next, a portion of space. At the center, a small cluster of matter (white draughts), located on black suares.

Fig.39c : A cluster of particles, in a quanticized space.

...Conversely, we can imagine un small cluster of twin matter, which occupies black squares :

Fig.39d : A cluster of particles, in a quanticized space.

...For people who could have some difficulty to imagine what a twin universe could look like. Next, un small cluster of matter, surrounded by an homogeneous distribution of twin matter :

Fig.39e : A didactic image of quanticized twin universes.

...Unoccupied squares figure some "no-matter's land". Notice that an inhabitant of "one universe" would see only what's shown on figure 39c. A curvature effect would suggest two sets of draughts ("normal" and "twin") interacting only through gravitation :

Fig.39f : The white draught "feels" the presence of the grey "queen", which belongs to the other game
due to the deformation of an elastic board. .

...Following, a 3d game field :

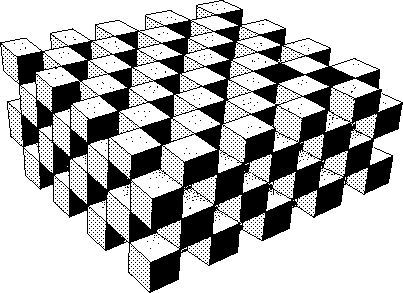
Fig.39g : Quanticized 3d space.

9 - For theoretical physicists only : why herperspace transfer reverses the mass.

....The reader must be familiar to the concept of moment, as developed by the mathematician J.M.Souriau in reference [15]. For detailed presentation, see my website : "dynamic groups in physics".

....The Lorentz groupe is axiomaticvally defined by :

where G is the followin "mirror matrix" :

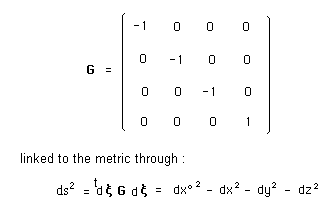
....The x vector is nothing but the space-time vector :

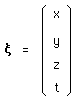
....The Lorentz group own four components. Two are "orthochron" and two "antichron" (after J.M.Souriau). The best way to understand this classification is to look at the four following matrixes, contained by these four components :

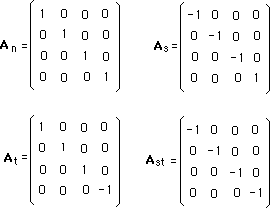
....A_n keeps space and time unchanged and belongs to the neutral component of the group (in fact, it is the neutral element of the group.

....A_s reverses space (P-symmetry).

....A_t reverses time (T-symmetry).

....A_st reverses space and time (PT-symmetry).

....A_n belongs to a subset of matrixes : A_n

....A_s belongs to a subset of matrixes : A_s

....A_t belongs to a subset of matrixes : A_t

....A_st belongs to a subset of matrixes : A_st

Following Souriau, we write :

A_o = A_n U A_s

U means "union" (of the two sets of matrixes). A_o represents the orthonchron set, which is also a subgroup of the Lorentz group, whil it contains its neutral element A_n.

A_a = A_t U A_st

....A_a is the antichron subset (which is not a subgroup).

....From the Lorentz group we may form the Poincaré group, which rules the movement of the relativistic mass-point :

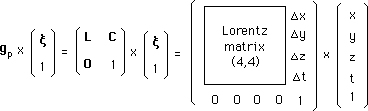
here represented with its action on space-time x .

....C is the space-time translation vector :

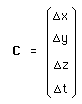
....As the Lorentz group, the Poincaré's group four components. We may define the following elements of the Poincaré's group, built with adequate Lorentz group elements.

g_p ( L_n , C)

g_p ( L_s , C)

g_p ( L_t , C)

g_p ( L_st , C)

...Souriau writes the ten component momentum of the Poincaré's group :

J_p = { J1 , J2 , J3 , J4 , J5 , J6 , J7 , J8 , J9 , J10 }

J_p = { E , px , py , pz , fx ,fy , fz , fx ,fy , fz } = { E , p , f , l }

...The Poincaré's group runs the movements of the relativistic mass point. E is the energy, p the impulsion, f the "passage" and l the "proper spin" (after Souriau). Souriau defines the 4-vector :

...Then he expresses the moment in a matrix form :

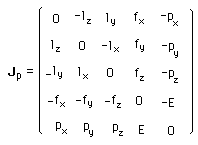
and shows that the coadjoint action of the Poincaré's group on its moment space can written :

..f depends on the chosen system of coordinates. A suitable choice can be give f = 0 , so that the matrix moment reduces to :

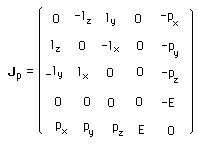
..Souriau has shown, in 1972 (geometric quanticization) that the l vector what quanticized and identified to the spin vector. That was the firts geometric definition of the spin.For example they are two momentum matrixes, corresponding to z-motions of photons, with two distinct helicities :

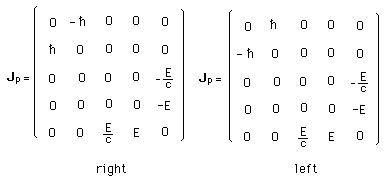
..Two momentum matrixes corresponding to neutrinos following z-motions :

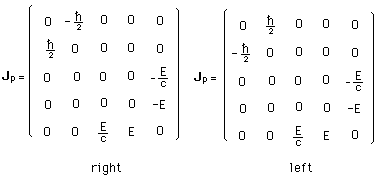
..The momentum for non-zero mass particles is :

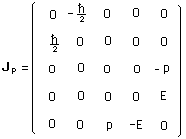
where :

..