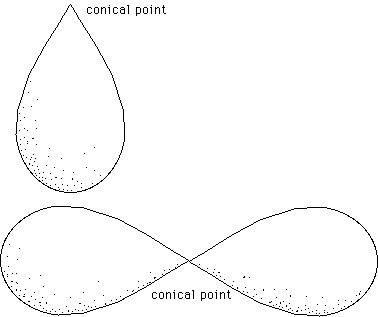
Oppositely, real intrinsic singularities exist, on surfaces. They are true geometric singularities :
(55)

(56)

(57)

And so on...

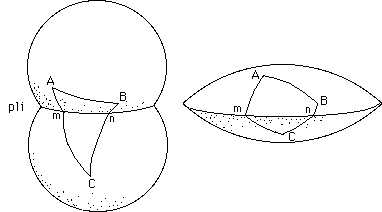
By the way a fold is a peculiar region of a surface where linear curvature is concentrated. On figure (57), left, we have a negative linear curvature. On the right a positive linear curvature.

We used in each sub-figure two portions of a sphere. The global object has the same topology as the sphere, which means that its total angular curvature is 4p .

Suppose the object on the left was built with two portions of spheres containing, each, a 3p angular curvature.

This is too much. Then the (negative) linear curvature must balance that, in order to give the final required value 4p :

 
As a conclusion our fold contains a negative curvature :

This curvature is uniformly distributed along the circular curve, along the fold.

Return back to figures (57). We have figured triangles, built with geodesic lines. But the way you can cross a fold without any problem with a (narrow) sticky-tape. You know how to compute, to predict the sum of the three angles of the triangle. You just need to compare the area of the triangle to the area of the sphere. The excess of curvature is :
(58)

But you have to take account of the (negative or positive) curvature contained in the portion of the fold, in the arc mn. It is :
(59)

Suppose a sort of lens, on the right of figure (57) is built from two portions of a sphere, each containing a p angular curvature. Therefore, if we forget the fold, this set of two portions of a sphere contains a 2p angular curvature. But this lens has a spheroidal topology. The angular curvature contribution must be 2p. Then :

You can also predict the sum of this strange triangle, formed from three geodesic lines. The arc mn contains the linear angular curvature :
(60)

When measuring the amount of angular curvature contained in the fold, inside the triangle, one can size the depart from the euclidean sum, which is p .

You see that you can handle these curvature problems, on surfaces, relatively easily.

A surface may own conical points, or fold lines. They are intrinsic singularities, not these artificial singularities, due to some choice of coordinates. Notice we can smooth the fold. Then we get a peanut :
(61)

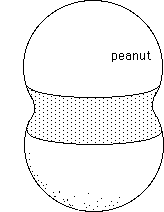
This is similar to smoothing the point-like summit of a cone (concentrated angular curvature), transforming the object into a blunt cone (angular curvature displayed on a portion of a sphere).

Suppose the two portions of sphere, above,on figure (61) represent 2/3 of a sphere, each, i.e a curvature
(62)

The grey portion of the "peanut" contains negative curvature. Precisely :

(63)