a703

The J.M.Souriau's work about the solar system. (p:2)

The theoretical prediction fits well the observational datas, except for the resonant couple Neptun-Pluto, as expected.

What about the Titus-Bode law ?

From the above theretical result Souriau builds immediatly a "golden law" :
(a710)

1,9ⁿ

Next, the golden law and the Titus-Bode law are compared, the latter corresponding to :

2,4 ( 0,4 + 0,3 2ⁿ)

(a711)

Fig. 5 : Comparizon of the laws giving

the orbital distance in logarithmic values.

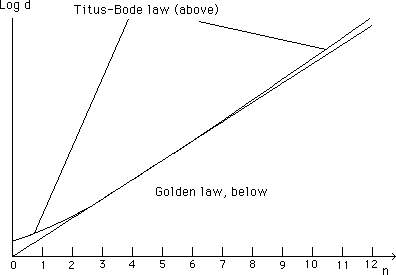
If we consider its rotation period, the Sun follows this law. The interpretation is the follwing: Souriau supposes that all the system is shaped by dissipative processes, due to tidal effects.

Then he applies his method to the satellites of Saturn :
(a712)

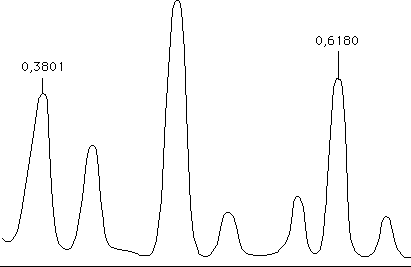
Fig. 6 : Fourier transform analysis for

orbitation periods of Saturn' satellites.

The two typical peaks apper again. Selecting these two lines, Souriau builds the reciprocal Fourier transforms. The result is given on figure 7. Notice that the Sun "behaves like a satellite of Saturn".
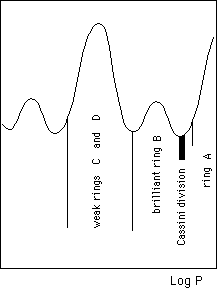
(a713)

Fig.7 : Expected values of the orbitation periods P of the satellites of Saturn, derived from a spectrum limited to the two lines w et w²

By the way the rings of Saturn fit very well the golden law.
(a714)

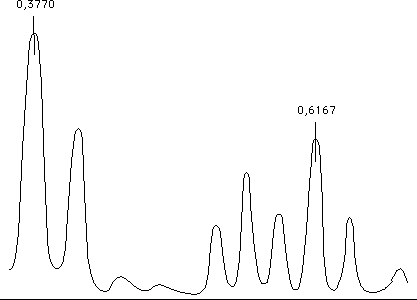
Fig.8 : Expected values of the period P of Saturn' rings, based on a reciprocal Fourier transform limited

to the two lines w and w²

Similar results, for the set of Jupiter' satellites.
(a715)

Fig.9 : Fourier transform based on the measured orbitation periods values.

Fig.10 : Expected values of the orbitation periods P of Jupiter' satellites, calculated from a reciprocal Fourier transform based on the two lines w and w²

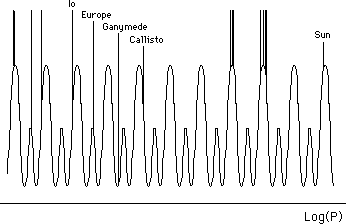
Notice the presence of the Sun, considered as "a satellite of Jupiter".