...This work was presented by J.M.Souriau in 1989, in a scientific meeting devoted to gravitation, held in Genova, Swizerland. The title of the paper was :
...Souriau starts
from the analysis of the orbital periods of the different planets. The Earth
turns around the Sun in 365 days. The duration of the Venusian year is 225
days. From these two numbers Souriau builds a Fibonacci series (where any
term in the sum of the two precedent ). We know that the ratio of successive
terms tends to the golden number. He compares the values to the orbitation
periods.
30 Sun (29 days)
55 nothing
85 Mercury (88
days)
140 nothing
225 Venus
365 Earth.
590 (1 year and 7 months):
Mars (1 year and 10 monthes)
955 nothing
1545 (4 year and 3 months):
Ceres-Pallas ( belt of asteroids)
2500 nothing
4045 (11 years):
Jupiter (11 years and 10 months)
6545 nothing
10590 (29 years):
Saturn ( 29 years and 5 months)
17135 nothing
27725 (76 years)
Uranus (84 years)
44860 nothing
72585 (199 years)
Neptun (165 years), Pluto (248 years)
...Then he studies
resonances in couples of planets. Mathematicians (Liouville, Hurwitz, Borel)
have build a mathematical test, a "measure of the level of irrationality of
a given number", how "far" it departs from a rational fraction, from the ratio
of to integers.
(a701)
Borel introduces the number :
q(x) if the lower limit, when q takes rational values.
q tends to be zero if x is close to a rational number. We get a curve showing the measure of irrationality q(x) of a given number x. Among all possible values, two numbers are the most irrational ones
- The he golden number :
(a702)
- and its square : w2
= 1 - w = 0,3820...
as can be seen on the following diagram .
(a703)
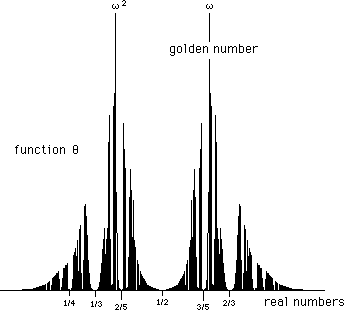
This function q(x), which has nothing to do with any observational material, is a pure mathematical object. The visible gaps corresponds to rational fractions ( q = 0 ).
Next : the orbitation times, where the unit is the Earth's
year.
Mercury : 0,2408425
Venus : 0,6151866
Earth : 1,0000000
Mars : 1,8808155
Ceres-Pallas : 4,604
Jupiter : 11,86178
Saturn : 29,45665
Uranus : 84,0189
Neptun : 164,765
Pluto : 247,68
Compute the ratio of the orbitation periods of Neptun
and Pluto.
(a704)
...If one calculates the ratio of two successive periods, one sees that these ratios lie between 1/3 and 2/3. Five ratios lie between 0.35 and 0.40. The couple Neptun-Pluto is a resonant one.
Souriau applies the test evoked above to couples of planets.
Neptun-Pluto : x = 2/3 x 0,9980 q = 0,01
Uranus-Neptun : x = 1/2 x 1,0199 q = 0,04
Uranus Pluto : x = 1/3 x 1,0176 q = 0,05
Venus-Mars : x = 1/3 x 0,9812 q = 0,06
Jupiter-Saturn : x = 2/5 x 1,0067 q = 0,07
...We see that two distant
planets, Neptun and Pluto, own exceptionally strong resonance. Souriau decides
to neglect this peculiar couple of planets, in the following analysis, based
of Fourier analysis of the periods Pj:
(a705)
On next figure IF(a)I4
is plotted.
(a706)
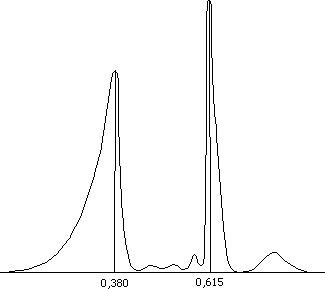
...Souriau finds two significant
peaks for values 0,615 and 0,380 , fitting very well with q(x)
curve of figure 1. See figure 3. :
(a707)
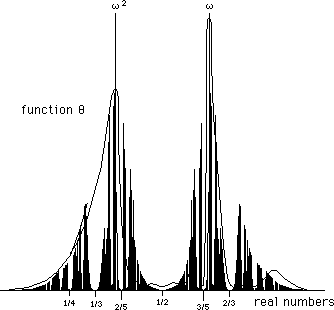
...He concludes that, as
a whole, the solar system is a non-resonant, or a weakly resonant system.
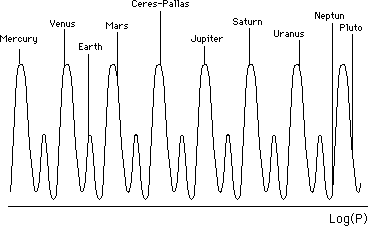
He makes an inverse Fourier transform (reciprocal) in order to build the probable
values of the orbital periods. The reciprocal Fourier transform
(a708)
can be built from selected lines ak. He selects the two
peculiar lines :
Then he gets the following results. The true values of
the orbital periods are indicated.
(a709)
![]()