Starting from the work of reference [3] we modify the model, in order to avoid encounters between positive and negative mass particles. The solution is to build a two-ten-dimensional folds (F,F*) as the quotient of the group by its orthochron sub-group.

Then we get two spaces with opposite arrows of time.

We study the impact of the different components of the group on momentum and movement spaces. One shows that the duality matter-antimatter occurs in boths folds, in both universes. This work gives a new insight on antimatter, through geometrical tools.For an example Dirac's antimatter is the antimatter of our own fold. The matter of the second fold is CPT-symmetrical with respect to ours.The PT-symmetrical of a matter particle that belongs to our fold is the antimatter of the other fold. Matter and antimatter particles of our universe own positive mass and energie.Matter and antimatter particles of the second fold own negative mass and energy.

1) Introduction.

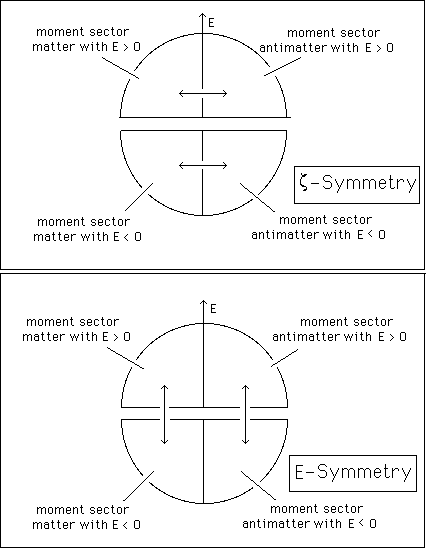
In a former paper [1] we have introduced a geometrical definition of antimatter, through a z-symmetry. Charged mass-points are supposed to move in a ten-dimensional space, with two sectors :

By the way, photons follows the { z ⁱ = 0 } surface.

It looks like Plato's cavern. The play is supposed to take place in a ten dimensional theater and, inside a four dimensional cavern called space time we observe 4d shadows, 4d movements.

In [1] we introduce a group which is an extension of the orthochron part of the Poincaré group. It makes possible to describe the charges of the particles in terms of additional components of their moment . In the paper [2] the group is duplicated, through a z-symmetry, which gives a geometric description of Dirac's antimatter. This last owns positive mass and energy.

Next step, paper [3], we decide to include antichron elements in the group. Then we get symmetries including T-symmetry, i.e. PT-symmetry and CPT-symmetry. We find that the PT-symmetrical of a particle of matter is an antiparticle, as suggested by Feynmann. We find that the CPT-symmetric of a particle of matter is a particle of matter too, as asserted by the so-called "CPT-theorem". But, from the coadjoint action of the group on the momentum components we find that these two own negative masses and energies. Then it is no longer possible, as suggested by Feynmann, to identify the PT-symmetry and the C-symmetry. Similarly the CPT-symmetry is different from identity, for it reverses the mass. As pointed out in [3] a solution, suggested by the mathematician J.M.Souriau [4] is to give up the antichron part of the Lorentz and Poincaré dynamical groups. But PT and CPT symmetries dissapear.

In the following we suggest another solution.

2) Building a group acting on a two folds space.

From [3] the action of our 16-dimensions group on a tend-dimensional space corresponds to :

(1) (4501)

 
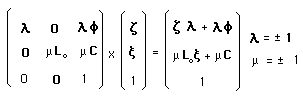
and the corresponding coadjoint action is :

(2) (4502)

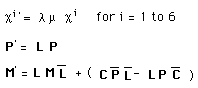
See computational details in the annex.

 
We build the two-folds space as the quotient of the group by its orhochron sub-group. From (1) a point of space is defined by :

(3)

 
Introduce a fold indix f = ± 1

The a point M of the first fold, called F, is defined by :

(4)

 
and the conjugated poit M*, which belongs to the second fold F*, by :

(5)

 
We can write the new action :

(6) (4506)

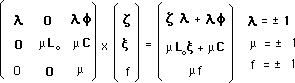
The coadjoint action on the momentum space is unchanged. But the interpretation of the results is different. Negative energy movements occurs in another fold. Positive and negative energy particles cannot meet, for the move in distinct ten-dimensional twin spaces.