f4403

Geometrization of matter and antimatter through coadjoint action of a group on its momentum space. 3 : Geometrical description of Dirac's antimatter. A first geometrical interpretation of antimatter

after Feynmann and so-called CPT-theorem. (p3)

...

Two more sectors has to be explored. On the third we examine the impact of (

= - 1 ;

= - 1 ) element on the momentum and movement.

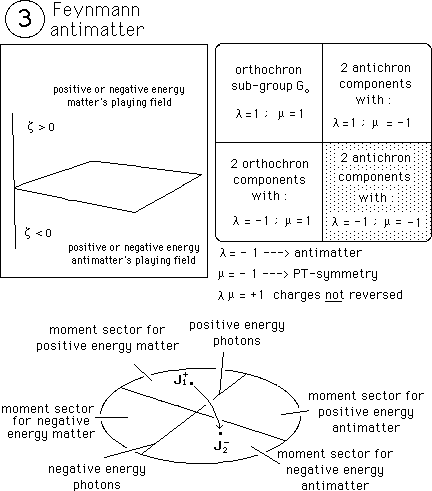
...( l = - 1 ) reverses the {zⁱ}. According to our geometric definition this new movement corresponds to antimatter, for it takes place in the second sector of space { z¹, z² , z³ , z ⁴ , z ⁵ , z ⁶, x, y , z , t }.

( m = - 1 ) gives a PT-symmetry, reverses the signs of ( x, y , z , t )

...But ( l m = + 1 ) keeps the charges unchanged. This is "PT-symmetric antimatter", so that it is a geometric description of antimatter after Feynmann.

...But the group belongs to the antichron sector, so that (coadjoint action) the energy and the mass of the particle is reversed.

...PT-symmetrical object does not identify completely with Dirac's antimatter, for it changes the sign of the mass. If such particles exist, they can produce full annihilation with positive mass particles.

Fig. 6 : ( l= -1 ; m = -1 ) elements transform movement of normal matter into movement of antimatter (z-Symmetry) of PT-symmetrical object, runing bacward in time.

Geometric description of Feynmann's vision of antimatter.

Does not identify vompletely with Dirac's one : negative mass and negative energy.

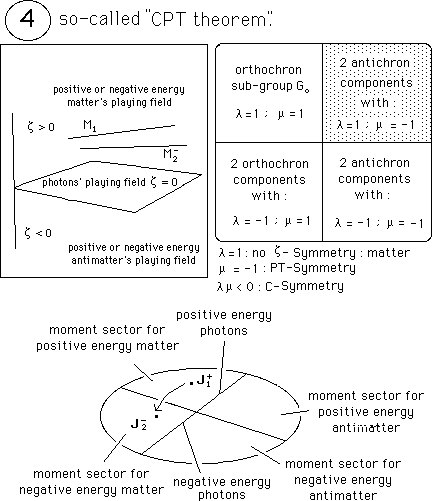
The last elements correspond to the sector ( l= 1 ; m = -1 )

( l = 1 ) --- > the movement is still in the matter's sector :

no z-Symmetry.

( m = -1 ) goes with a PT-symmetry. The particule runs backward in time.

( l = -1 ) : C-Symmetry. The charges are reversed.

...This is CPT-symmetrical matter, so that it corresponds to a geometrical interpretation of the so-called "CPT theorem", which asserts that the CPT-symmetric of a particle should be identical to that particle. That's not true. This movement corresponds to an antichron movement. The particle goes backward in time, si that (caodjoint action) its mass and energy become negative .

If CPT-symmetrical particle do exist and if they collide normal particle, complete annihilation occurs.

Fig.7 : ( l = 1 ; m = - 1 ) case. Corresponds to CPT-symmetry.

But the coadjoint action gives negative mass and energy.

The CPT-symmetric of a particle of matter is a particule of matter, but with negative mass.

...

Now, examine the impact on photons movement and moment. The

Symmetry has no impact on it : there is no "antiphoton". As all the charges of the photon are zero a does not change it. It is identical to its antiparticle.

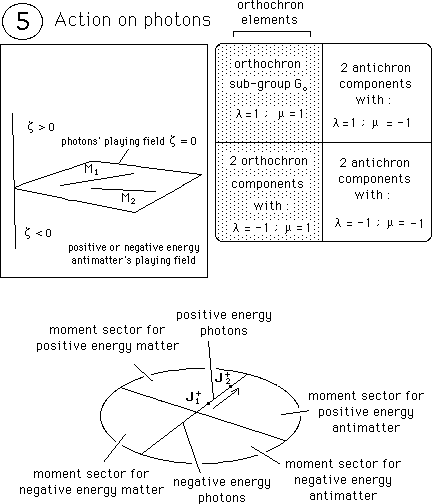
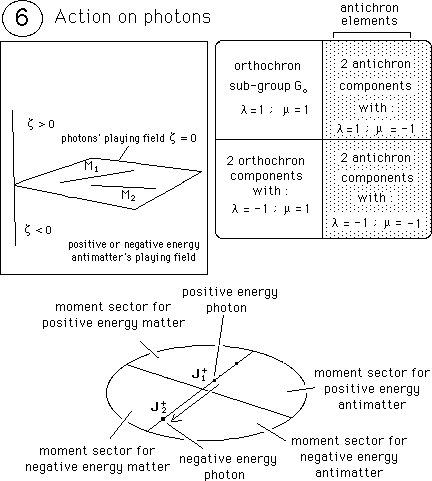
...The coadjoint action of orthochron components modifies the movement and the moment of the photon, but keep unchanged its energy. See figure 8.

Fig. 8 : Coadjoint action of orthochron elements

on photon's movement and moment.

Fig.9 : The coadjoint action of antichron elements on photon's movement and moment,

reverses the photon energy : it travels backwards in time.