...Through a new four components non-connex group, acting on a ten dimensional space, composed by (x,y,z,t) plus six additional dimensions we give a description of particles like photon, proton, neutron, electrons, neutrinos ( e, m and t ) and their anti, through the coadjoint action on the momentum space. Quantum numbers become components of the moments. Matter and antimatter are interpreted as two different movements of mass-points in this

 
matter movement taking place in the {z ⁱ > 0} half space and antimatter in the remnant {z ⁱ < 0} one.

The z-Symmetry :

which there goes with charge conjugation, becomes the definition of matter-antimatter duality.

1) Introduction.

...As pointed out by J.M.Souriau in his book [1] the Poincaré group, as a dynamic group for physics, arises a problem about the sign of the mass.

Everything starts from the Lorentz group L, whose element L is axiomaticaly defined by :

(1)

where :

(2)

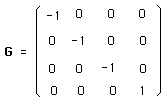
The Lorentz group acts on space-time :
(3)

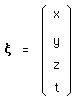
through the action :

(4)

 
The matrix G comes from the expression of the Lorentz metric (with c=1) :

(5)

We know than the Lorentz group is composed by four components :

L_n is the neutral componant, which contains the neutral element 1, i.e. the peculiar matrix :

(6)

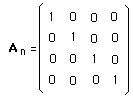
L_s , the second component, contains the matrix :

(7)

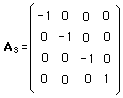
which reverses space.

L_t , the third component, contains the matrix :

(8)

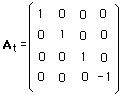
which reverses time.

L_st , the fourth component, contains the matrix :

(9)

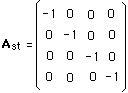
which reverses both space and time.

From the Lorentz group one builds the Poincaré group G_p, whose element is :

(10)

 
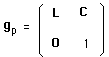
C is a space-time translation :

(11)

 
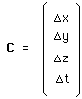
...If we use the four components of the complete Lorentz group L , (10) will be called the complete Poincaré group. As the Lotentz group, it owns four components :

- Its neutral component :

(12) (4212)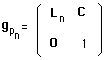

built with the neutral component L_n of the Lorentz group L.

- A second component :

(13)

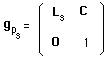
built with the component L_s of the Lorentz group.