Dissiper une idée fausse. Apporter des précisions.

L'image est jolie, séduisante, mais, en tout cas chez moi, elle a enkysté une idée fausse dont j'ai eu un mal fou à me débarrasser.

Le verbe suivre évoque une démarche. On suit une route, une personne du regard, l'évolution d'un point sur une courbe.Il ne viendrait à l'idée de personne de "suivre un point".

Quand Souriau écrit donc que le moment suit le mouvement comme son ombre, on est tenté d'imaginer ceci :

(202)

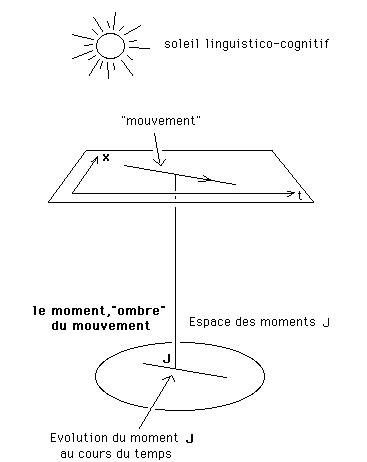
L'idée fausse.

Là, vous avez tout faux. Un mouvement, c'est un moment, un point de l'espace des moments :

(203)

 
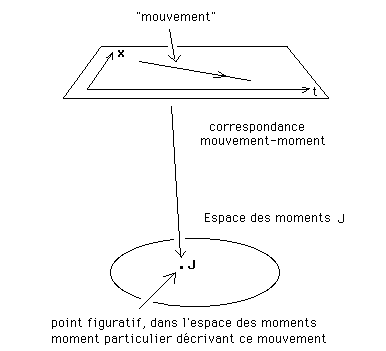
La bonne image.

On a déjà dit qu'avec tous ces groupes : Galilée, Bargmann, Poincaré, Poincaré étendu, les points masses n'étaient soumis à aucune force. Ils allaient donc en ligne droite. Leur trajectoire, du moins telle que nous la percevons ( ce qui implique l'émergence de cette bizarrerie nommée passage, dont nous avons déjà suffisamment parlé ) implique des paramètres comme :

- Energie E
- Impulsion p
- Tournoiement.

On n'est pas maître du module du tournoiement ( dans un référentiel lié à l'objet ) puisque cela devient alors le vecteur spin, dont le module est fixe.

Par contre (du moins pour une particule à masse non-nulle), dans un ensemble géré par le groupe de Bargmann, et si on a fixé le spin s , v est un paramètre libre.

Simplifions. Considérons l'ensemble des mouvements possibles d'une particule de masse m, ayant un spin s donné , et des vecteurs spin s de mêmes orientations. Disons que l'énergie de la particule est son énergie cinétique :
 

 
énergie liée à l'impulsion m v .

 
Les différents mouvements ne dépendent que d'un seul paramètre, la vitesse v . Je schématise.. Mais, graphiquement, en considérant une famille de mouvements d'un même particules, correspondant à des trajectoires rectilignes passant par un même point, avec des modules de vitesse v différents, on aurait :

(204)

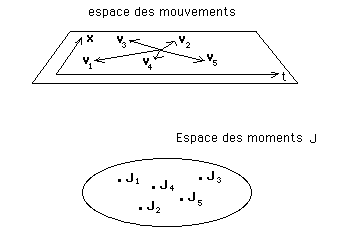
  (J'ai mis les moments n'importe où.)

Ceci étant, tous ces mouvements se réfèrent à la même particule de masse m. Ces particules, qui vont dans des directions différents, à des vitesses différentes, sont de même espèce .