Application à ce qui est ci-dessus :

(197)

 
On a utilisé la propriété évidente : la transposée de la transposée d'une matrice est la matrice de départ.

Donc, globalement :

(198)

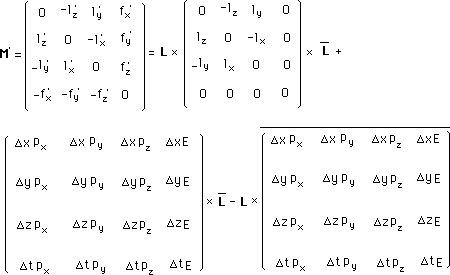
Si je prends une particule à masse non-nulle, je peux toujours me dire que je l'ai cueillie sur l'arbre de la connaissance des états de repos et de non-repos, avec une impulsion nulle.

J'ai vu que je pouvais aussi me débrouiller pour annuler le passage, en me situant dans un référentiel qui "accompagne la particule dans son mouvement".

(199)

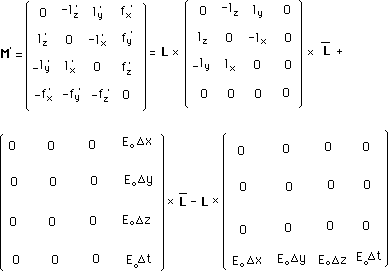
Je ne saurais prendre une particule doté d'une énergie au repose Eo nulle. Cela n'aurait pas de sens physique. Mais je sais aussi, ou suis censé savoir qu'une particule ne saurait avoir un tournoiement (spin) nul, même dans un hypothétique état de repos. Par ailleurs, non seulement ce tournoiement,ou "vecteur spin s", existe toujours, mais son module s est invariant, c'est même une caractéristique de la particule. C'est un multiple demi-entier de h/2p , de la constante de Planck réduite. C'est aussi une conséquence de la "quantification géométrique" inventée par Souriau.

Toujours de la géométrie...
 

Ces "attribut-là" sont un peu plus déconcertants que les attributs non-relativistes, évoqués plus haut.

Mais il faut noter que cette "quantification géométrique" s'applique aussi au monde non-relativiste ( groupe de Bargmann ), en quantifiant le tournoiement, le moment cinétique individuel, la "vorticité", le spin, peu importe le nom qu'on lui donne, de la particule, du points matériel, du truc, du machin géré par le groupe. Ca peut changer de direction mais :

Tout ceci passe par une variable additionnelle z , considérée par certains théoriciens et mathématiciens comme "un intermédiaire de calcul".

Ceci étant, dans cet espace à cinq dimensions :

on se transporte, on se déplace.

Il y a des choses qui ne posent pas de problème, comme :

 
qui correspond à une P-symétrie . Si on l'applique non à un objet ponctuel,mais à un ensemble de points liés, les structures sont être transformées en leur énantiomorphe, en leur image en miroir. Mais, pour une particule isolée, il ne s'agit que d'un "autre mouvement".

 
Toujours en restant dans le 5d on a vu que des attributs s'étaient dégagés.

En non-relativiste

En relativiste :

 Ce sont de simples scalaires. Le mathématicien dira qu'ils peuvent être choisis tout aussi bien positifs que négatifs. Ce ne sont que des choix effectués dans un espace de moments particuliers, constituant l'espace des moment, dépendant de n paramètres ( n étant égal à la dimension du groupe ). Dans le moment lié au groupe de Poincaré ( non étendu ) :

(200)

 les paramètres peuvent à priori prendre toutes les valeurs possibles, positives ou négatives.

Soit  J l'ensemble des paramètres qui définit le moment. J est l'espace des moments. Dans cet espace on devrait pouvoir alors distinguer deux domaines :

(201)

Le groupe "surplombe" cet espace et assure les transports divers et variés. Il contient ainsi des éléments qui permettent de transformer des mouvements les uns en les autres. Comment dit Souriau :