On a vu qu'on pouvait annuler le passage f , selon la première idée : en imaginant que le point matériel s'éloigne ( ou de rapproche, en tout cas bouge à la vitesse v et que ceci produit pendant un laps de temps e = Dt un déplacement c = v Dt ).

Dans l'optique inverse ça serait l'observateur qui se déplacerait à une vitesse v et qui couvrirait le trajet c = v Dt pendant le laps de temps Dt .

Oublions donc le passage, qui peut toujours être annulé en accompagnant la particule dans son mouvement , en liant vitesse v et chemin parcouru c .

Mathématiquement, c'est simplement un sous-groupe, celui des transports où on a eu la faiblesse de vouloir relier vitesse, temps et chemin parcouru, où le loch, le chronomètre de bord et l'indicateur de vitesse ont des graduations qui ne sont pas complètement indépendantes.

 Physiquement raisonnable.

 
Il reste ces étranges mouvements souterrains, cette adjonction d'une quantité f à une dimension additionnelle z . Le "souterrain quantique", un de ces aspects de la lanterne de projection platonicienne, à laquelle nous sommes censés ne pas avoir accès.
Bon....

Revenons maintenant au groupe qui gère le déplacement du point relativiste, le groupe de Poincaré.

(182)

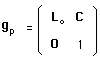
version "orthochrone", standard. Son moment est :

(183)

(184)

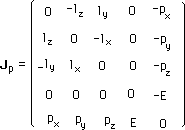
Décompte : dix. Mais j'aurais aussi bien écrire :

(185)

J'ai construit l'action coadjointe. Je sens comment le nouveau "point matériel" se transporte, de manière relativiste, cette-fois. Je sais que dans ces composantes du moment il y a un scalaire nommé énergie E. Mais la masse s'est évaporée. Ou, plustôt, elle a été absorbée par l'énergie.

Masse et énergie sont devenues "la même entité", dite énergie-matière . Il était alors normal qu'il y ait besoin d'un seul scalaire pour décrire cet  état de chose

Là encore, je me pose la question. Y aurait-il une espèce "d'état fondamental" ( tout relatif, d'ailleurs, relatif à un observateur qui se croît, lui aussi, dans ce même "état fondamental" ).

J'ai l'expression de mon action coadjointe :

(186)

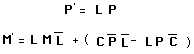
Pour la première ligne, en détaillant :

(187)

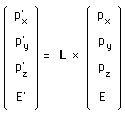
S'il s'agit d'une particule de masse non-nulle, je peux imaginer que dans cet état fondamental, relatif, son impulsion initiale ait pu être être nulle. Il s'agira d'une "particules au repos", qui possèderait donc une énergie au repos Eo :
 

Je pourrais donc communiquer à cette particule une impulsion en faisant agir dessus l'élément du groupe de Lorentz, selon :

(188)

.

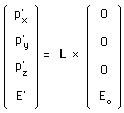
opération qui serait inconcevable avec une "particule à masse nulle", photon ou neutrinos, qui vont à la vitesse c, donc "bougent tout le temps". Ce sont des particules qui ne connaissant jamais le repos. Elles sont toujours une impulsion p , qui se trouve d'ailleurs liée à leur énergie E.

Le physicien non-relativiste, en traînant les pieds, trouvera un peu bizarre qu'une particule qui ait une masse nulle puisse quand même posséder une impulsion.

Mais il s'agit d'un objet mathématique, s'écrira le physicien relativiste, qui écrira :

(189)

 et s'en fout éperdument.

Il reste la seconde relation :

(190)

à essayer de décrypter, si faire se peut.

C est la translation spatio-temporelle ( Dx , Dy , Dz , Dt )

(191)

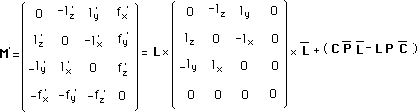
Continuons à détailler.

(192)

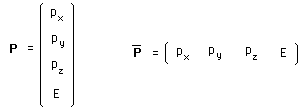
(193)

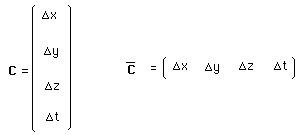
(194)

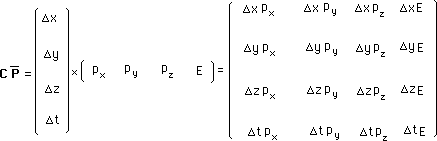
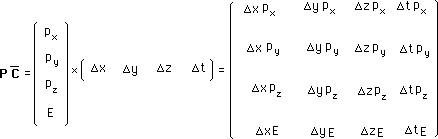
Tiens ! C'est la transposée de la précédente.

 
Le mathématicien dirait, c'est évident, en fonction du théorème suivant (que vous retrouverez par vous-même à titre d'exercice) :
Soient deux matrices dotés de tels format qu'elle soient multipliables. On a :

(196)

La transposée d'un produit de deux matrices est égal au produit de la transposée de la seconde par la transposée de la première (on inverse l'ordre).