

 |
7
|
Un élément gp du groupe de Poincaré
Gp est défini par une suite de paramètres {pi},
dont, nous l'avons déjà dit, le nombre représente la
dimension du groupe . La matrice dg
(g = e) est constituées avec les quantités
{dpi} . L'application
ci-dessus est donc du type :
(81)
![]()
Autrement dit, à une ensemble de scalaires dpi on fait correspondre un nombre égal de scalaires dpi'. La dualité consiste à postuler l'invariance d'un scalaire, selon :
(82)
n étant la dimension du groupe (dix, pour le groupe de Poincaré). Les scalaires Ji représentent les composantes du moment, de même nombre.
Nous déciderons de décomposer ce moment J en deux objets. Le premier sera une matrice M anti-symétrique de format (4,4), donc ayant six composantes, et le second un "quadrivecteur" P, matrice de de format (4,1) :
(83)
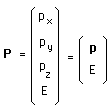
(84)
(85)
Tr signifiant "trace de", et nous aurons encore :
(86)
forme linéaire dont l'invariance assure la dualité.
avec :
(87)
(87c)
mais GG = 1 donc ceci vaut :
(88)
Identifions les termes en y
(89)
C'est à dire :
(90)
----> Là encore suivent des détails de calcul matriciel. Si vous le souhaitez, en cliquant ici vous pouvez aller directement au résultat
Dans la trace on peut effectuer une permutation circulaire
des termes.
(90a)
(90b)
![]()
(90c)
le deuxième terme du second membre est égal au produit d'une matrice ligne par une matrice colonne.
Ceci est égal à la trace du produit inversé
(ci après, schématiquement, le produit d'une matrice ligne par
une matrice colonne):
(90d)
Dans cette trace, je peux opérer une permutation
circulaire :
(90e)
D'où :
(90f)
(90g)
![]()
Ici on va appliquer de nouveau le théorème sur les traces des matrices qui sont le produit d'une autre matrice par une matrice symétrique.
Toute matrice peut être symétrisée
ou antisymétrisée. De plus la trace du produit d'une matrice
par une matrice symétrique est nulle.
(90h)
Je peux appliquer cela à la matrice (90i) ![]() puisqu'on prend la trace
puisqu'on prend la trace
(90j)
![]()
(90k)
mais :
(90l)
donc
(90m)
et :
(90q)
finalement :
(90r)
En regroupant et en changeant les prime de côté l'obtiens mon action de groupe :
