

 |
2
|
3 - Troisième axiome de groupes : Tout élément doit posséder un inverse, noté g-1 , défini par :
Dans notre exemple, ceci s'écrit :
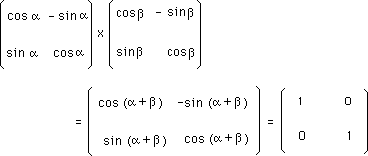
c'est à dire b = - a ou :
...Ici, le calcul de la matrice inverse s'imposait comme une évidence. Mais il n'en est pas toujours ainsi, loin s'en faut. Que faut-il alors pour que toute matrice de l'ensemble considéré possède un inverse, qu'elle soit inversible ? Il faut et il suffit que son déterminant soit non-nul (et nous renvoyons le lecteur à son cours d'algèbre linéaire). Un théorème dit que le déterminant d'un produit de matrices est égal au produit des déterminants de celles-ci. La définition même du déterminant fait que celui d'une matrice diagonale est égal au produit des termes qui la composent. Par exemple :

Conséquences : le déterminant de toutes les matrices unité 1 vaut 1. Donc :
conséquence : une matrice à déterminant nul ne peut posséder d'inverse, ce qui contredirait s définition. Par ailleurs :
4 - Quatrième axiome des groupes : l'opération de composition doit être associative :
C'est toujours le cas....
Dimension d'un groupe :
...Une petite parenthèse sur la dimension d'un groupe (de matrices), qui n'a rien à voir avec le rang des matrices le composant ou le nombres de quantités constituant "l'espace sur lequel agit ce groupe" ( par exemple l'espace (x,y) à deux dimensions ou l'espace temps (x,y) à quatre dimensions).
...Nous
avons ici un exemple d'une famille de matrices carrées à un
seul paramètre a, dont il se trouve qu'elle forme un groupe. On trouvera
plus loin des groupes constitués de matrices carrées définies
par n paramètres : six, dix, seize, n'importe quoi.
Le
nombre des paramètre servant à définir les matrices carrées
du groupe sera appelé dimension du groupe.
Nous avons ici affaire à un groupe constitué par une famille
de matrices à un paramètre a. La dimension de ce groupe est
1.
Notons au passage que :
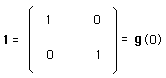
Remarque :
...Les groupes, et les groupes qui nous intéressent ici, ne sont pas automatiquement commutatifs. C'est même l'exception. Il se trouve que notre groupe-exemple est commutatif :
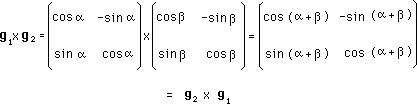
...On aura reconnu dans ce groupe les matrices de rotation 2d, autour d'un axe fixe. Dans "le concret" cette opération est "évidemment commutative". Faire tourner au tour d'un axe :
- D'abord d'un angle a , puis d'un angle b
ou :
- D'abord d'un angle b , puis d'un angle a
conduit au même résultat.
Vous me direz : "normal. Les groupes de rotations sont essentiellement commutatifs".
...Faux. C'est une propriété du 2d. En 3d, ça ne marche plus. Considérez un groupe particulier, constitué par l'ensemble des rotations autour de trois axes orthogonaux (OX,OY,OZ).
Exercice : vous montrerez, en prenant un objet et en lui faisant subir :
- D'abord une rotation de + 90° autour de OX
- Puis une rotation de
+ 90° autour de OZ
puis les mêmes
rotations, mais dans un ordre inverse, que vous ne parvenez pas au même
résultat. Cette opération est non-commutative.
Action d'un groupe.
...Un groupe G est constitué d'un ensemble de matrices carrées. On peut déjà considérer qu'il agit sur lui-même ( voir plus loin les axiome définissant un action de groupe , concept essentiel).
...Notre groupe-exemple peut aussi agir sur les points d'un "espace 2d". On dira qu'il les fait tourner. Un groupe, c'est fait pour transporter, mais transporter quoi au juste ?
...Eh bien justement, ça n'est pas ce qui est important. Citant son ouvrage "Grammaire de la Nature", nous dirons, avec J.M.Souriau que :
La façon de transporter vaut mieux que ce que l'on transporte.
Dans le cas de notre groupe-exemple, les matrices agissent sur un espace 2d (x,), et on pourra écrire l'action correspondante
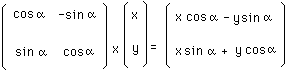
Si on pose ( matrice-colonne ) :
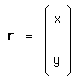
alors l'action s'écrit simplement :
g x r
...Dans ce cas particulier l'action de notre groupe sur l'espace (x,y) s'identifie avec la multiplication matricielle. Mais nous voulons montrer qu'il ne s'agit que d'un action particulière et que le concept d'action , fondamental en physique, est beaucoup plus général.
Retour vers le sous-sommaire "groupes et physique"
