Mathématiquement, la solution présentée est sans points d'ombre. On a simplement négligé la pression d'entrée de jeu dans les équations de champ, dans le tenseur T, qui devient :

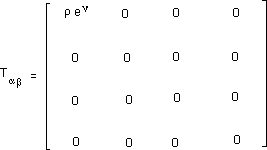
ce qui signifie que :
 

 
p est, dimensionnellement parlant, une densité d'énergie, en joules par mètres cubes. rc² aussi. Si le milieu était gazeux, cela signifierait par exemple que la pression est la mesure de la densité d'énergie cinétique, liée à une vitesse moyenne d'agitation thermique <V> . Supposons que le milieu intérieur puisse être assimilé à un gaz parfait. Alors la pression de matière s'écrirait :

On voit que l'approximation effectuée revient alors à supposer que la vitesse d'agitation thermique dans l'objet est non relativiste. Ce modèle est donc bon pour décrire des astres "ordinaires", y compris des étoiles entourées de vide, à symétrie sphérique, qui ne tournent pas sur elles-mêmes. Cette solution est différente de celle développée antérieurement et qu'on trouvera décrite par exemple dans l'ouvrage de Adler, Schiffer et Bazin : Introduction to general relativity, 1975, Mac Graw Hill books. D'emblée, cette solution est alors conçue pour gérer un milieu à pression non-nulle. On négocie le raccord entre la métrique extérieure et la métrique intérieure en faisant p = 0 à la surface de l'astre. On obtient alors la métrique :
 

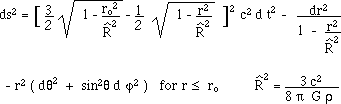
On remarquera que si l'on fait alors des développements en série en supposant :

 
les deux métriques (celle-ci et la nôtre) se rejoignent asymptotiquement. De toute manière, quand on suppose la pression non nulle, il manque une équation d'état p = p(r). Mais le travail débouche sur la fameuse équation TOV (Tolmann, Oppenheimer, Volkov), qui est une équation différentielle en (p , p' , r) où p' désigne la dérivée spatiale de la pression.

m est la fonction m(r) :

(voir l'article, ou les ouvrages). Cette équation est classiquement utilisée pour donner une description de l'intérieur des étoiles à neutrons, où ont y fait simplement r = constante (de l'ordre de 1016 g/cm3) . On obtient alors une équation différentielle donnant l'évolution de la pression. A noter que lorsque l'étoile voit sa masse croître, ce qu'elle censée faire à densité constante, puisque cet entassement de neutrons est supposé incompressible, la première criticité qui apparaît concerne la pression, qui prend une valeur infinie au centre, alors même que le rayon de l'astre est encore supérieur à son rayon de Schwarzschild. Nous avons, bien sûr, tenté de mettre en œuvre une solution analogue, pour les deux métriques conjuguées. Physiquement, le problème est déconcertant. Dans le feuillet où se trouve l'astre, supposé par exemple être le feuillet F, le nôtre, on a deux fonctions scalaires p(r) et r(r) qui sont censées décrire le champ de pression et la densité dans l'étoile à neutrons, avec r(r) = constante. Dans la mesure où la géométrie dans le second feuillet découle alors de l'équation :
 

ces éléments p(r) et r(r) sont alors présents dans le second membre. Pourtant le second feuillet est censé être vide (r* = 0) et à pression nulle (p*=0). Mais la structure choisie, le système des deux équations de champ couplées, fait que ces termes contribuent à la géométrie de l'autre feuillet.

Lorsqu'on met en œuvre la machinerie classique, on retrouve des équations semblables, qui se déduisent finalement du formalisme classique en changeant simple r en - r et p en -p . On trouve également une équation TOV. Mais cette équation différentielle doit impérativement donner la même solution. Il ne peut y avoir deux équations différentielles différentes donnant p(r). Or l'équation à laquelle on aboutit est différente. Elle correspond simplement au changement global :

  avec :

Or l'équation différentielle TOV n'est pas invariante par ce changement et on obtient alors :

 
(le signe moins au dénominateur se change en signe plus). Il y a donc inexistence de solution, à pression non nulle, du moins selon cette approche, inspirée de l'approche classique. Loin de nous décourager, ce constat nous semble être l'indice que le problème doit être abordé différemment, ce que nous tenterons dans des travaux ultérieurs, consacrés à l'étude de l'approche de la criticité dans une étoile à neutrons. Nous avons développé un modèle de l'ère radiative, qui correspond au papier Geometrical Physics A, 6 , et où les constantes de la physique sont censées être en quelque sorte indexées sur la valeur de la pression de radiation. Lorsqu'on remonte en déça de l'époque du découplage, dans le modèle standard, on arrive d'ailleurs à des conditions où non seulement la contribution de la pression au champ cesse d'être négligeable, mais où cette contribution est alors essentielement due au rayonnement. Ceci signifierait que les constantes de la physique dépendraient de la densité d'énergie électromagnétique, alias pression de radiation.

Nous avons donc commencé une approche d'une étude de l'étoiles à neutrons, où le terme :

n'est plus négligeable devant r , en supposant que les constantes de la physique (G , h , c , la masse du neutron, plus les autres constantes) dépendent alors de la valeur locale de la pression (on étudie une solution supposée stationnaire, en équilibre). Comme l'entrée en criticité de l'étoile commence par l'envolée de la pression au centre, et que dans cette optique la valeur locale de la vitesse de la lumière suivrait cette montée, des conditions où c est infini devrait aller, selon nous, avec une rupture de la topologie de l'espace temps, au cœur de l'astre. Tant que p et c restent finis, celle-ci reste hypersphérique, c'est à dire qu'un peut "peler" l'étoile à neutrons jusqu'en son centre. Il y a toujours de la matière et on est toujours dans le même feuillet. Mais, et nous travaillons dans cette voie, la montée de la valeur locale de c vers une valeur infinie devrait entraîner un changement de topologie, la géométrie au centre de l'étoile se modifiant, avec apparition d'un "pont hypertorique", passage entre les deux feuillets. La matière s'y écoulerait alors à vitesse relativiste. Nous avons envisagé deux options possibles. Soit l'apport de matière ferait entrer l'étoile en criticité relativement lentement (absoption de vent stellaire issu d'une étoile compagne, par exemple). Alors ce pont hypertorique pourrait conduire à une situation quasi stationnaire, en agissant à la manière d'un trop-plein. L'étoile évacuerait par ce passage, en continu, l'excès de matière qu'elle reçoit de sa compagne.

Mais, seconde option, un apport plus rapide avec une entrée plus brutale en état de criticité (par exemple lors de la fusion d'un système double, constitué de deux étoiles à neutrons) la stationnarité ou quasi stationnarité ne pourrait plus être invoquée et il faudrait alors essayer de construire un scénario encore spéculatif : le transfert hyperspatial rapide d'une part importante de la masse, en direction de l'autre feuillet.