(33- b)

(33- c)

(33- d)

...From (33-b) and (33-d) the curvature indixes k and k* must be negative, then we get, with k = k* = - 1 . The initial evolution laws are simply linear: R = R* » r. But, as will be shown later the metter densities may become different. Then we get the system :
(34-a)

(34-b)

(34-c)

(34-d)

from which we get immediatly :

(35-a)

(35-b)

 
Introducing the mass-conservation in both folds :
(36)

Then the system becomes :
(37-a)

(37-b)

...Notice that R = R* gives R" = R*" = 0. On another hand, if the two universes were "fully coupled", i.e. R*/R = constant, then they would correspond to Friedmann models, with "parallel evolutions". But we consider that they are coupled by gravitational field, through (37-a) and (37-b) that show that the linear expansion is unstable. If, for an example, if R > R* then R" > 0 and R*" < 0 . The system can be numerically solved. The typical solution corresponds to figure 1.

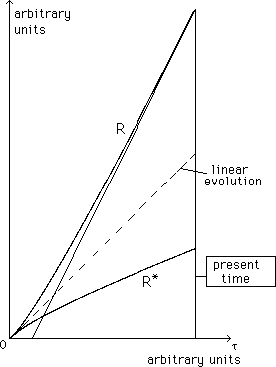
There is a "common history", described though the common sytem of coordinates :

...Using (13) to (16) we may return to the systems { t , r , q , j } and { t* , r* , q , j }. Notice that the velocities of the light velocities c and c* and the characteristic time T and T * may be different.
If c = c* and T = T* = 1 we get simply (t = t ; t* = - t)

Why can’t we take simply r* = r * ?
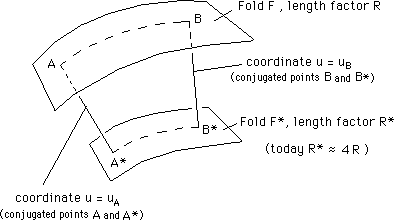
Because lenghts scales R and R* are found to be different. Consider two sets of conjugated points (a , A*) and (B , B*). Assume (qA = qB ; jA = jB). The two sets correspond to radial marker uA and uB. As they are conjugated, A and A* refer to the same radial marker uA . Same thing for conjugated points B and B*, corresponding to uB value. The distance AB is R (uB - uA) , while the distance A*B* is R* (uB - uA). They are different, for R* ¹ R .

... If one assumes that the coordinates (t , x , y , z) and (t* , x* , y* , z*) refers to two observers, located in folds F and F*, they are like two men observing the same movie, in two distinct rooms but :

- the screens have different sizes (R and R*).

- the orders of the events are opposite (t and t* have opposite signs)

- what is "right" on one screen is "left" on the other one
(enantiomorphy)