...When a (positive) mass m* is present in the fold F*, it shapes the geometry in the fold F*. As presented first in reference [6] the geometry in the adjacent portion of the fold F , solution of the equation :

(19)

can be described by a Schwarzschild solution :

(20)

where the constant v is negative.

(21)

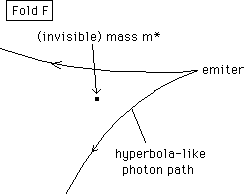
...The mass m*, present in the fold F*, where it attracts a mass m*, repels a mass of the other fold F, the geodesic being hyperbola-like.

(22)

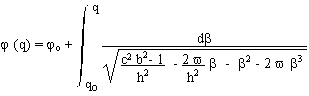
The null geodesics can be calculated.

j = polar coordinate. q = 1/r . b and h are trajectory parameters. The null geodesics are :

(22)

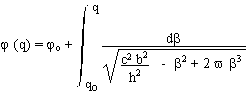
The light pathes, hyperbola like, correspond to figure 6. We get a negative gravitational lensing.

...In figure 7 we have schematically figured light paths, focussed by the action of a non-homogeneous mass distribution r* of the fold F*, reinforcing the positive gravitational lensing due to the galaxy. The photon trajectory is straight if it travels through an homogenous medium.

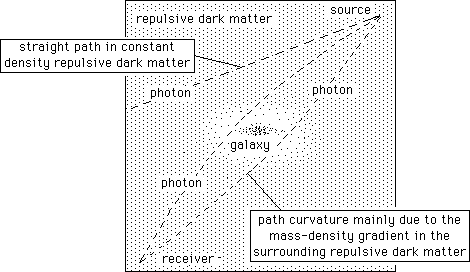
...Classically one considers the observed strong gravitational lensing effects as a proof of the existence of attractive dark matter in our Universe. We suggest this could be mainly due to basically invisible repulsive dark matter, surrounding the visible structures (more precisely to the gradient of the repulsive dark matter, at the vicinity of the galaxies).
 

Conclusion.

...We consider the Universe as the site of interaction of two populations : normal matter m and repulsive dark matter m*, the dynamics of the system corresponding to :

- m attracts m

- m* attracts m*

- m and m* mutually repel

through newtonian (and anti-newtonian) laws. Then the repulsive dark matter behaves as if it owned negative mass (and negative energy). We build a model of a galaxy located is some sort of a hole, in a surrounding repulsive dark matter environment, which confines it. We show that we refind good looking rotation curves.

...We avoid the problem of the negative mass and negative energy, introducing a new geometric framework, the Universe being composed of two folds, considered as the two-fold cover of a "skeleton manifold", which provides an involutive mapping linking two conjugated points (M,M*). The geometry of the fold F is described by a metric g and the one of the fold F* by a metric g*. Both are linked through a system of two coupled field equations. On geometrical grounds, any structure located in a fold is invisible from the second one. We build a cosmological model, assuming that the two universes are homogeneous and isotropic. During the radiative era we assume the mass densities r and r* and the pressures p and p* are respectively equal. Then the model identifies to the standard one. When matter (and repulsive dark matter) dominate in both folds (we assume decoupling occurs at the same moment in both worlds), the two evolutions are different. One universe (supposed to be ours) expands faster than the other one. The impact of the repulsive dark matter world on the evolution of ours is similar to the introduction of a cosmological constant in the Einstein field equation, so that it makes it possible to adjust the age of the Universe to recent measures of the Hubble’s constant. With a today’s mass-density ratio r*/r = 64 we find an age equal to 15.7 billions years.

...Negative gravitational lensing, due to the gradient of geometrically invisible surrounding repulsive dark matter may induce the same effect as the gravitational lensing attributed to attractive dark matter.
 

References.

[1] M.Myamoto and R.Nagai Publ. Astrom. Soc. Japan 27, 583, 1975
[2] S.Chandrasekhar : "Ellipsoidal Figures of Equilibrium". Yale University Press, New Haven and London, 1969
[3] J.Binney and S.Tremaine, "Galactic Dynamics", Princeton University Press, Princeton, 1987.
[4] Bahcall J.N & Soneira R.M. APJ. S 44 p. 73 1980
[5] Bahcall J.N. , Flynn A and Gould A. APJ 389 p.234 1992
[6] Petit J.P.: The missing mass effect. Il Nuovo Cimento B Vol. 109 July 1994, pp. 697-710
[7] Petit J.P. : Twin Universe Cosmology. Astr. And Sp. Sc. 226 : 273-307, 1995
 

Achnowledgements :

The author thanks Pr. J.M.Souriau for useful advices and comments.
This work is supported by the french CNRS and by the A. Dreyer Brevets et Développement company.
Déposé sous pli cacheté à l'Académie des Sciences de Paris, 1998.