repulsive dark matter

Repulsive dark matter (p3)

...

If we assume the thermal velocities, in both folds, to be negligible with respect to the velocity of the light, the pressures can be neglected (zero-pressure dust universes model). In a first step, when decoupling has just occured, we assume

r = r

* and the system becomes :

(12-a)

(12- b)

(12- c)

(12- d)

...From (12-b) and (12-d) the curvature indices k and k* must be negative. The evolution laws are simply linear : R = R* » t

...After that short period (the very begining of the matter dominated era), we return to the system (11-a) to (11-d), with curvature indixes k = k* = -1 :

(13-a)

(13- b)

(13- c)

(13- d)

from which we get immediately :

(14-a)

(14-b)

Introducing the mass-conservation in both folds :

(15)

r R3 = r* R*3 = ro Ro3 = constant

ro and Ro being characteristic quantities. Let :

(16)

(17)

Then the system becomes :

(18-a)

(18-b)

...Notice that R = R* gives R" = R*" = 0. On another hand, if the two universes were "fully coupled", i.e. R*/R = constant, then they would correspond to Friedmann models, with "parallel evolutions". But we consider that they are coupled by the gravitational field, through (18-a) and (18-b) that show that the linear expansion is unstable. If, for example R > R* then R" > 0 and R* " < 0 . The system can be solved numerically. The typical solution corresponds to figure 5.

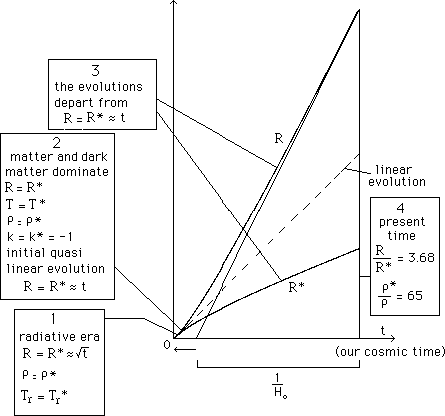
Fig. 5 :The evolution of the scale parameters

of the universe and dark universe.

...With respect to the classical Friedmann model, this new model enlarges the age of the universe. Depends on the retained value of the Hubble constant Ho. In 1993 measurements from Hubble telescope enlarged the constant from 45 to 70 km/s/Mpc which, based on the Einstein de Sitter model with zero cosmological constant, gave an age of the universe lying between 8 and 9 billions yrs, and arose a sever problem with respect to the age of the oldest stars of our galaxy. But more recent calibration of cepheids, from Hipparcos satellite measurements, lowered Ho . At the same time some people tended to low the estimated age of the oldest stars of our galaxy.

...Notice that the repulsive dark matter plays the role of a "cosmological constant", for it gives a positive acceleration R" in our fold.

Anyway, the discussion about the age of the universe is not ended.