univers gemellaire jumeaux cosmologie

Matter-ghost matter astrophysics. 7 : Confinment of spheroidal galaxies by surounding ghost matter.(p2) .

2) The origin of the Newton law and Poisson equation.

The Newton law is an hypothesis, a principle. It works. Proof : we can compute the trajectories of the planets, quite well, and send satellites at large distances, with a sharp precision.

The Einstein field equation is an hypothesis, a principle.
(7)

S = c T

It works. Proof : We can compute the displacement of the perihely of a mass, a satellite orbiting in the field created by a heavier mass. If we would live close to a neutron star and if this object had a companion, we should observe the path shown on figure 4.

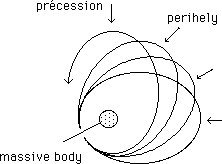
Fig.4 : Precession of the perihely of the trajectory of a companion,

orbiting around a very massive body.

The measurement would confirm the theory, as we do for the case of Mercury. By the way, this phenomena is compatible with the matter ghost matter model.
(8)

S = c (T - T*)

(9)

S* = c (T* - T)

We are supposed to live in a region of the universe where matter dominates ( T* << T ) , so that the field equations system becomes :
(10)

S » c T

(11)

S* = - c T

When Einstein introduced the new concept of field equation one checked if such formalism was compatible to the Newton law. Classically one considers the metric as close to one describing an homogeneous medium (r = constant). Then a mass concentration is considered as a small perturbation :
(12)

g = g_o + e g

g_o refers to this constant density medium. e being a small parameter, the second term e g represents the pertubation. The second member of the field equation is assimilated to :
(13)

But, and this is very important, the two terms g_o and e g are chosen time-independent. Then one computes the left hand of (7) through the expansion into a series (12) and find :
(14)

which can be written
(15)

and is identified to Poisson equation, through :
(16)

From this we also define the gravitational potential :
(17)

g_oo being one of the metric potentials. But all this is performed is steady state conditions. We need it to define the first order term g_o , chosen lorentzian :
(18)

ds² = c² dt² - dx² -dy² -dz²

This a good approximation if we deal with :

A portion of the universe

- where a mass concentration is surrounded by void.

- where the velocities are small with respect to c

- where he local curvature is weak

Then, is it convenient to describe an infinite medium ? No. To do that, to set up a Poisson equation, applying to a constant density infinite medium we need a non-steady zeroth order solution

g_o

, which cannot have a Lorentz form. Must be something like a Friedmann solution. If the medium is fully homogenous, if the non steady mass density is constant over all space, there is no perturbation term.

g_o

is simply a Robertson-Walker solution, giving Friedmann models (for classical general relativity).

Where is the gravitational potential Y , for such infinite medium, with mass density constant over space ? No where. It does not exist and we cannot define such scalar quantity.

Then, for an infinite constant density medium, whatever is is constant in time (that should not be physical) or time-dependant (Friedmann) the Poisson equation becomes a pure theoretical phantasm. It simply does not exist. It has no physical meaning. We cannot invoke it

Then, how is the gravitational filed around an arbitrarly chosen point in space ? Our answer : zero.

The reader will say : What about the screen effect in electrostatic ?

Can you deal with an infinite, constant electric charge density re medium ? Not physical. Such a medium should expand immediatly, at tremendous velocity, if the charge density departs significantly from equilibrium (n + = n - ).

Another reader will argue :

- In 1934 Milne and Mc Crea refound the Friedmann equation, just starting from Euler and Poisson equations.

What does it means ? Simply that the collapse, or expansion of a dust (zero pressure) ball obeys the same equation that a constant density universe, corresponding to Friedmann model. Nothing else.