...In 1916 Eddington derived a spherically symmetric steady-state solution, combining the Vlasov and the Poisson equations. He assumed that the ellipsoid of the velocities was spherically symmetric and pointed towards the center of the system.

Eddington derived the following relation between the mass density and the gravitational potential

(20)

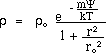
which represents a steady-state distribution of matter in a collision-free gas, in a gravitational potential Y, in which the gravitational force balances the pressure force. Let us take the same kind of a solution for the antipodal region

(21)

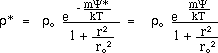
So that we have to solve the following equation

(22)

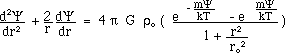
Take

(23)

Introduce the following adimensional quantities :

(24)

We get

(24)

which can be solved by numerical computation. We can take the following initial conditions

Figure 2 : Spherically symmetric Eddington-type solution. The gravitational potential

Figure 3 : Spherically symmetric Eddington-type solution. Mass densities. If a cluster exists in one fold, an associated diffuse halo exists in the conjugated region of the second fold.