Abstract

...A new field equation is proposed, associated to a S3 x R1 topology. We introduce a differential involutive maping A which links any point of space s to the antipodal region A(s). According to this equation the geometry of the manifold depends both on the energy-momentum tensor T and on the antipodal tensor A(T). Considering time-independent metric with low fields and small velocities, we derive the associated Poisson equation, which provides cluster-like structures interacting with halo-like antipodal structures. The second structure helps the confinement of the first. It is suggested that this model could explain the missing mass effect and the large scale structure of the universe.

1) Introduction

...The equilibrium of a galaxy is studied through a certain set of non-relativistic equations, as for example, Vlasov equation coupled to Poisson equation, which comes from the general Einstein field equation

(1)

plus a steady-state hypothesis in which we take weak fields and small velocities. It is well known that the gravitational field due to the visible mass of our galaxy cannot balance the centrifugal and the pressure forces. Some people assume that some invisible mass, dark matter, may contribute to the field and balance the centrifugal force. In the following we are going to propose another model, based on a new field equation.

 
2) A new field equation

We assume that the universe has the topology of S3 x R1 .
The Gaussian coordinates are

(2)

where x° is a time-marker and the vector s represents the spatial markers. Space-time is oriented. It is possible to define a differential involutive maping linking a given point s to the antipodal point s* .

(3)

...Consider two tensor fields S and T, defined on the manifold. Suppose that they are linked in the following field equation

(4)

with

(5)

...We assume that the light follows the geodesics of space-time. g is the metric tensor. R is the Ricci tensor, so that

(6)

 
We can write the field equation in the more explicit form

(7)

Let us write the tensors T and T* as

(8)

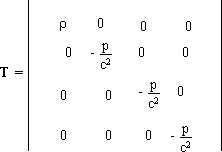
(9)

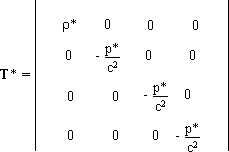
with

 
If we take the zero-divergence condition, the fluid obeys the following conservation equations

(10)

3) Time independent conditions with weak fields and small velocities. The Poisson equation.

We can apply the classical method, taking a quasi-Lorentzian metric
(11)

where h is the Lorentzian metric and e is a small parameter.

In three-dimensional notations

(12)

The newtonian law applies over all space. In addition the gravitational potential is defined as the following :

(13)

...Conversely, given the gravitational potential Y, the motion of a particle will be along a four-dimensional geodesic if the goo terms of the metric tensors has the form
(14)
 

we get
(15)

By identification we get the following Poisson equation

(16)

If we consider a spherically symmetric system

(17)

(18)

From (17)

(19)