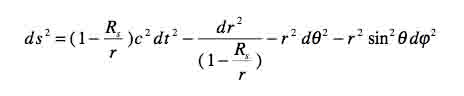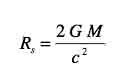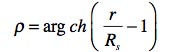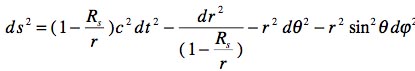Lundi 18 juillet 2016 : L'article mis en ligne sur Researchgate :

L'ensemble des publications mises en ligne : 8000 vues

Un buzz scientifique :

                                                            Pour télécharger cet article à partir de mon site

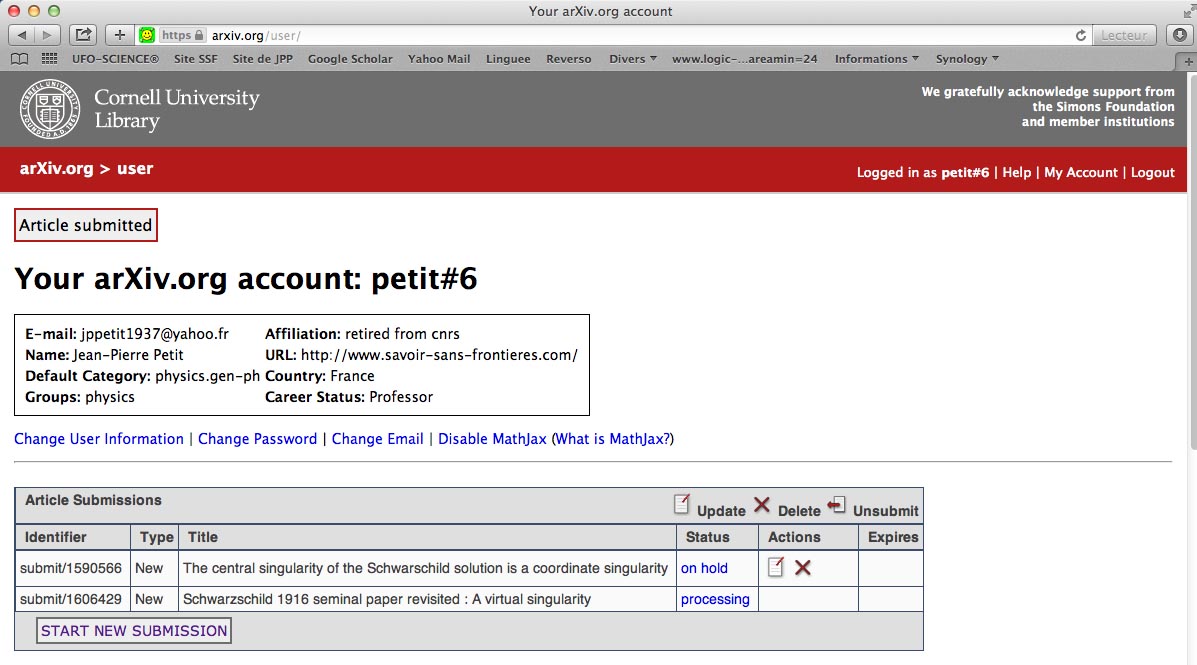
Comme je l'ai montré, ce second article a été immédiatement bloqué sur arXiv :

Mardi 12 juillet 2016 : Fichiers effacés sur arXiv, quelques jours après soumission et envoi du message ci-après :

Traduction :

Les modérateurs ont estimé que les articles que vous soumettez n'avaient pas fait l'objet d'un contrôle suffisant, au point que ceux-ci puissent être considérés comme publiables par un journal conventionnel ( en clair, arXiv est un site de mise en ligne de prepirints, et ce que vous nous adresser ne mérite pas ce qualificatif ).

Et le message se poursuit par

Notez que les modérateurs d'ArXiv ne sont pas des referees et ne sont nullement tenus de produire les arguments sur la base desquels ils decident de rejeter un papier.

Nos modérateurs demandent qu'à l'avenir vous limitiez la soumissions d'articles à ceux qui ont été au préalable publiés dans une revue conventionnelle et "mainstream" (c'est à dire à des articles correspondant au courant de pensée actuel dominant dans la discipline). Des articles qui ne contiennent pas la référence des journaux où ils auraient été préalablement publiés seront systématiquement rejetés.

Si un nombre significatif de vos articles ont été publiés pendant une période aisonnable de temps, nous reconsidèrerons cette décision.

Pour plus d'information sur notre politique de modération, voyez l'adresse ci-après.

Tous les articles que j'ai envoyés à arXiv depuis 3 ans subissent maintenant le même traitement. Celui-ci est le dix-huitième. Il faut savoir qu'étant donné qu'arXiv a une envergure internationale il est hors de question que des centaines de milliers d'articles, dans maintes disciplines, soient "modérés" par les gens de Cornell University. arXiv "sous-traite" donc dans tous les pays et, en France, le sous-traitant d'aXiv est ... le CNRS, lequel confie aussitôt la surveillance des soumissions d'arXiv à des cerbères dans les différentes spécialités.

Me concernant, il s'agit très probablement des Cosmic Men français les plus actifs. L'un d'eux, aussi actif, y compris médiatiquement, que peu productif scientifiquement, sévit déjà sur Wikipedia, où il a été un des principaux acteurs responsables de mon exclusion à vie, il y a dix ans (pour avoir révélé l'identité d'un intervenant, un certain Yacine Dolivet, à l'époque doctorant, qui multipliait les interventions imbéciles, faisant état de son incompétence). On a sauté en fait sur le premier prétexte venu. Là, à arXiv, ces gens ont carrément mis en place des structures de rejet automatique dès que mon nom apparaît : ( IF "Jean-Pierre Petit" ... THEN ....).

Une telle situation relèverait d'une enquête de la part de journalistes scientifiques. Mais aucun ne bougera le petit doigt. Pourquoi ? Parce que cette structure de rejet les toucherait aussitôt. Or les journalistes scientifiques ont besoin d'être alimentés en "nouveautés" par les chercheurs mainstream. Si cette source se tarissant, leur position deviendrait immédiatement très inconfortable. Leur carte de "journaliste scientifique" pourrait éventuellement sauter, menace qui avait été brandie il y a 15 ans contre Martine Castellot. Quand notre livre sera sorti, à l'automne, on verra si un journalisme conventionnel peut mener une enquête, demander au CNRS qui gère arXiv-Cosmologie en France (la section d'arXiv qr-qc, c'est à dire General Relativity and Quantum Cosmology). Peut-on demander à savoir qui a émis ces mails imbéciles et choquants? Le Cnrs opposera sans doute un barrage immédiat, prétextant "l'indépendance de la structure de modération".

                          Affaire à Suivre.

Le CNRS a sa propre structure de mise en ligne de preprints, qui s'appelle HAL. ("archives-ouvertes'....).   Quatre cent mille documents en ligne.  J'ai tenté d'y accéder, mais celle-ci est exclusivement réservée aux chercheurs appartenant à un laboratoire, propre ou affilié au CNRS. J'ai demandé à mon ancien laboratoire, le LAM (Laboratoire d'Astrophysique de Marseille) à figurer sur ses effectifs en tant que "chercheur associé", ce qui était tout à fait faisable administrativement. J'ai rencontré le directeur qui m'a aussitôt opposé un refus catégorique, avant même que je puisse plaider ma cause dans son bureau.

Tout cela est une situation gravissime, vis à vis de l'avenir de la recherche française. Nous pouvons constater que la politique est gérée de plus en plus par des gens qui sont incompétents et nuisibles, comme nos actuels ministres de l'Education Nationale, de la Recherche et des Universités, Najat Belkacem, 38 ans, issue de Science po, recalée à l'ENA (ne connaissant rien à l'enseignement), comme Myriam El Kohmri, 38 ans, ministre du travail (quoique n'ayant jamais ... travaillé, comme Valls et Hollande, politiciens professionnels dès la fin de leurs études). MLyriam el Kohmri : diplôme d'études supérieures spécialisées, ministre du travail. Au coeur de cette responsabilité l'imbécile en chef, notre actuel Président, François Hollande qui, comme son premier ministre, n'a jamais fait autre chose que de la politique. Un incompétent ne peut que s'entourer de ses semblable.

20 juillet 2016 : Cette affaire de coiffeur payé 10.000 euros, confirmé par le Foll, porte-parole de l'Elysée (qui justifie cela en disant que ce type accompagne le Président partout dans ses déplaceents et est de service 24 heures sur 24) est profondément choquante.

Qui dira à ce bouffon " Tu vois ça, connard, ça s'appelle un peigne ! "

On est dans l'inimaginable, surtout dans le contexte actuel, terriblement dramatique. Avant, il y avait l'autre nain de la politique (sur tous les plans) qui salariait grassement une maquilleuse (il est possible qu'Hollande ait reconduit ce poste). C'est tout simplement méprisable. Et ce sont ces clowns qui sont à la tête d'un pays appelé la France ! C'est pitoyable, pathétique.

Il y a pire. Avec ces bataille des différents candidats, pourquoi ne retrouverions-nous pas le duo Hollande- Marine le Pen, au second tour des éléctions présidentielles, avec réelection de ce clown, pour barrer la route à l'extrême-droite .... Un cauchemard...

Valls : " il y aura d'autres attentats du même genre, d'autres victimes innocentes. Le combat contre le terrorisme sera long ".

Lisez ce texte, produit par un jeune homme qui, dans sa tête, est au huitième siècle. Vous saurez à quoi nous sommes confrontés.

Encore quelques attentats du même genre et la France pourra basculer dans la guerre civile. Comment ? Etape suivante : des plastiquages de mosquées. Je dirais même plus : ces attentats contre des mosquées, ça sera peut être DAESH qui les commettra, pour que cette "guerre finale" démarre. Certains pensent au début de la guerre d'Algérie. Au bout " la valise ou le cercueil ". Mais pour qui, pour aller où ?

J'ai entendu hier un responsable politique parler du fait qu'Erdogan songeait à rétablir la peine de mort en Turquie, et qui commentait cela en disant "alors il perdrait toute chance d'intégrer l'Union Européenne".

L'Union Européenne, en pleine guerre civile, un jour ? Pas impossible. Ce " terrorisme sans frontières " peut suffire à allumer cet incendie monstrueux. Autre aspect "moderne" : la propagation des idéologies par Internet, revers de la médaille d'une "modernité". Un autre phénomène totalement incontrôlable.

Ailleurs, on discute du sexe des anges : les transexuels ont obtenu de ne pas être stérilisés. Ainsi des hommes transformés en femmes conserveront leur droit imprescriptible à procréer.

Revenons à la question science :

Ce genre d'incurie frappe également le CNRS, à tous les niveaux. Le fait de demander que les papiers soumis soient "mainstream" (dans le courant des idées du temps) est en soi une complète aberration. Car une idée réellement neuve ne peut pas être "mainstream" (comme celles que je m'efforce de mettre en avant). Jadis cette incurie a marqué la mort définitive de la MHD française, un domaine où, en 1975, j'étais en pointe devant Américains et Russes ! Je me suis totalement détourné de ce domaine de recherche, ce qui ne m'a pas empêché, mettant à profit mes connaissances en matière de plasma, "froids" ou de fusion, de pondre cinq vidéos expliquant pourquoi le projet ITER est une aberration. La première a dépassé les 100.000 vues. Si vous composer ITER youtube sur Google vous la verrez apparaître aussitôt en tête de liste.

Non, les étudiants de l'Ecole Nationale Supérieure de l'Aéronautique n'auront pas de cours sur les entrées d'air contrôlées par MHD et sur la suppression de l'instabilité électrothermique, de Vélikhov. Aucun enseignant n'aurait, en France, compétence pour assurer de tels cours, qui s'inscrivent pourtant dans l'aéronautique de l'avenir.

Le livre nous nous allons sortir à l'automne, Jean-Claude Bourret et moi ( et qui est entièrement finalisé ) contiendra une partie réquisitoire contre ces décisions imbéciles, le Cnrs, le Cnes et l'Armée était désignés comme principaux responsables. Quant aux responsables, qu'ils restent sans inquiétudes, ils ne figurent dans l'ouvrage que par des lettres de l'alphabet.

Ce qui se passe ainsi en Cosmologie, et qui correspond à ce message d'arXiv n'est que l'expression du "mal français".

Je me souviens du calvaire qu'a vécu mon ami Jacques Benveniste à l'INSERM (la Recherche Médicale, version CNRS). Lazare, le directeur de l'INSERM de l'époque lui avait fixé un délai pour prouver ses dires, au terme duquel il a été proprement éjecté de ses locaux et confiné dans des baraques Algeco, dans la cour de son labo, jusqu'à son décès. Il est mort d'épuisement. Alors que c'était déjà un cehercheur confirmé et brillant ... nobélisable. A la place du directeur du Cnrs, réalisant que l'eau était le milieu le plus mystérieux qui soit, j'aurais suscité la création d'une recherche interdisciplinaire sur ce sujet. Je me souviens de la phrase d'un chimiste, responsable au Cnrs, qui avait dit en public devant nous, lors d'un festival "Science Frontières" :

- Moi, je ne sais pas pourquoi l'eau est liquide à la température ordinaire, et cela ne m'empêche pas de dormir

C'est à cause d'imbéciles de ce genre qu'on manque le rendez-vous avec des thèmes de recherches de pointe. Inversement, le Cnrs est totalement complice de mesures destinées à contraindre, sous peine de "mise au placard", des chercheurs confirmés à collaborer avec ces deux vaches malades, ces somptueux gâchis que sont les projets ITER et Megajoule.

Samedi juillet 6 heures, soit quatre jours après la mise en ligne sur le site de Researchgate, 546 connexions, 458 téléchargements de cet article. Du jamais vu sur Researchgate. Nous saurons lundi si des non-francophones ont téléchargé.

Ce même jour, nous avons enfin pu mettre la main sur un article de S.Antoci et D.E Liebscher, paru en 2001, il y a ... quinze ans, dans Astronomische Nachrischten, intitulé "Reconsidering Schwarzschild's original solution", qui va exactement dans le même sens que le nôtre. Bien que positionné dans la section gr-qc d'arXiv, où les Cosmic Men se tiennent mutuellement, et fébrilement au courant de leurs "avancées" et réflexions diverses, cet article ne semble pas avoir suscité d'échos. Le fait que notre travail ait plus d'impact vient du fait que nous l'avons (re)configuré de telle manière à ce qu'il touche plus de monde (avec des illustrations, des exemples en 2D).

Si des choses bougent ( et elles doivent bouger ) cela ne sera qu'en partant de "la base", de gens curieux et ouverts, qui interpelleront les stars de la discipline, lesquels ne répondent pour le moment à cet article que par un silence assourdissant.

D'autant plus que 2016 est "l"année Schwarzschild" et 2017 "le centenaire de l'invetion de la Relativité générale".

Il va falloir, en les citant, que nous reprenions le texte de :

                         L'article, mis en ligne sur Researchgate, téléchargeable à partir de mon site, moins quelques petites coquilles

Mise en ligne du 29 juin 2016 ( seconde partie de ce feuilleton, voir la première partie plus bas )

La situation est ... intéressante. L'article en question, tel que publié dans Modern Physics Letters A, est consacré à l'élimination de la singularité centrale dans la solution de Schwarzschild. Ce concept est à la base du modèle du trou noir. Or il semble bien que cette singularité centrale n'existe que dans l'imagination des black hole men. Prétendre cela équivaut à jeter aux orties des milliers de publications scientifiques et des centaines de thèses de doctorat. Comment est-ce possible ?

Ici, nous allons tous essayer de tirer cela au clair.

Dans les semaines passées j'ai fait des demandes de séminaires dans différentes directions. J'ai également écrit à une demi-douzaine de spécialistes en cosmologie et en ... géométrie.

Un seul m'a répondu, en me disant qu'il avait parcouru notre article rapidement, mais qu'étant donné que "toutes ces choses étaient établies de longue date, il était sceptique sur le fait que notre travail puisse apporter quelque chose de nouveau". Disons que cette page pourra entre autre constituer une réponse à son mail.

Je pense en effet que ça sera très dur d'amener des experts à simplement envisager que cette singularité centrale puisse ne pas exister. Rien qu'en lisant le litre de la publication, ou celui d'une proposition de séminaire, ils zapent. Certains se sont dit "Je ne vais pas répondre à une ânerie pareille", je pense.

Donc, si nous voulons que cette idée passe, il faut s'adresser à des gens qui n'ont rien à perdre dans l'opération : des étudiants, des ingénieurs, des gens ayant un minimum de bagage scientifique. En m'adressant à ceux-là je vais donc évoquer des concepts de base en géométrie différentielle. Au passage cela permettra à des gens ayant des connaissances de maths sup d'entrer de plein pied dans ce domaine réputé inabordable.

On commence par le concept de métrique, et on va l'illustrer avec un exemple, celui du tore. Nous allons envisager un déplacement élémentaires sur cette surface et calculer la longueur de ce déplacement. La figure ci-après suffit à situer le problème. En haut et à droite, la façon dont on repère le point sur le petit cercle "générateur".

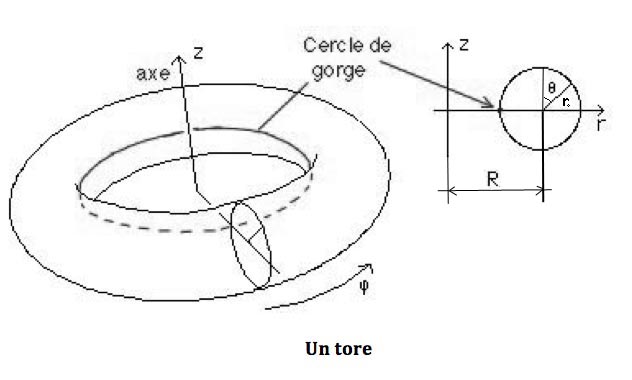
Trigonométrie plus Pytaghore nous donnent cet élément de longueur.

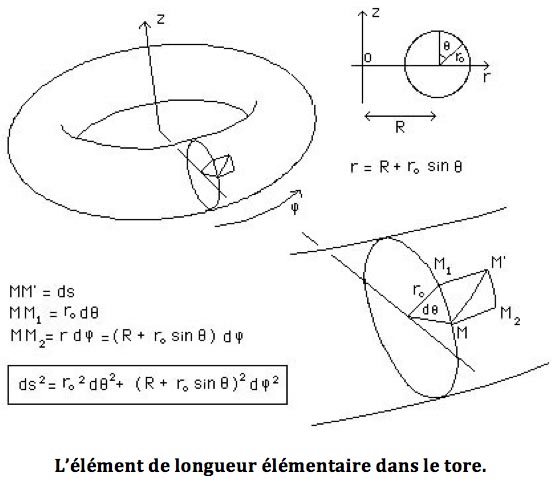
Cette expression encadrée est ce qu'on appelle la métrique du tore, ici exprimée à l'aide d'un jeu de coordonnées particulier et . Sans même utiliser le recours du dessin on peut y "lire" l'existence de deux familles de cercles particuliers, qui montrent que cette surface n'est pas "null homotopic", c'est à dire qu'on peut y tracer des courbes fermées dont une ne peut pas amener la longueur à zéro, l'homotopie étant une transformation où on déforme cette courbe de manière continue, en assurant la continuité de la tangente le long de ce contour fermé. Considérons les courbes correspondant à = constante. Ce sont des cercles, sur lesquels :

Ce sont les cercles générateurs du tore ( les petits cercles de la figure ci-dessus.

Considérons maintenant les coupes du tore correspondant à = constante. Dans la figure ci-dessus ceci conrrespondra à des cercles se situant dans des plans perpendiculaires à l'axe de symétrie du tore. Inutile de les dessiner pour les visualiser. Ils correspondront à :

ayant pour périmètre ( en n'opérant qu'un tour ) :

Ce qui imposera la contrainte :

Le plus petit cercle : on retrouve le cercle de gorge du tore. Le grand, c'est le cercle de jante.

Mathématiquement, une métrique peut s'exprimer dans une infinité de jeux de coordonnées. Nous allons passer d'une coordonnée à une coordonnée r (qui représentera la distance du point à l'axe de sympétrie du tore ). Il nous faut exprimer dans l'expression de la métrique ce changement de variable, en particulier à travers l'élément différentiel d

On extrait l'angle avec une fonction inverse, " l'arc sinus". Ca vous rappelle des souvenirs ? ....

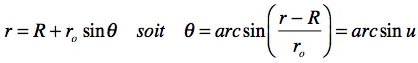
La métrique du tore est exprimée avec un premier jeu de coordonnées ( , ), mais il est évident qu'on peut l'exprimer dans n'importe lesquelles des coordonnées. Vous vous approchez ainsi, sans vous en rendre compte, d'un des concepts les plus pointus de la géométrie différentielle : la manipulation d'objets "coordinate invariant". Une métrique est l'un de ces objet.

Ainsi, tel Monsieur Jourdain, vous voilà en train de faire du calcul tensoriel sans vous en apercevoir. Mais je suis toujours partisan d'aborder les choses par le bas, en cherchant d'abord à quoi ça peut servir avant d'établir de puissantes généralités, en général opaques au premier coup d'oeil.

Dark Singularity

Donc, on va passe à des coordonnées ( r , ). Pour cela il faut différencier pour passer à une différentielle dr

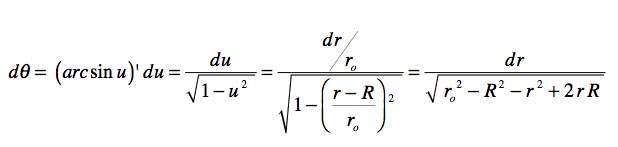
Pour ceux qui doivent dépoussiérer leurs connaissances, si la dérivée d'une fonction y = fx) est y' = dy/dx la dérivée de la fonction inverse x = g ( y ) c'est tout bêtement x' = dx/dy , donc l'inverse de la précédente. La dérivée du sinus, c'est le cosinus, qui est égal à la racine carre de 1 moins le sinus carré, c'est à dire de 1 - x carré. Vu ?

Vous suivez ? On continue ...

La métrique s'exprime alors comme ci-après. Mais elle se réfère au même objet.

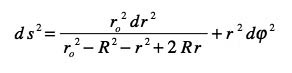
On a un dénominateur, qui s'annule pour :

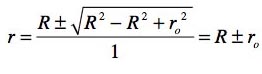
Un dénominateur qui s'annulle ? Cela nous fait apparaître deux "singularités" sous la forme de deux cercles correspondant à

Mais un tore ne présente aucune singularité ! Pour ceux qui n'ont jamais vu un tore, c'est comme une chambre à air de voiture, moins la valve.

Gilles d'Agostini, mon coworker depuis 20 ans, propose qu'on appelle cela une dark singularity, une "singularité sombre, ou ... noire".

Comme depuis des décennies on est dans la dark science jusqu'au cou, c'est pas mal. Eh oui, on nage dans la dark matter, la dark energy. On est plus à un dark machin près.

Signification de la modification de signature

Autre remarque : si le dénominateur est positif entre ces deux valeurs, il change de signe à l'extérieur. Or les signes des éléments de cette métrique constituent ce qu'on appelle sa signature. Donc dans la première formulation c'était ( + , + )

On voit alors qu'avec cet autre jeu de coordonnées, à l'intérieur des valeurs "critiques" la métrique est ( + , + ) alors qu'en dehors elle devient ( - , + )

Qu'est-ce que cela signifie ?

Envisageons des "trajectoires radiales" , en gardant phi constant. L'élément de longueur devient :

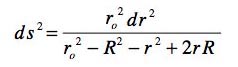
De toute évidence, à l'intérieur du domaine

le dénominateur est positif, mon élément de longueur est réel. Je suis bien dans la surface.

A l'extérieur l'élément de longueur devient imaginaire pur : je suis en dehors des clous, en dehors de la surface et la signature a changé.

Objet imaginaires, avez-vous donc une âme ?

En mathématique on peut écrire n'importe quoi, ça a toujours un sens, à condition de respecter un certain nombre de règles de syntaxe et de grammaire qui sont propres à ce language particulier. Car les mathématiques sont un language avec une structure hypothético-déductive. Une des richesses de mathématiques est qu'il arrive parfois qu'on manipule des éléments imprévus, qui obligent à étendre l'espace du discours. Imaginons qu'on se replace à l'époque, fictive, où on viendrait juste d'inventer l'arithmétique, l'algèbre et l'opérateur "chercher la racine carrée de" . Soudain quelqu'un se dirait "que se passe-t-il quand j'écris la racine carré d'un nombre négatif?". On aurait alors été dans l'obligation d'étendre l'algèbre aux nombres complexes et "racine de moins quelques chose" deviendrait alors un nombre imaginaire pur.

Si on définit un cercle par son équation x² + y² = 4 et qu'on envisage de chercher son intersection avec la droite x = 7, le calcul formel nous fournira bien deux valeurs de l'ordonnée correspondante y. Mais ces valeurs, plus ou moins racine de moins 45 seront imaginaires pures. On en déduira que cette droite ne coupe pas ce cercle.

Revenons à l'exemple ci-dessus où une formule nous permet de calculer un élément de longueur au voisinage d'un point supposé se trouver sur une surface, définie par sa métrique, par cette formule. En dehors du domaine ci-dessus, la longueur devient ... imaginaire. Pourrait-on dire qu'on se trouve "dans la partie imaginaire d'un tore" ?

Imaginez un garagiste fou qui a décidé de coller, sur une chambre à air, une rustine, en un point situé près de l'axe de la roue. Il y arrivera peut être, sur une chambre à air imaginaire, pas sur la chambre à air réelle, celle .... du physicien.

Après ce préambule, vous aurez envie de dire : "Mais que veut-il me montrer avec cet exemple ?"

C'est très facile de créer de la singularité là où il n'y en a pas

Donnons un exemple encore plus simple, en partant de la métrique de la sphère :

Prenons là encore la distance r à l'axe comme nouvelle variable :

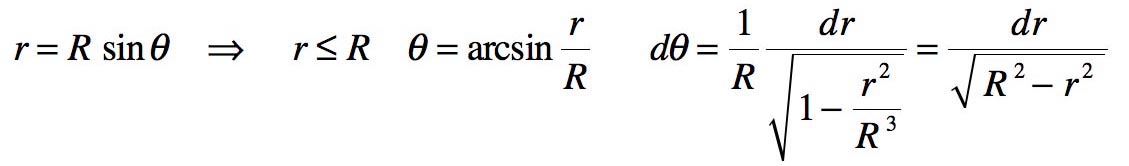
La métrique s'exprime alors sous la forme :

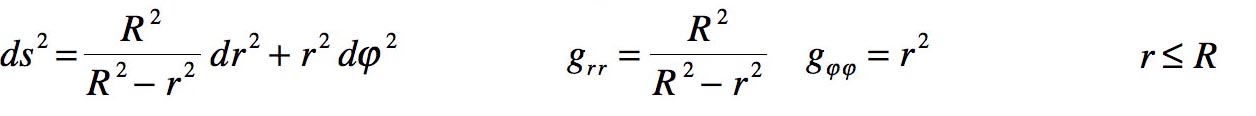
Encore une fois, on a créé une description de la sphère, pour r > R , qui ne correspond à rien de réel. En même temps on a un "lieu singulier", en r = R qui n'est qu'une coordinate singularity.

Au passage on remarquera que sous sa forme première cette métrique est telle que :

En ces points le déterminant de la métrique est nul. Pourtant les pôles d'une sphère ne sont pas des "true singularities".

Des objets géométriques définis par leur métrique

C'est tout le problème d'un objet géométrique défini par sa métrique. En principe celle-ci peut être définie en utilisant n'importe quel système de coordonnées. Mais, à quel jeu joue-t-on ? On fait de la physique ? On reste dans le réel, où on se donne le droit de s'ébattre dans une métaphysique imaginaire ? Il faut définir les règles du jeu.

La physique : c'est le choix du jeu de coordonnées, la façon de lire une solution mathématique

S'agissant de ce tore, pour lequel vous pouvez disposer d'un plongement isométrique dans R3 ( qui conserve les longueurs ) vous refuserez l'idée de manipuler des longueurs imaginaires pures, ou complexes. Enfin, au risque de paraître vieux jeu, le physicien que je suis s'y refuse.

Au risque de paraître vieux jeu, restons dans le réel.

Eh bien c'est pareil en physique. En Relativité Générale on manipule des métriques à tout vat. Ces métrique se réfèrent à un "objet géométrique", qui est indépendant des coordonnées qu'on prend pour le décrire, à condition de rester dans les clous, de ne pas avoir un élément de longueur imaginaire, de rester dans l'hypersurface.

Si vous obtenez une longueur imaginaire pure, ou que votre système de coordonnées vous fait apparaître dans certaines régions un changement de signature, avec comme corollaire une singularité quelque part, danger : vous sortez de l'hypersurface, vous disqualifié.

C'est ce que nous allons vous montrer dans ce qui va suivre, dans du 4D. Nous nous réfèrerons à l'article original de Karl Schwarzschild, publié en 1916.

Retour vers le papier original de Schwarzschild, 1916

Rappelons les faits : en 1915 Einstein publie aux Comptes Rendus de l'Académie des Sciences de Prusse un article qui deviendra célèbre, où il présente "l'équation d'Einstein". Il aurait été plus juste de l'appeler l'équation d'Einstein-Hilbert, mais passons ...

Molibilisé sur le front russe Karl Schwarzcshild trouve aussitôt la première solution de cette équation. C'est à la fois un grand physicien et un grand mathématicien. Il envoie ce travail à Einstein qui, entre temps, est devenu referee de cette revue. Celui-ci publie d'article. Sur cet article original, en allemand (Merci à Thiéry Pierre qui a mis la main sur un pdf fabriqué avec des scans de l'article original (combien l'ont lu ?) vous trouvez cette métrique, que tous ceux qui font de la cosmologie ont eu mille fois sous les yeux. Mais, chose bizarre, elle est exprimée avec une coordonnée R, et non r.

Encore plus bizarre, immédiatement à droite on trouve une relation permettant de passer de cette coordonnée R , désignée dans son article par Schwarzschild comme "un simple intermédiaire de calcul" à une coordonnée r . Au passage, la constante alpha, c'est le rayon de Schwarschild Rs ou 2m selon la façon dont on décide d'écrire cette constante.

Nous écrirons ce changement de variable introduit par Schwarzschild :

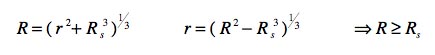
Lequel, c'est clair, impose que R soit plus grand que le rayon de Schwarzschild.

Voici la traduction de l'article en anglais, faite par deux Italiens. Vous pourrez vous repérer plus facilement. Dans cet article, dès sa deuxième page, Schwarzschild choisit une bête coordonnée radiale. On ne peut pas être plus clair. Et c'est cette coordonnée r qui figure dans l'expression du changement de variable liant R et r .

Fort bien, terminons le travail. Effectuons le changement de variable inverse pour exprimer cette solution métrique dans des coordonnées

( t , r , theta , phi ). Voyons ce que cela donne :

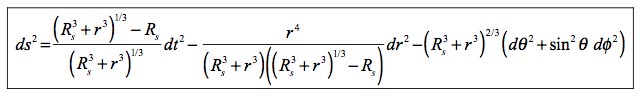
Diable, est-ce ... "la métrique de Petit" ???

Non, c'est tout simplement la métrique de Schwarzschild, l'expression de sa solution, dans les coordonnées qu'il avait choisies dès le départ.

Mais alors, pourquoi n'a-t-il pas fini son travail ? Parce que son but était de recoller avec le résultat de "Monsieur Einstein", ce qu'il dit à la fin de l'article. Celui-ci avait construit une solution (il restera à aller chercher son article original, vraisemblablement en allemand où il a consigné son travail). Schwarzschild ne fait qu'évoquer ce travail de "Monsieur Einstein" où celui-ci a effectivement trouvé l'avance du périhélie de Mercure, mais en utilisant une coordonnée R, qui semble être cet intermédiaire de calcul utilisé par Schwarzschild. Il faudra vérifier.

Si vous regardez la véritable expression de la solution de Karl Schwarzschild, encadrée, vous verrez que celle-ci est exempte de pathologies. Plus de dénominateurs qui tombent à zéro. La variable r peut tranquillement varier de zero à l'infini.

Au passage, pourquoi Schwarzschild n'a-t-il pas donné cette expression lui-même ?

Il n'en a pas eu le temps. Peu de temps après il a contracté dans les tranchées une affection qui l'a emporté quatre mois après.

Regardons cette métrique et envisageons sur cette hypersurface à 4 dimensions des trajectoires ( qui ne sont pas des géodésiques ) qui correspondraient à t et r constants. On a alors :

On reconnait, au signe près, la métrique d'une famille de sphères de rayon

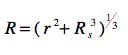
On aurait tendance immédiatement à qualifier ces sphères de "concentriques". C'est du à la façon dont, mentalement, nous engendrons les sphères, en tant que lieu des points se situant à égale distance d'un point fixe, ou centre. Mais il nous faut penser les choses autrement. En théorie des groupes on a un groupe O3, qui est le "groupe des rotations en 3 dimensions". Si on cherche les objets qui sont invariants par O3 on trouve ces sphères. Invariants, signifie que quand on "fait agir ce groupe" sur l'objet, celui-ci "se parcourt lui-même". Si on fait agir O3 sur une de ces sphères, elles resteront identiques à elles-mêmes.

O2, c'est l'équivalent à deux dimensions. Revenons au tore de tout à l'heure. On y avait trouvé une famille de cercles correspondant à = constante :

Ces cercles étaient invariants par l'action du groupe O2, un groupe que l'on imaginera ( dont on se fera une image ) en imaginant les rotations autour de l'axe de sympétrie du tore. Mais ces cercles "ne sont pas concentriques", au sens où il ne sont pas définis comme les lieux des points à égale distance d'un point fixe, leur "centre". Il faut les concevoir, les penser, les imaginer comme des objets invariants par l'action du groupe O2. C'est une géométrie construite à partir de la notion de groupe.

Ca nous parait évident de penser que cette famille de cercles inscrits sur le tore et situés dans "des plans horizontaux" ( une autre ... image ) ont un périmètre maximal et un périmètre minimal.

Mais il est beaucoup plus difficile d'imaginer que les sphères, liées à la métrique de Schwarzschild, puissent avoir une aire minimale qui correspond à la valeur R = R_s , quand r = 0 . Avec une dimension de plus, l'objet "contractile" n'est plus un lacet (une courbe fermée) mais une surface ayant la topologie de la sphère ( ici, tout simplement une sphère ). Et l'aire remplace le périmètre.

Un espace "null homotopic" 3D sera un espace où, partout, on pourra imaginer une surface fermée ayant la topologie de la sphère qui puisse se contracter ("par homotopie régulière") selon un point.

Le tore n'était pas "null homotopic" au sens où on trouvait des familles de cercles qui refusaient mordicus de se contracter selon un point, en restant bloqués au "cercle de gorge", de périmètre minimal.

Les mathématiciens ont des tas de mots compliqués pour dire tout cela, dont je préfère vous épargner la lecture.

Il nous faut alors imaginer que l'hypersurface de Schwarzschild, non null homotopic puisse correspondre à ce qu'on pourrait appeler une structure hypertorique possédant une structure faisant état d'une sphère de gorge (équivalent 3D du cercle de gorge du tore, objet 2D).

L'erreur qui a été faite, en 1916, en confondant la grandeur R introduite par Schwarzschild dans son article fondateur, pour lui simple intermédiaire de calcul, avec une distance radiale. Cette confusion traduit le fait qu'on a qualifié, sans le savoir, l'hypersurface de Schwarzschild de null-homotopy, propriété qu'elle ne ... possédait pas.

Pas plus de singularité que de beurre en broche ...

Mais, quand même, les coefficients de la métrique deviennent nuls quand r tend vers zéro. Serait-ce à dire que nous autions en r = 0 une singularité ?

Attention, ce r = 0 n'a rien à voir avec R = 0 ! Quand r = 0 on a R = Rs. Mais il faut quand même y aller voir.

D'après ce que je crois avoir compris on a une vraie singularité, une true singularity (et non une coordinate singularity, qui peut être éliminée par un changement de coordonnées, voir l'exemple du tore, ci-desssu) quand l'invariant de Kretchmann devient infini.

Dans la métrique de Schwarzschild le rayon de Schwarzschild ( sa constante alpha ) est :

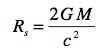
Le scalaire de Kretchmann est :

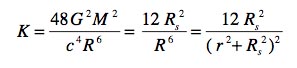
Il ne s'agit plus de l'évaluer quand R = 0 mais quand r = 0 , ce qui correspond à R = Rs . On trouve

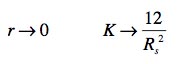
Une valeur tout à fait "paisible". J'en déduis que la solution de Schwarzschild, si exprimée dans "les bonnes coordonnées", est exempte de singularité.

Je pense que quand on envisage d'explorer "l'objet" pour des valeurs R < Rs on est simplement "hors hypersurface". D'où des tas de trucs qui deviennent imaginaires purs. Le "prolongement analytique de Kruskal" me semble être "une façon d'étudier la géométrie du tore au voisinage de son axe".

Au passage, je l'ai déjà dit, le fait de remplacer la métrique de Schwarzshild par celle de Kerr ( objet axisymétrique ) ne change rien au problème.Le cacul est plus compliqué mais le changement de variable fonctionne encore.

Mais alors, quid du changement de variable :

La métrique prend alors la forme (voir le détail du calcul plus loin dans la page ) :

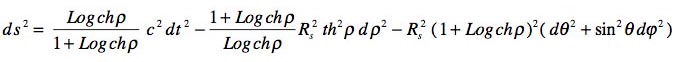
Là encore on peut considérer des trajetssur l'hypersurface correspondant à t et constants. Il vient :

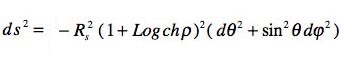
On reconnait la métrique d'une famille de sphères, d'aire :

Celles-ci ont une aire minimale, quand la variable   devient nulle. :

C'est l'aire de la sphère de gorge de cette 3-Hypersurface.

Respirez un grand coup. Ca va aller, vous verrez ...

Dans cette description en , dans cet espace de représentation, celle-ci peut prendre des valeurs négatives et alors l'aire des sphères se remet à croître, de même que le périmétre de la famille des cercle "horizontaux" ( c'est à dire invariants par action du groupe O2 ) se remet à croître quand on a passé le cercle de gorge.

Je sais que tout ceci est assez difficile à intégrer. Certains y parviendront facilement, d'autres, non. La vision dans l'espace n'est pas un talent partagé par tous ( il y a d'ailleurs des spécialistes en topologie qui ne voient absolument pas dans l'espace et pour lesquels la manipulation des objets géimétrique se limite à celle que mon épouse appelle " des crottes de mouches" ).

On pourrait faire une digression en étudiant l'objet défini par la métrique :

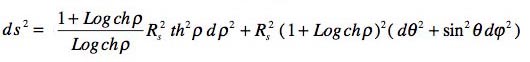
Exprimée à l'aide de la variable r selon le changement de variable "magique" :

ou, à travers son changement de variable inverse :

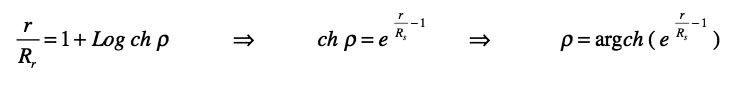
on retrouve alors la métrique du "diabolo 3D" avec cette variable r :

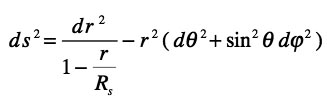
Voilà qui vous semble un peu plus familier. Et, en enlevant une autre dimensions on a la métrique du " Diabolo 2D " :

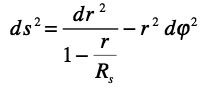
Dont on sait qu'elle définit une 2-surface qui se prête alors à un "plongement isométrique dans R3" ( conservant les longueurs ) :

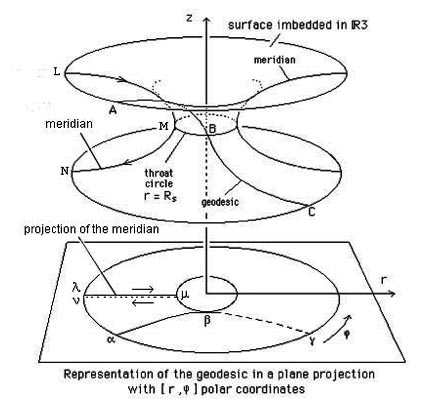
                                                                                              Diabolo 2D

On a montré ( dans l'article téléchargeable ) que cette surface était engendrée par la rotation d'une "parabole couché" autour de l'axe OZ.

Là, ça se dessine, on est rassuré, ça va. Il y a un "cercle de gorge". Plus difficile : passer au Diabolo 3D, qui a une sphère de gorge, et qui est proche parent de l'hypersurface de Schwarzschild, qui a aussi une sphère de gorge. Là, fini le dessin, rassurant.

Le fait que le déterminant de la métrique devienne nul en rho = 0 me semble être lié à l'inorientabilité de l'hypersurface en ce point. J'ai posé la question à un mathématicien-géomètre de l'université de Marseille. Pas encore de réponse; Ca me semble être une question importante.

En conclusion :

Nous n'avons fait que retourner à la publication originale de Schwarzschild. Si Schwarzschild avait désigné son "auxilliary quantity" par la lettre Z il n'y aurait jamais eu ce problème. Comment en est-on arrivé à considérer cet intermédiaire de calcul comme une coordonnée radiale ?

La réponse tient dans cette formule

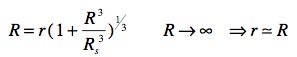
On voit "qu'à grande distance" ces deux grandeurs se rejoignent. Ainsi le calcul de l'avance du périhélie de Mercure donne le même résultat avec les deux variables. On peut penser qu'Einstein qui, de son propre aveu, n'était pas calé en maths, mais avait une intuition physique hors du commun, ne serait passé allé cherché plus loin. Et aucun de ses successeurs n'auraient remis en question les écrits du maître. C'est un peu vertigineux, mais ça n'est pas impossible.

Les experts diront : "vous amputez l'hypersurface d'une partie"

Nous, on pense qu'ils ont rajouté à l'hypersurface une portion ... imaginaire, qui n'a aucun sens physique.

Si nous avons raison, bonjour les dégâts. Exit les "théorèmes fondateurs sur la singularité"

Si nous avons raison, alors le "prolongement analytique" de Kruskal, qui permet d'examiner comment les choses se passent "à l'intérieur d'un trou noir" n'aura plus sa place dans les manuels de cosmologie (...).

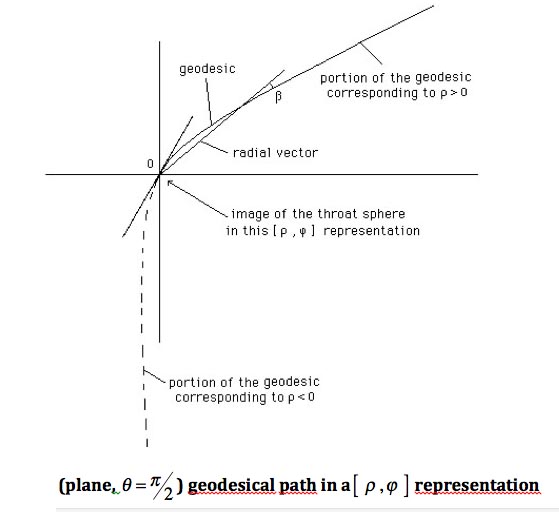
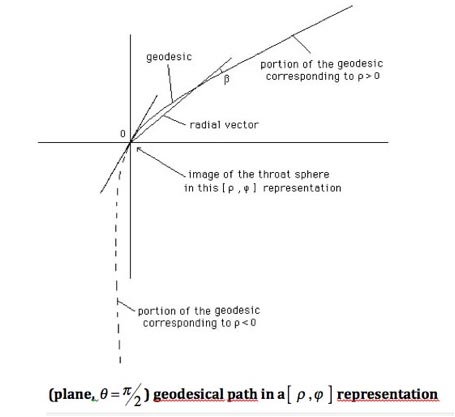
Si on opte pour la descripion en rho on doit alors s'interroger sur la signification de la portion de l'hypersurface (qui devient alors me semble-t-il un hypercone ) qui correspond à rho négatif. Géométriquement cet autre versant tend vers un espace de Minkowski, avec une métrique de Lorentz. Est-ce que ça correspondrait à l'intuition d'Hawking (avril 2016) qui disait que l'objet menait "vers un autre univers"?

Dans l'article que nous avons publié en 2015 on suggère que ce second versant est PT-symétrique. Il y a à la fois énantiomorphie et inversion de la coordonnée temps. Donc, théorème de Souriau, inversion de l'énerguie et de la masse. Ce "passage", quelle que soit la forme qu'on imagine lui donner (un simple point ou une "sphère de gorge" ) traduit une inversion de la masse.

                                                                                                                                              Affaire à suivre ...