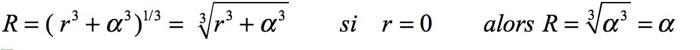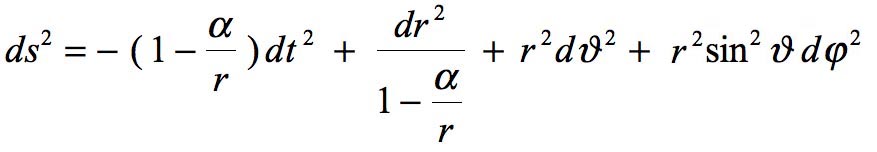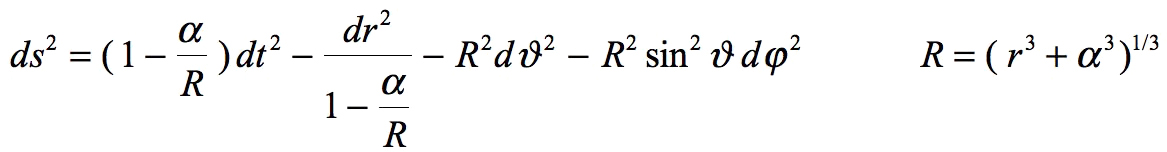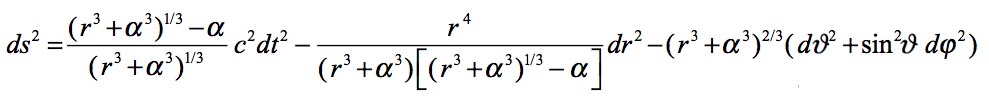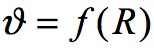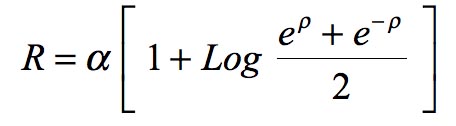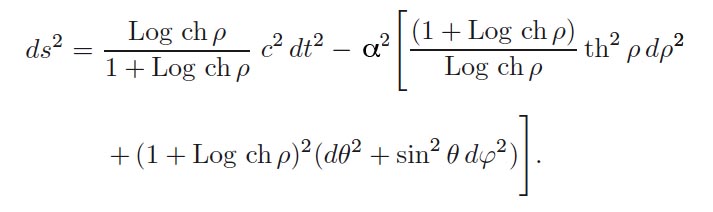Je rentre du colloque Karl Schwarzschild, qui s'est tenu en Allemagne au prestigieux FIAS, au Frankfurt Institute for Advanced Studies.
J'avais beaucoup hésité quand au contenu de mon poster et finalement décidé de présenter en gros mon système d'équations de champ couplées.
Un texte s'accordait mal avec le thème central du colloque, axé sur "la physique des trous noirs". C'est un sujet que je me proposais d'aborder, mais le papier que j'avais publié en 2015 dans Modern Physics Letters A : J.P.Petit & G.D’Agostini: Cancellation of the central singularity of the Schwarzschild solution with natural mass inversion process. Mo. Phys. Lett. A, vol. 30, n°9 (2015)
était ce qui se rapprochait le plus de ce thème. Comme il y avait un tableau noir à côté de mon poster, j'y ai donc écrit les grandes lignes de ce papier :
Ca a alors immédiatement attiré l'attention. Des congressistes ont pris des photos et un attroupement s'est formé. Un type d'une soixantaine d'années, un "senior researcher", a aussitôt exprimé son scepticisme quant au fait que tous les aspects singuliers de la solution métrique trouvée par Schwarzschild en 1916, et qui sert de support à la théorie du trou noir, puissent être éliminés à l'aide d'un unique changement de variable. Comme il n'était pas, comme d'autres, porteur d'un badge, j'en ai conclu qu'il devait faire partie du FIAS, du Frankfurt Institute for Advanced Science, hébergeant ce colloque. Voici ce changement de variable :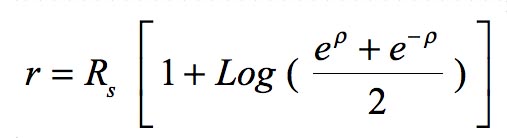 
Enfin, une critique ! Pour rendre les choses encore plus claires j'ai rapidement mis tous les détails du calcul sur une feuille que j'ai donnés à mon expert, et qu'il est allé consulter pendant un quart d'heure, assis sur une chaise.
Tout le monde a attendu son verdict. Il a fini par me rendre ma feuille avec un signe d'acquiescement, emprunt de la plus grande perplexité. Je pense qu'il a du se dire "je n'ai jamais vu ce truc nulle part. Il y a forcément une erreur que je ne vois pas. Mais je verrai ça plus tard. " J'ai essayé de le brancher sur ce problème, qui soulève la question de l'interprétation du résultat de Karl Schwarzschild en 1916 (le colloque s'intitulait "Colloque Karl Schwarzschild" !). Je lui ai demandé s'il avait lu l'article original publié aux annales de l'Académie des Sciences de Prusse : K.Schwarzschild: Über das Gravitational eines Massenpunkets nach der Einsteineschen Theory. Stizber. Preuss. Acada. Wiss. Berlin, p.189–196 (13 Jan.1916). English version by S.Antoci and A.Loinger at arXiv:physics/9905030 (12 May 1999) ainsi que le second article, publié quelques semaines plus tard, quelques mois seulement avant sa mort : K.Schwarzschild: Über das Gravitationsfeld einer Kugel aus incompressibler Flüssigkeit nach Einsteinsechen Theorie. Preuss. Acada. Wiss. Berlin, p.189–196 (24 feb.1916). English version by S.Antoci at arXiv:physics/9912033 (16 Dec. 1999) Il m'a avoué qu'il ne les avait jamais lus (...) en ajoutant: - Vous lisez l'allemand ? - Non, j'ai simplement eu accès à des traductions en anglais, relativement récentes, il est vrai (1999) pour des documents datant maintenant d'un siècle. J'ai ces documents sur mon portable. Voulez-vous que nous les examinions ensemble ? Il y a aussi un texte très important que David Hilbert a publié en décembre 1916 et où il reprend ce travail de Schwarzschild. D.Hilbert: "Die Grundlagen der Physik (Zweite Mitteilung)" Il a préféré éluder, en ajoutant qu'il ne connaissait pas non plus cet autre texte (...). En fait, ce que j'ai pu réaliser à Francfort c'est que les black hole men ne connaissent simplement pas les textes fondateurs à partir desquels ont été conçus les travaux qu'ils entendent développer. Lors d'un exposé magistral, devant l'ensemble des congressiste Juan Maldacenua, une "figure" des développements modernes de la théorie des trous noirs, a commencé par dire ( c'est reproduit dans la plaquette éditée pour le colloque )
Juan Maldacena - The Schwarzschild solution has confused us over a hundred years and it has forced us to sharpen our views on space and time. It has lead to sharper understanding of Einstein’s theory. Experimentally, it is explaining several astrophysical observations. Its quantum aspects have been a source of theoretical paradoxes that are forcing us to understand better the relation between spacetime geometry and quantum mechanics. Traduction : - La solution de Schwarzschild a été pendant un siècle une source de confusion et nous a contraint à approfondir la façon dont nous concevions l'espace et le temps. Ceci nous a amenés à une meilleure compréhension de la théorie d'Einstein. Sur le plan expérimental cela a expliqué un certain nombre d'observations. Les aspects quantiques ont fait émerger des paradoxes théoriques qui nous ont contraint d'avoir ne meilleure vision des relations entre la géométrie de l'espace-temps et la mécabnique quantique. Concrètement, cela donne quoi ? Il y a d'abord eu la "découverte" du "rayonnement de Hawking". En fait, tout cela repose sur l'idée d'un mariage entre entre Relativité Générale et Mécanique Quantique. Or on sait que ... cette union n'a jamais été consommée (la gravitation refuse mordicus de se laisser quantifier, ce qui déboucherait sur la description d'un graviton, particule de spin 2, toujours absent au rapport).
Nos modernes théoriciens ont fini par se convaincre que ce fantasme avait valeur de réalité. C'est en effet en invoquant un phénomène quantique au voisinage de l'horizon des trous noirs qu'Hawking "a montré" que ceux-ci pouvaient perdre de l'énergie, "rayonner". Cela a aussitôt donné naissance au "paradoxe de l'horizon cosmologique". En effet dans ces objet baptisé trous noirs toute structure serait censée disparaître, être broyée. Donc les trous noirs seraient "des machines à détruire l'information". Maldacena a alors exposé les progrès réalisés concernant la "thermodynamique des trous noirs". Il a en particulier rappelé "qu'on avait montré que l'entropie des trous noirs était proportionnelle à leur aire". Bref, depuis les dernières décennies toute l'attention des théoriciens s'est portée sur la façon dont on pourrait contourner ce paradoxe de l'information. Vous avez sans doute entendu parler d'un "firewall" et d'autres choses de ce genre. Dans ses derniers travaux, Maldacena invoque un nouveau "maître-mot" : "entanglement" ( "Intrication" ). Un concept issu de la mécanique quantique et du fameux paradoxe d'Einstein-Podowlski-Rosen ( paradoxe EPR ) que j'ai décrit dans ma vidéo JANUS 6 ( à 14' 04"). C'est dans cette cette expérience que les deux photons émis sont "entangled". Bref, selon Maldacena "l'entanglement" apporte toutes les résponses. Ca, plus une puncée de théorie des cordes. Ce discours constitue le nec plus ultra de la theorie en 2017. Les participants au colloque se sont évidemment référés aux vidéos JANUS (voir la liste PDF de leurs contenus). Grâce au travail énorme fourni par Julien Geffray, six vidéos étaient équipées de ce sous-titrage à l'ouverture du colloque, les JANUS 14 à JANUS 19. Et c'est là qu'on réalise que ce sous-titrage en bon anglais est quelque chose d'absolument indispensable. Impossible de fournir du médiocre : les internautes zapperaient aussitôt. Geffray, qui suit mes travaux depuis 20 ans, et maîtrise totalement la langue de Skhaespeare, était le seul à pouvoir assurer ce travail de sous-titrage, fort délicat, à raison de 3 jours de travail plein par vidéo. Ceci représentant 15.000 à 20.000 caractères par vidéo, avec un texte comprenant pas mal de jargon spécifique à traduire, la difficulté d'organiser visuellement et de caler ces sous-titres au dixième de seconde près, ainsi que la création de fiches pointant vers mes papiers et bandes dessinées. Je lui ai payé ces six premiers travaux 500 euros pièce. Donc 3000 euros pour le sous-titrage de ces six vidéos, que j'ai prélevé sur l'argent que les internautes m'avaient envoyé. En voyant l'impact sur les non-francophones j'ai réalisé que je devrais faire équiper les 19 vidéos de ces (bons) sous-titres en anglais. Nous avons renégocié le prix et convenu de 350 euros par vidéo. Faites le calcul. Six vidéos à 500 euros, plus treize à 350 euros : budget total : 7500 euros. Plus que ce qui sera affecté au financement de mes trois premières missions dans des colloques internationaux. Ajoutons que je continuerai à produire ces vidéos au rythme de deux par mois, soit 700 euros/mois (il y aura une vidéo Janus et la mécanique quantique). C'est à mon avis de l'argent bien placé car si les textes présents dans les sites internet finissent souvent dans l'oubli, il n'en est pas de même pour les vidéos, qui perdureront sans limitation de temps et qui sont l'outil de communication moderne par excellence. Budget prévisionnel, jusqu'au printemps 2018, sous-titrage et colloques : 17.000 euros Faire émerger la vérité a un prix Si l'argent envoyé par les internautes (un immense merci à eux!) suffit pour assurer ma présence dans les quelques colloques à venir (Francfort, puis Paris, COSMO 17 ... ) j'ai besoin d'une nouvelle aide supplémentaire, urgente, pour faire face à ces frais de sous-titrage. Impact de ces vidéos : des réactions de jeunes chercheurs dont l'un, un Italien, a fini par me dire : - J'ai vu vos papiers sur votre modèle Janus (il avait la compétence pour en apprécier le contenu). Je regarde comment vous êtes acceuilli ici. Comment pouvez-vous espérer que ces gens fassent autre chose que de vous tourner le dos ? Ce que vous amenez met à bas les bases mêmes de leurs travaux ! Le contact avec ce garçon a été établi et maintenu, qui travaille en Italie sur la loi de Newton modifiée. C'est une première graine plantée. Si je continue à "draguer dans les colloques internationaux", il y en aura d'autres, dans la jeune génération et probablement pas chez ceux qui auront établi leur notoriété sur les travaux fantasmatiques que j'ai évoqués. Des jeunes qui se diront "je ne crois qu'à moitié à cette loi de Newton modifiée. Et si j'essayais de voir où me mênent ces idées de ce Français ? ". Ces contacts et échanges seront facilités par le fait que ces jeunes chercheurs auront pu prendre connaissance des vidéos, puis des articles quand ils seront amenés à me rencontrer. A Francfort la plupart des articles étaient centrés sur "la physique des trous noirs", sur "ce que vous pourriez observer, si vous l'observiez...". En ajoutant à cela une nouvelle idée à la mode, celle d'un univers "holographique" (il faudra que je crée une vidéo pour expliquer aux internautes ce qu'est réellement un hologramme. Je crois que ça sera bienvenu). Une femme nous a expliqué "qu'il ne fallait pas avoir peur des cordes cosmiques". Un autre a montré comment des paires de mini-trous noirs pourraient se former pendant la phase inflationnaire de l'expansion cosmique. Ajoutons des histoires liées à la théorie des cordes, à des "collisions de branes". J'étais pratiquement le seul à me singulariser, en proposant des travaux et des résultat ... susceptibles d'être confrontés à des observations. Si je veux contraindre cette communauté scientifique, perdue dans ses rêves, à réagir, il faut que je m'en prenne à leur enfant chéri, le trou noir, ce que je ne comptais faire que beaucoup plus tard. Mais le climat du colloque de Francfort m'a amené à corriger mon tir, aussi le titre de la prochaine vidéo sera :
JANUS 21 : Le trou noir, né d'une mauvaise interprétation de la solution trouvée par Karl Schwarzschild en 1916
Et ça sera également le discours que je tiendrai au colloque COSMO 17, à Paris. Il ne s'agira pas pour le moment de proposer un modèle alternatif, mais de dire : - Tel quel, ce modèle de cet objet que vous appelez trou noir est inconsistant, il ne correspond pas à la solution trouvée par Schwarzschild en 1916 et je le montre.
Le mathématicien Karl Schwarzschild, La solution trouvée par en 1916 par Karl Schwarzschild est :
Dans cet article il définit parfaitement une coordonnée r comme était une "coordonnée polaire" :
Mais il introduit ce qu'il nomme un quantité auxiliaire R , et c'est à travers elle qu'il exprime sa célèbre solution de janvier 1916 : Il décède à Potsdam le 11 mai 1916 à 43 ans trois mois après sa publication de janvier 1916
Point n'est besoin d'être un crack en mathématiques pour voir que, dans mesure où le r choisi par Schwarzschild (il le définit plus haut) est strictement positif, cette grandeur intermédiaire R n'est pas libre mais a une limite inférieure qui est alpha :
En reprenant ce travail, dans un article de décembre 1916 l'immense mathématicien Allemand
David Hilbert, 54 ans en 1916 juge inintéressant cette façon d'exprimer la solution qui, dans ce cas, selo lui, "ne fait que renvoyer la singularité ( en R = alpha ) à l'origine, en r = 0 ". Il exprime cette "opinion personnelle", dans son article du 23 décembre 1916 (Schwarzschild en mort en mai) :
En fait, Hilbert travaillait déjà très activement à cet article depuis des années, le titre signifiant "Fondements de la Physique" (!...). On a tendance à imaginer qu'Einstein était le physicien et Hilbert le pur mathématicien. Effectivement on cite souvent une anedote qui rapporte qu'un jour Hilbert avait été sollicité pour remplacer son collègue mathématicien Felix Klein, lequel donnait chaque année une conférence aux élèves ingénieurs d'une école. Hilbert commença alors son exposé par une boutade : - On dit que les mathématiciens et les physiciens ont du mal à communiquer. En fait, ce n'est pas vrai. Il n'ont simplement rien à faire ensemble! L'oeuvre de Hilbert, en mathématique, est effectivement considérable, monumentale. Mais si on a la curiosité de se réferer à ce document, on y découvrira qu'il tente de poser les bases d'une physique hautement mathématisée ( une "physique mathématique" en fait). Cela signifie qu'Hilbert, par rapport à sa phrase, lors de cette conférence donnée dans cette école d'ingénieurs, a changé totalement d'optique, peut-être suite à sa rencontre avec Einstein, ou plus généralement suite à des échanges avec les grands physiciens de l'époque. Bien sûr, s'agissant d'apporter alors sa propre contribution, il voit grand, immédiatement. Ce Grand Seigneur de la science ne saurait théoriser au ras des pâquerettes, traiter de quelque problèmes subsidiaires. Ce papier pose donc les base d'une "approche Lagrangienne" de toute la physique, c'est à dire à la fois la gravitation et l'électromagnétisme. Dans cet écrit il est clair qu'Hilbert ambitionne de regrouper dans cette approche "toute la physique de l'époque" dans ce qu'on appellera plus tard une "théorie des champs unifiés", un travail qu'Einstein tentera vainement de mener à bien jusqu'à la fin de sa vie. L'entreprise échoua, parce qu'on ne peut pas inclure ces deux formalismes dans seulement quatre dimensions, comme montré par Souriau en 1954 (dans le chapitre VII de son ouvrage "Geométrie et Relativité, édition Hermann" ). Il en faut ... cinq, une de plus : la "dimension de Kaluza". Quand Hilbert publie ce papier de 22 pages, le 23 décembre 1916, il ne s'agit nullement d'une improvisation faisant suite aux papiers de janvier et de février 1916 de Schwarzschild. C'est en fait l'article qu'il avait présenté en novembre 1915 (puis retiré, ne l'estimant pas assez construit), agrémenté de différents développements, dont cette solution non-linéaire de l'équation de champ, en mentionnant au passage que Schwarzschild l'avait déjà produite. Le fait que Schwarzschild ait produit en janvier cette solution n'est, pour lui, qu'un point de détail dans la vaste freque qu'il présente. Il était au courant du décès de Schwarzschild, qu'Einstein avait annoncé à l'Académie des Sciences de Prusse le 18 juin 1916. Disons que, de la part de Hilbert, comme orsaison funêbre, c'est évidemment assez succinct. Tout est dans l'extrait suivant :
Il introduit quatre coordonnées, w1, w2, w3, w4 et il précisé aussitôt que les trois premières, les coordonnées d'espace, peuvent s'exprimer comme il le fait, à l'aide de coordonnées polaires. Dans la mesure où il estime que ce problème, du champ gravitationnel autour d'un point-masse relève d'une "symétrie centrale" (zentrischsymmetrisch), cela lui parait aller de soi.
Dans la dernière ligne il pousse même les choses plus loin, en écrivant que son terme G(r) est identifié au carré de cette "distance radiale". Alors tout s'enchaîne et des générations de scientifiques reproduiront cette approche dans des centaines d'ouvrages. Au passage voici comment il gère cette variable temps l.
Chez Hilbert le temps est une grandeur imaginaire pure ! C'est son interprétation de la Relativité.
Dans cette équation (45) il ne fait figurer que la "forme bilinéaire" mais nous découvrons l'origine de ce choix d'une signature de la métrique qui est ( + + + - ).
Cette écriture concentre l'attention sur la partie réelle, tangible, de l'espace-temps, l'espace, affecté de trois signes plus. Le temps , lui, est imaginaire. Donc, au carré, cela donne un signe moins. Au passage l'élément de longueur s le devient aussi, de même que ce qu'on appelle "le temps propre". Normal : pour Hilbert, tout ce qui relève du temps doit être imaginaire : Il dit qu'il retrouve alors, modulo l'inversion des signes, le résultat de Schwarzschild, qui devrait alors s'écrire :
Pourtant, il y a une différence. Chez Schwarzschild ceci ne s'écrit pas avec la lettre r mais avec une lettre R.
C'est très différent. Mais Hilbert ne s'attache pas à ce détail, vu que dans les conditions usuelles de l'astronomie r est toujours grand devant alpha ( grandeur qu'on appelera plus tard "rayon de Schwarzcshild" ) . Pour faire apparaître cette différence, explicitons cette solution, comme aurait pu le faire Schwarzschild lui-même. Nous obtenons :
Mais il ne l'a pas fait parce que l'écriture précédente lui paraissait suffire. Cette métrique est régulière pour toute valeur de la variable r supérieure à zéro. Quand cette variable devient nulle les coefficients des deux premiers termes deviennent nuls. On verra plus loin l'interprétation de ce point. Le seul commentaire de Hilbert se résume à une courte note de bas de page :
Traduction : - Le fait de transporter le lieu où r = alpha à l'origine, comme le fait Schwarzschild, n'est pas, selon ma propre opinion, quelque chose à recommander. Par ailleurs cette transformation de Schwarzschild n'est pas la plus simple pour arriver à un tel résultat.
Ce lieu r = alpha était pour Hilbert, au moment où a écrit ce papier une singularité "une true singularity", ou "singularité vraie" . Or on a montré par la suite que c'était une "coordinate singularity", qui pouvait être éliminée par un changement de variable. On sait que ces solutions métriques peuvent s'exprimer dans n'importe quel choix de jeu de coordonnées. C'est une propriété fondamentale des solutions de cette équation de champ. Le choix de tel ou tel type de jeu est un geste de physicien. Cela consiste à donner une interprètation physique à ces coordonnées. Reste alors à confronter ces résultats théoriques à l'observation, c'est à dire à calculer les trajectoires géodésiques des points masses orbitant dans le champ créé par ce "point-masse". C'est ce qu'ils ont tous fait. Classiquement, on assimile la variable R à une coordonnée polaire, qui serait donc susceptible de s'annuler. On montre que ces trajectoires géodésiques s'inscrivent dans des plans. On peut alors exprimer la solution sous forme d'une fonction
et en comparant les courbes obtenues avec les données d'observation, on arrive à la conclusion : - Ces trajectoires sont des "quasi-côniques" dont l'un des foyers se situe en R = 0 . - Dans les conditions usuelles de l'astronomie planétaire les trajectoires elliptiques sont très proches d'ellipses, l'écart représentant ce qu'on appelle "l'avance du périhélie". On remarquera que quand R >> alpha les grandeurs r et R sont pratiquement identiques. Schwarzschild en fait la remarque dans son papier : Mais c'est plus lisible dans la version anglaise :
Ainsi, si on excepte le choix d'une autre signature, on peut dire que les solutions de Schwarzschild et de Hilbert ( ainsi que la solution linéarisé proposée par Einstein dès 1915 ) se rejoignent, conduisent à des résultats pratiquement identiques, s'agissant d'astronomie planétaire. Donc, qu'on opte pour la variable radiale r de Hilbert ou de R pour Schwarzschild, les résultats théoriques collent avec "le réel". Le rayon de cette sphère qu'est le Soleil est de 700.000 kilomètres. Comme le calcule aussitôt Schwarzschild, sa grandeur alpha (le "Rayon de Scghwarzschild" ) est de 3 kilomètres. Confondre cette sphère avec un point ne représente qu'une erreur de quatre millionièmes. Il faut aussi mentionner, mais cela je le détaillerai dans une prochaine vidéo, que Schwarzschild, non content de fournir cette solution "extérieur" avait aussi construit "la solution intérieure" ( décrivant la géométrie à l'intérieur d'une sphère de densité constante ). K.Schwarzschild: Über das Gravitationsfeld einer Kugel aus incompressibler Flüssigkeit nach Einsteinsechen Theorie. Preuss. Acada. Wiss. Berlin, p.189-196 (24 feb.1916). Voici la traduction en anglaise de ce second papier, de février 1916 (un mois après !). Il avait aussi remarqué que, pour le Soleil alpha (c'est à dire ce qu'on appelera par la suite "le rayon de Schwarzschild", de l'ordre de 3 km, était situé très à l'intérieur de l'astre. Ca n'est qu'aujourd'hui, avec des objets comme les étoiles à neutrons, qu'on se pose le problème de la représentation géométrique et physique d'objets où "la variable distance" n'est plus du tout négligeable devant ce rayon de Schwarzcschild. Mais alors, quelle variable doit-on choisir ? Cette de Hilbert ou celle de Schwarzschild. Les théoriciens ont alors proposé de conférer un caractère physique à cette solution extérieure et ont dit qu'elle décrivait un objet qu'ils ont appelé "trou noir". Géométriquement il faut alors produire une réponse : - Dans la représentation se Schwarzschild, pour ce qui se passe en r = 0 - Dans la représentation de Hilbert, pour ce qui se passe en R < alpha ( considéré comme "l'intérieur du trou noir" ) On notera que cette question ne se pose pas, dans la représentation de Schwarzschild. Il n'est pas nécessaire de se demander ce qui se passe quand les points-masse tombent " à l'intérieur", puisque ce intérieur ... n'existe pas. Par contre, dans la représentation de Hilbert, si on confère quelque réalité à cet "intérieur", celui-ci est bien étrange. La signature de la métrique est altérée, ce qui fait dire à nos théoriciens "cela signifie qu'à l'intérieur r devient le temps et t le rayon". Dans un article de 2015 : J.P.Petit & G.D’Agostini: Cancellation of the central singularity of the Schwarzschild solution with natural mass inversion process. Mo. Phys. Lett. A, vol. 30, n°9 (2015) j'ai indiqué un autre choix de coordonnées, dérivant de la solution de Schwarzschild à travers le changement de variable :
qui conduit à une présentation de la solution métrique sous la forme :
Elle est alors régulière quelles que soient les valeurs des variables, si on excepte le fait que le premier terme est nul à l'origine, ce qui entraîne automatiquement la nullité du déterminant ce cette métrique. On interprète alors la géométrie afférente en considérant que cette métrique décrit un passage reliant deux espaces de Minkowski PT-symétriques, la jonction s'effectuant à travers une sphère de gorge, de périmètre 2 pi alpha . Le long de cette sphère le déterminant est nul, ce qui traduit, le long de cette sphère, la double inversion de la flèche du temps et de l'espace lors de la traversée de cette surface. Quand on considère la géométrie de Schwarzschild, solution de l'équation de champ, exprimée dans les coordonnées La propriété de symétrie sphérique de la solution fait qu'on peut envisager de fixer trois des quatre coordonnées et envisager un tour de 2 pi selon la coordonnée théta. La sphère de gorge, dans la représentation de Hilbert, correspond à R = alpha. Si on fait t = constante, phi = constante et qu'on effectue ce tour selon théta, on trouvea pour résultat 2 pi alpha, la longueur mesurée sur un grand cercle de la sphère de gorge. Rééditons cette opération dans ma représentation Ce qui est plus surprenant c'est qu'en optant pour la représentation de Schwarzschild C'est très déroutant, car "en tournant autour du point r = 0 " on obtient une longueur non nulle ! Donc ... ça n'est pas un point ! C'est l'aspect extrêmement déconcertant de cette géométrie différentielle et de cette représentation d'objet par leurs métriques. Cette expérience vous fait simplement comprendre que vous devez cesser d'attribuer un caractère "dimensionnel" à cette lettre r. C'est justement en l'imaginant comme "une distance radiale" que les confusions se produisent. On l'aurait appelé " béta" ça aurait tout arrangé. En fait c'est le mot "dimension" qui est générateur d'erreur. Au lieu de dire "nous allons repérer les points dans cet objet géométrique avec un ensemble de dimensions" on devrait dire - Nous allons repérer les points dans cet objet géométrique à l'aide des marqueurs d'espace :
Mais cette lettre x est encore trompeuse. Elle ne gènera nullement un mathématicien qui y verra un simple nombre ou un angle. Pour éviter de voir apparaître des idées fausses comme celle selon laquelle l'objet correspondant à r = 0 serait un point, mieux vaudrait écrire par exemple :
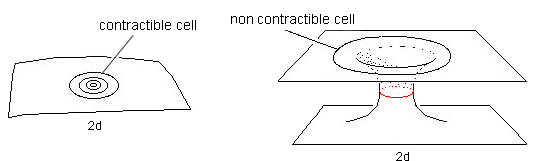
Revenons à ce concept général de métrique En mathématiques, en géométrie, comment apparaît ce concept ? La Terre n'est pas plane. C'est une sphère. Cela pose des problèmes aux cartographes. Si on figure ses continents sur une mappemonde, ça va. Mais comment faire si on ne dispose que de feuilles de papier, de supports plans, comment procéder? On constituera alors un ensemble de cartes constituant un atlas. Des cartes voisines peuvent être reliées entre elles en ajustant la correspondance entre méridiens et parallèles. Plus généralement on peut ainsi cartographier n'importe quelle surface. La carrosserie d'une voiture, par exemple. Chaque élément plan de cet atlas correspond à une description métrique locale. Les mathématiciens-géomètres ont étendu ce concept en envisageant de considérer des Atlas constitués d'éléments non-euclidiens. Imaginez une planète ou le papier n'existe pas et où les hommes disposeraient de supports sous la forme de feuilles séchées, affectant la forme de portions de sphère, qui peuvent être empilées les unes sur les autres en constituant un étrange "atlas", courbe. Là encore, une telle technique permettrait de cartographier n'importe quoi, de proche en proche (y compris un plan!) On remarquera que cette technique n'induit aucune contrainte Le simple fait d'envisager de décrire l'objet liés à la métrique de Schwarzschild à l'aide de "coordonnées polaires" représente, implicitement, une hypothèse forte sur sa topologie. Dans ce qui suivra on suivra l'idée selon laquelle cette solution métrique recèle sa propre topologie et qu'on n'est pas libre de choisir celle-ci. On sort alors complètement de cette approche classique des cartes constituant un atlas, en imaginant que l'objet ne doit être décrit que par sa métrique, exprimée dans un jeu de coordonnées ( "qui va bien" ) c'est à dire qui est en accord avec la topologie implicitement liée à cette solution métrique. Le fil conducteur étant : - L'élément de longueur s doit être réel partout - Et son corollaire : la signature de la métrique est un invariant. Sur la base de ces remarques et suggestions on peut alors mettre en doute le modèle du trou noir et ses multiples pathologies. Ne serait-il pas plutôt la conséquence de la façon dont Hilbert a interprété cette géométrie, qui a créé cette chimère qu'on désigne comme : "l'intérieur du trou noir", auquel on accède grâce au "prolongement analytique de Kruskal" a propos duquel Maldacena, dans sa conférence, a dit "que cela permettait d'étendre la solution à tout l'espace-temps". Maldacena, et tous les autres, ont un a priori topologique, concernant l'objet d'étude. Comment cela se concrétise-t-il ? Topologiquement, considérons une surface 2D. Traçons une courbe fermée, puis tentons de réduire le périmètre de cette courbe à zéro. Il y a deux cas de figure. - Soit ce périmètre peut être amené à zéro - Soit on tombe sur une valeur minimale Ceci peut être illustré par le dessin ci-après :
A un être qui habiterait une telle surface, et qui poserait la question : - Qu'y a-t-il au centre de ce cercle ? On ne pourrait que répondre que sa question est dénuée de sens et que ces cercles-là n'ont pas de centre Si on passe à un monde à trois dimensions, cette contractibilité se traduirait par la possibilité de déformer une sphère en amenant son aire à zéro :
Si cette opération peut être menée à bien, alors cette sphère possède un "intérieur" et "un centre". Mais un espace 3D n'est pas automatiquement contractile. S'il ne l'est pas, alors dans une région la surface ayant la topologie d'une sphère S2, en feuiullant cet espace à l'aide de sphère voisines on verra l'aire de celles-ci passer par un minimum. Puis si on tente de poursuivre un tel feuilletage on verra cette aire s'accroître, l'aire minimale correspondant à celle d'une sphère de gorge. Il n'est plus possible de dessiner une telle chose, mais en se reportant à la figure précédente on verra qu'à droite un butte sur un cercle de gorge. Tout cela peut être étendu à une hypersurface 3D et à une hypersurface dotée d'un nombre quelconque de dimensions. En saluant le travail de Kruskal "ayant permis d'étendre la solution à tout l'espace temps" Maldacena ne se rend pas compte (comme des milliers d'autres avant lui) qu'il met en oeuvre, sans en être conscient, une hypothèse sur la topologie de l'hypersurface 4D dont il parle, "l'espace-temps". Or le fait que cette tentative se solde par l'altération de la signature de la métrique, allant de pair avec la transformation de l'éléments de longueur en une grandeur imaginaire pure. Ceci traduit simplement la "réponse" que fournit le formalisme : - Attention, vous êtes en dehors de l'hypersurface ! En fait il a voulu explorer une portion d'espace-temps qui n'existe pas, un peu comme un géomètre qui construirait un prolongement analytique pour étudier les propriétés du plan tangent à un tore ... près de son axe, ou comme un garagiste fou qui, dans le monde d'Alice au Pays des Merveilles s'efforcerait de coller une rustine sur la chambre à air d'une voiture dans une région située près de l'axe de la roue.
Si j'ai raison, alors que de papier, d'encre et de matière grise, y compris de matière grise quantique, consommés pour décrire un objet qui n'existe pas, et tout ce qu'il implique, comme les propriétés d'une "singularité centrale" ! On peut se demander pourquoi tout cela est apparemment passé complètement inaperçu depuis un siècle. Les historiens des sciences nous fourniront la réponse. Disons qu'avec son fantasme de temps imaginaire, Hilbert a fait passer l'idée d'une signature ( - + + + ) ce qui fait que, peut être, personne ne s'est plus tard soucié du fait que le carré de l'élément de longueur changeait de signe. Il est faux de dire "que ça n'est qu'une question de conventions". Pourtant Schwarzschild ( et Einstein ) avaient opté pour une signature ( + - - - ), témoin cet extrait du papier de Schwarzchild :
Inversement, en fixant le signe des termes se référant aux angles Hilbert, implicitement, verrouille une signature ( - + + + )
Les scientifiques, les étudiants et les ingénieurs qui voudront approfondir ces questions pourront télécharger les traductions anglaises des différents articles cités, qui n'ont probablement jamais été lus par nos modernes black hole men, lesquels semblent avoit perdu tout contact avec les réalités, construisant une astrophysique sans observation, issue d'une mathématique sans rigueur. La traduction en anglais du papier de Schwarzschild de janvier 1916 La traduction en anglais du papier de Schwarzschild de février 1916 La version traduite en anglais du papier de Hilbert de décembre 1916 Voir aussi le papier de S. Antoci ( 2003 ) "David Hilbert and the origin of Schwarzschild solution" |
Voir aussi les vidéos JANUS : Playlist YouTube complète et liste de leur contenus détaillés en PDF. |
on serait tenté de penser "que la sphère de gorge est alors réduite à un "point", "le point r = 0" . Ce serait attribuer à cette lettre r une vertu "dimensionnelle", alors qu'en géométrie différentielle les lettres décrivant les coordonnées ne sont que des "space markers" des "marqueurs d'espace", de simples nombres permettant de répérer des points. Les seules distances, longueurs qui aient un sens sont celles qu'on calculera avec la métrique et ces longueursdésignées par la lettre s sont invariantes quel que soit le système de coordonnées choisi, si on considère évidemment des chemins identiques, mais décrits par des coordonnées différentes; 
. La sphère de gorge correspond alors à rho = 0 . Le tour selon la coordonnée théta redonne la valeur 2 pi alpha.
