
13) Isometry groups.
Call a
a 3d rotation matrix. Write :
(78)

The SO3
x R group's element can be figured by the matrix :
(79)

which is
the product of two matrixes. The first :
(80)

belongs to SO3.
and the
second :
(81)

belongs
to the R time-translation group. Introduce
P and T symetries. We get a four components group, whose element is :
(82)

It is the
product of two matrixes :
(83)

and :
(84)

Let us
call this second sub group E1 (one-dimenional Euclid's group).
In the [ t , r , q
, j ] representation the isometry group is O3 x
E1
Let us return to the expression
of line-element in the [t , r ,q, j] coordinate system
:
(85)
...Classically, one considers that the associated isometry group is SO3 x R , which is not the largest one. It is O3 x E1, for the line-element is also invariant under space and time inversions.
Now, consider
the line element expresed into the "extended Eddington" form
(86)

that
we write :
(87)
![]()
Introducing
cartesian space-coordinates [ x1, x2, x3] :
(88)
![]()
(89)
![]()
(90)
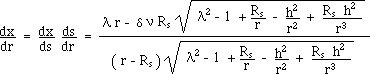
Then the
line element can be expressed in terms of [x ,x1,x2,x3] coordinates.
(91)

Now we search the isometric group of the metric, as expressed is this peculiar
coordinate system.
We first have P-symmetry.
The line element is invariant under :
(92)
x1 ® - x1
x2 ® - x2
x3 ® - x3
It is also
invariant through the change :
(93)
x ® - x
d ® - d
And through time-translations : x = x + e. It corresponds to the following four components group :

Its element
is the product of two matrixes. The first set
(94)

corresponds
to O3 and the second
forms a second sub group whose element is :
(95)

Call this second sub-group " TF ".
Then the isometry group of (86) is :
O3 x TF
Consider
now the Schwarzschild's metric expressed in [t = x/c
, r , q , j ] coordinate system. We can group the
two expressions (76) and (77) into :
(96)

Remember that d = -1 takes in charge the half space-time r > 0 while d = +1 takes in charge the second half space-time r < 0 , if we consider that the "black hole" is located in our fold, and the "white foutain" in the "twin fold".
If the situation is reversed, i.e. if the "black hole" is located in the twin fold, and the "white foutain" in ours, we get :
d = +1 takes in charge the half space-time r > 0
d = -1 takes in charge the half space-time r < 0
Consider
the first case (the "black hole" is in ours universe and the "white
foutain" is in the twin fold). There, the metric is :
(97)

Changing :
r ® -r
t ® -t
d ® -d
we get
the second metric :
(98)

Notice that the nullity of the determinant when r = 0 would corresponds to the local inversion of space (enantiomorphy) and time-coordinate at the point ( r = 0 ). In effect we need a non-zero determinant to define gaussian coordinates. See reference [1] 2.4
If the determinant is non zero, it makes possible to define a series of hypersurfaces( x° or x, or t = constant) (corresponding to a constant value of the chosen chronological marker), orthogonal to the geodesic x° or x or t coordinate lines ("world-lines" for "steady points").

Fig.15 : After fig. 2.1 of reference [1]
We could
express (97) and (98) in cartesian coordinates, as before, and refind (92) and
(93). The isometry group of (96) becomes :
(99)

The two half space-time folds are PT-symmetric.
Remeber Andrei Sakharov was the first, in 1967 (references [26] to [30]) to suggest that une Universe could be composed by two twin Universes, ours and a twin one, with "opposite times". Later he suggested that the twin fold could be enantiomorphic.
14) The phyical meaning of the inversion of cosmic time t.
This time-inversion is puzzling. It means that the time marker t is inversed when one follows a geodesic, from or fold to the twin one. Does it means that the clock of a "passenger", passing through this hypertoric bridge would be reversed ?
Above, we said that a couple "black hole - white foutain" could exist, where the "black hole" would be located in the twin fold and the "white foutain" in the other. It would mean that this "test passenger" could dive into the first hypertoric bridge and rise out from the second one. Could he come back at his space starting point and "kill his father" ?

Fig.16 : A (schematic) paradoxical journey.
The answer is no, for the sign of the elementary increment ds of his proper time does not change, along the geodesic he follows. So, what is the physical meaning of t ? None. It is just a coordinate.
Only proper time has a physical meaning.
So, what is the consequence of the inversion of this time-coordinate ?
We
must study the coadjoint action of the group on its space momentum (references
[11] and [12]). The element of the group is
(100)

This is a two components group ( m = ± 1 ), whose dimension is 4.
The inverse
matrix is :
(101)

Compute
the Lie algebra element. Write :
(102)
d a = w d e = e

Let us
compute : dg' = g-1 x
dg x
g
(103)

(104)
![]()
In order
to compute the coadjoint action (see ref. [11] ), introduce the scalar :
(105)
![]()
whose invariance
is ensured if :
(106)
![]()
i.e. :
(107)
![]()
The identification
provides the coadjoint action of the group ont its four components momentum
:
(108)
( l , m )
Remember
the number of momentum's components is equal to the group's dimension.
(109)
![]()
(110)
m' = m m
We can identify m to the mass (or to the energy E = mc2, indifferently).(110)
means that when a particle passes through the "throat sphere" its
mass is inversed (m' = -m). This is not surprinzing and gives the very physical
meaning of this "inversion of the time-coordinate".
... Following J.M.Souriau [12] we may call the
(m = +1) component of the group the "orthochron
ones", and (m = -1) the "antichron component".
The elements of the antichron component reverse the mass. Time-symmetry is equivalent
to m-symmetry, as shown by J.M.Souriau ( [12] p.197, chapter time and space
inversions).
15) Subsequent coupled field equations.
We started
from a single zero second member field equation :
(111)
S = 0
which was
supposed to come from a complete (Einstein's) equation :
(112)
S = c T
applying to vacuum (T=0). We may assume that the complete geometry may be described by two "conjugated metrics" g and g*, from which we can build two Einstein's geometric tensors S and S*. See references [13] to [15].
If the
two half space-times are empty, the set ( g , g*) is solution
of the system :
(113)
S = 0
(114)
S* = 0
(A steady
exact solution of the system (113) and (114) is given in reference [16]). Now
we can fill the first space time fold by positive mass (positive energy and
pressure) corresponding to a tensor field T and the second one by negative
mass (negative energy) and we assume that the field depends on boths tensor
fields, through the following formalism :
(115)
S = c ( T - T* )
(116)
S* = c ( T* - T )
which corresponds
to conjugated geometries :
(117)
S* = - S
Notice that it definitively does not mean that g* = - g !
Tensors T ans T* can be figured with mass densities r and r* and pressures p and p*.
Here we consider that r, r*, p and p* are all positive, in order to show that "this is the same sort of matter". The minus sign indicates that the "twin matter" behaves like a negative mass (and negative energy and pressure) matter. This system of field equations has been presented and studied in previous papers (references [13] to [15]).
16) A project : the hyperspace transfer model.
In referenced papers, steady state coupled solutions [16] and non-steady uniform
solutions ([14], [15] and [17]) have been presented. We intend to build non-steady
and non-uniform solutions of the system (115) plus (116). For example, consider
initial conditions where matter is present in our space-time fold F, the second
one, F*, being empty. The corresponding system would be :
(118)
S = c T
(119)
S* = - c T
...A
steady state solution of such a system was presented in a previous paper [16].
In such conditions matter is only present in the fold F. It may describe the
conjugated geometries corresponding to the presence of a neutron star in this
fold, ours, the adjacent portion of the second (twin) one F* being empty. Initially,
the two folds are not connected. The solution, outside the neutron star obeys
:
(120)
S = 0
(121)
S* = 0
...Then matter is poured into the neutron star, up to criticity. Specialists know that the first symptom of criticity if the suddent raise of the pressure up to infinite at the center of the (supposes spherically symmetric) neutron star, according to the Tolmann-Oppenheimer-Volkov (TOV) model (ref.[1], equation 144.22). We think that this rise acts on the local values of the constants of physics (light velocity, gravitational constant, mass). Models with "variable constants" were initially introduced by the authors ([18], [19], [20], and [14]). Later, others authors developped this new concept, in a somewhat different way [17].
...We
think that this would cause the birth of an hypertoroidal bridge, linking the
two folds. Then matter would (rapidly, at relativistic velocity) flow from fold
F to fold F*, through this passage. As shown above, this phenomenon inverses
the mass, see section 14, equation (110), so that the non-steady solution depends
on the system :
(122)
S = c ( T - T* )
(123)
S* = c ( T* - T )
At "the
middle of the process" T = T* . Then the solution obeys :
(124)
S = 0
(125)
S* = 0
...We think it's the real meaning of the Schwarzschild's geometry. It would correspond to a frame which belongs to a non-steady process.
...This non-steady solution is only a project of solution. It is not built yet. We don't know what would come from, how the complete process would look like.