3) Geodesics in a [r,j] representation.
Introducing
(6) in (14), with dr = thr dr
we get :
(17)
![]()
which gives
the [r, j] representation
of geodesics. When r tends to zero dj/dr
tends to a finite value, so that the tangent of the pitch angle :
(18)
![]()
tends to zero at the origin. The image of the Schwarzschild throat circle, in such representation, is a conical point.
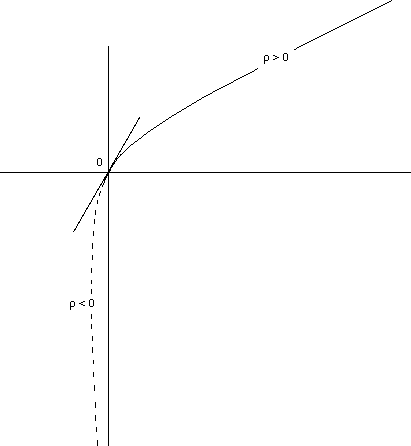
Fig.4
: The geodesic shown on figure 3, in a ( r , j
) coordinates system.
The crossing of the throat circle corresponds to point O
This an
isometric representation of the geodesics.
Notice we can also figure the surface in a [z, r ,j]
representation, but this is no longer an isometric one. We get the associated
meridian :
(19)
![]()
When r tends to zero z(r) is linear. When it tends to infinite, the function tends to a parabola.
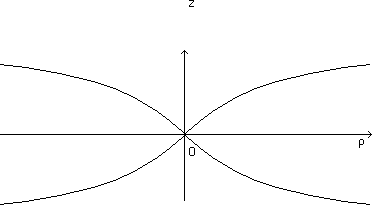
Fig.
5 : Meridian of the surface, in a [ r, j ]
non-isometric representation
of the surface.
The image of the Schwarzschild throat circle, in such representation, is a conical point.
4) Extension to a spherically symmetric 3d hypersurface.
This can
be extended to a 3d hypersurface, as described by the line element :
(20)
![]()
This metric refers to a 3d hypersurface, here expressed in a [ r , q , j ]. coordinates system. The variable r is not a "radial distance", corresponding to "spherical coordinates". We refind similar pathologies in this new line element, which can be eliminated, introducing the same coordinate change (6).
[ r , q , j ] ® [ r , q , j ]
Then this
line element becomes :
(21)
![]()
Its signature
becomes ( + , + , + ) and its determinant :
(22)
![]()
no longer vanishes.
The geodesics
of this hypersurface are located in planes. q = p/2
is one of them. In their [ r , j ] representation
they identify to those of figure 2. The isometry group is O3 and the corresponding
orbits are spheres. Among those, one owns a minimum area (the throat sphere
of such 3d toroidal bridge ). The great circles of the spheres-orbits
are not geodesic curves, except the peculiar ones located on the throat sphere
whose perimeter is 2 p Rs. The geodesics of this
peculiar sphere are the only closed ones. We can call this peculiar geometric
an hypertoroidal geometry . This 3d-surface is not simply connected.
It owns a single 3d fold, which can be considered a set of two bounded half
3d folds, glued together along their spherical border (the throat sphere). At
large distance from this "hypertoroidal bridge" the metric tends to
the euclidean one, hereafeter written in spherical coordinates :
(23)
ds2 = dr2 + r2 ( dq2 + sin2q dj2 )
5) Schwarzschild geometry.
Classically one considers that its isometry group is SO3 X R where R refers to one-dimensional translations. Then one uses to say that this metric in time-independent ands spherically symmetry, considering that R corresponds to time-translations.
Expressed in a [ x° ,
r , q , j ] coordinates system, where x° is the time-marker,
the line element is
(24)
![]()
Classically, one writes x° = ct , which is supposed to define the cosmic time t of "an external observer". When r >> Rs (21) tends to the Minkowski metric. Classically r is assimilated to a radial coordinate. (21) shows an irregularity of the term grr and a change of the signature when r = Rs .
Once again we can regularize this metric, using the (6) coordinate change, shifting
to a [t, r , q , j ] system.
Then the line element becomes :
(25)
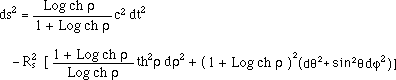
The orbits of the O3 isometry group are spheres. Among this set, one, the throat sphere (Schwarzschild sphere) owns a minimum area. The hypersurface is not simply connected. It forms a single space-time fold, which can be considered as a set of two half 4d space-time folds (twin folds), the first corresponding to r > 0 and the second to r < 0 , whence the throat sphere corresponds to r = 0. We may compute the geodesics, located in q = p/2 plane. Following : "spherical coordinates" :
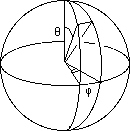
Fig.6 : Spherical coordinates.
the element is dr2 = r2 ( dq2 + sin2q dj2 )
The circles j = constant are geodesics of the sphere but, obviously, they do not represent all the geodesics of the surface. Only the ones passing by two antipodal points (poles).
The circles q = constant are not geodesics, except the one which corresponds to q = p/2 (equator).
In a [
r ³ Rs , j ] coordinates
system these (non zero length) geodesics correspond to :
(26)
![]()
The choice of the set of constants [ l , h ] determines the geodesic. Among them we find hyperbola-like geodesics, which do not intersect the throat sphere r = Rs. See figure 7.

Figure
7 : Schwarzschild geometry.
[ r ,
j ] representation
of hyperbola-like plane geodesic
which does not cut the throat
sphere r = Rs
We also find quasi-elliptic geodesics. See figure 8
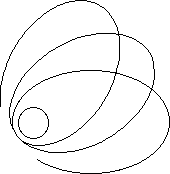
Fig.
8 : Schwarzschild geometry.
[
r , j ]
representation
of quasi-elliptic geodesics.
Now let
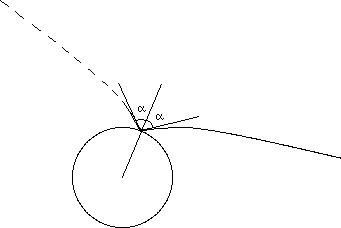
us focuss on geodesics which intersect the r = Rs throat sphere. In a [ r ,
j ] representation, call a the angle between
the tangent to the geodesic and the radial vector.
(27)
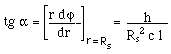
The first
Lagrange equation gives :
(28)
![]()
For r
³ Rs values the parameter l is strictly positive.
Another Lagrange equation is :
(29)
![]()
and gives a monotonic evolution of the angle j with respect to the proper time s. In this (q = p/2 ) plane the wirling depends on the sign of h .
According to this new interpretation of the Schwarzschild geometry (considered as a non simply connected hypersurface) we may figure the geodesic in a [ r , j ] representation as shown on figure 9.
Figure
9a : [ r , j ] representation of a geodesic
which intersects the throat sphere
(Schwarzschild sphere) corresponding to h ³ Rs
One portion of the geodesic has been figured as a dotted line, for it is supposed to belong to the second half-3d fold, linked to the first along the throat sphere, the Schwarzschild one. It suggests a break. But this last is due to this peculiar [ r , j ] system of representation, which is more familiar to our (poor) human geometric intuition. In a 3d representation space we get figure 9b. Particles are like "bouncing" on the Schwarzschild sphere.
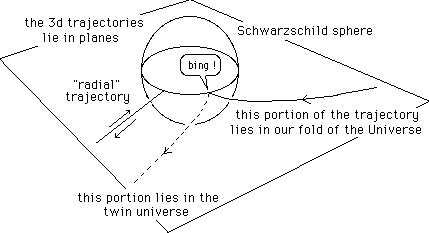
Fig.9b :
In the 3d euclidean representation space particles
are like bouncing
on the Schwarzschild sphere.
From this point of view, "there is nothing inside the Schwarzschild sphere", for, in this "inside" we are simply "out of the hypersurface". Recall that the throat sphere, the Schwarzschild sphere corresponds to the r = 0 value. The first half fold corresponds to ( r > 0 ) and the second one to ( r < 0 ) .
In a [ r , j ] representation, the aspect of the
geodesic becomes fairly different. Let us compute the tangent of the angle b
, between the geodesic and the radius vector (see figure 6).
(30)
![]()
When r
tends to ± 0 thr » r ,
whence :
(31)
![]()
In the [ r , j ] representation the geodesics which
go from one half fold to the other one are tangent to the radial vector. There
is no longer angular discontinuity at the origin, this last being the image
of the throat circle ( r = 0 ). To get a complete
description of these geodesics we must return back to the line element, as expressed
in the [ t = x°/c, r , q , j ] coordinates system
(24), using the Lagrange equations system, with :
(32)
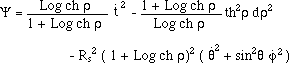
Among these
equations, we find :
(33)
![]()
For a given h value the evolution of j is monotonic, with respect to the proper time s.
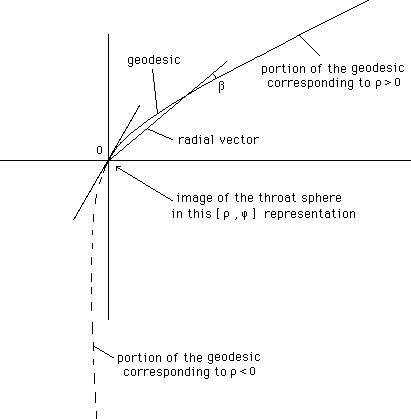
Fig.
10 : [ r , j ] representation of a geodesic
which passes
from a half-fold
( r > 0 ) to the other one (
r < 0 ).
As before, the portion of the geodesic which belongs to the second 3d half-fold has been figured as a dotted line.
We cannot give an imbedding of the 4d hypersurface, as we did at the begining of the paper for a 2d surface. By the way, we deal with 4d geodesics, not 3d ones. [ r , q , j ] and [ r , q , j ] spaces are nothing but representation spaces, which are supposed to make the things a little bit clearer. The real geodesics are inscribed in a 4d space. Anyway, the [ r , q , j ] representation suggests some 3d "hypertoroidal bridge", whence the [ r , q , j ] representation suggests some 3d "hypercone". In this second (3d) representation of such 2d surface they are geodesics which go from one half-fold to the other one, passing through the ( r = 0 ) point. This is similar to a 2d-cone. See figure 11
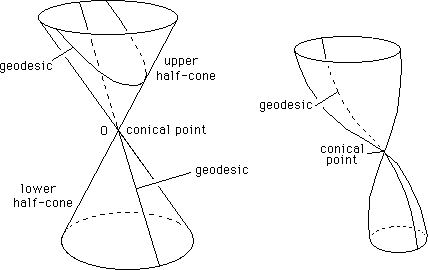
Fig. 11
: Geodesic of a cone. Right :
a
surface owing a conical point.