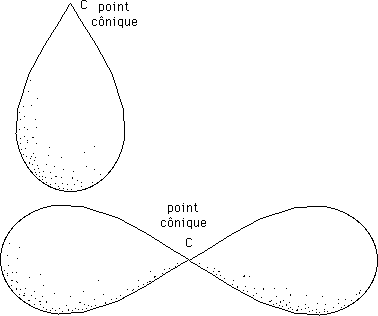
Mais il existe de surfaces qui sont intrinsèquement singulières, possédant des singularités qui ne sont pas dues à un choix de coordonnées. Exemple ci-après : la singularité conique.

Brute de fonderie, telle que formulée en 1917 par Schwarzschild dans des coordonnées t , r , q , j (le temps, une distance radiale et deux angles, équivalant à azimut et site : des coordonnées "sphériques") la sphère de Schwarzschild est singulière. Pour une certaine valeur Rs de la "coordonnée radiale" r (censée être mesurée depuis un "centre géométrique") cette métrique nous joue les pires tours. Sur cette sphère un des terme a un dénominateur nul. Bref, elle est singulière sur cette sphère. S'agissait-il d'une singularité intrinsèque ou d'un artefact induit par un mauvais choix de coordonnées ? C'est la question que nous nous sommes posée.
Notons au passage que la "géométrie de Schwarzschild" est une hypersurface à quatre dimensions, ce qui rend la chose encore plus malaisée.
Kruskal s'est focalisé sur ce point. Il a construit un changement de coordonnées qui, entre autre, fournit une valeur constante de la vitesse de la lumière le long d'une trajectoire radiale. Ce faisant il concentre l'aspect singulier "au centre de l'objet", dans une "singularité centrale". Psychologiquement, on a l'impression d'y gagner. La solution devient "régulière presque partout", expression que les mathématiciens utilisent pour dire que la solution est régulière, exempte de pathologie, sauf en un unique point.
- Vous n'allez pas chipoter, me chercher querelle, pour un simple point.....
Hélas cette formulation de Kruskal a un grave défaut : elle ne redonne pas l'espace de la relativité restreinte à l'infini. Techniquement, elle n'est pas lorentizenne à l'infini, "asymptotiquement lorentzienne".
C'est une question essentielle en physique : les singularités existent-elles ? La Nature tolère-t-elle des singularité ? La réponse se formule en termes de croyance (comme pour l'existence ou l'inexistence de l'infini d'ailleurs).
Nous avons cherché une nouvelle interprétation de cette même géométrie de Schwarzschild en essayant d'éliminer toute singularité et nous y sommes parvenus. Notre réponse est donc :
- Le caractère singulier de la solution de Schwarzschild est simplement induit par un mauvais choix de coordonnées.
Techniquement, tout repose dans le changement de variable :
r = Rs + Log ch r
qui se lit " r égale Rs plus logarithme du cosinus hyperbolique de la variable r ". Simple a parte pour scientifique, spécialiste ou simple taupin. Pour qui sait manier cette formule, la grandeur r ne peut alors plus devenir inférieure à Rs, même quand r prend toutes les valeurs possibles en moins l'infini et plus l'infini.
Considérez une surface qui soit obtenue en faisant tourner une parabole autour d'une droite, comme ceci :
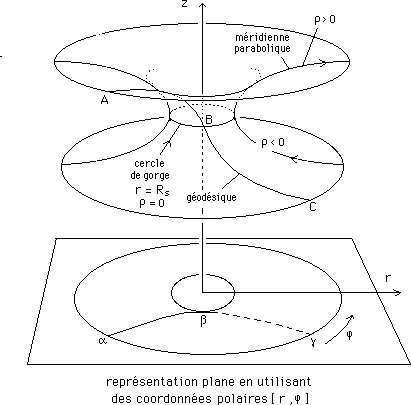
Cette figure est extraite de l'article. La surface est infinie, en fait, comme la parabole-méridienne qui l'engendre en tourant autour de l'axe z, figuré.. Si on tient absolument à se la représenter avec des coordonnées (r,z,j) on peut s'attendre à de ennuis quand on se demandera "comment est cette surface pour r < Rs ?"
On trouvera une réponse .. imaginaire, avec des racines de quantités négatives. Tout simplement parce qu'on est alors "hors surface".
Cette surface, en mathématiques, est dite "non simplement connexe", terme barbare qui désigne simplement les surfaces où toute courbe fermée ne peut voir son périmètre décroître, en faisant glisser celle-ci dans la surface, jusqu'à prendre la valeur zéro.
C'est possible sur une sphère, qui est "simplement connexe". Mais sur cette surface-là on voit bien que toute courbe fermée qui "fait un tour autour de cette espèce de puits central" ne pourra voir son périmètre tendre vers zéro, la limite étant le périmètre du "cercle de gorge". Même chose pour un tore, qui est aussi "non simplement connexe".
Nous avons défini une telle surface en partant de sa métrique, ce qui illustre très bien le propos. En gardant la coordonnée r, cette surface semble singulière. En utilisant le changement de variable donné ci-dessus, elle ne l'est plus. A quoi correspond cette coordonnée r ? Elle "court" simplement le long de la parabole méridienne comme indiqué sur la figure, prend la valeur zéro sur le cercle de gorge. La moitié de la surface correspond à r positif, l'autre à r négatif. Dans le système de repérage des points [r , j ] il n'y a plus de singularité.
Nous avons décidé d'appeler ce type d'objet un "pont torique", par analogie avec le tore.
Mais on montre aisément, toujours en partant de métriques, qu'on peut passer à un objet, une hypersurface 3d, qui comporte un "pont hypertorique". Il n'y a alors plus un cercle de gorge, mais une sphère de gorge. De même que pour la surface ci-dessus, un cercle de gorge semblait mettre en communication deux nappes 2d, la sphère de gorge met alors en communication deux "demi-espaces 3d". Quand on est dans un de ces demi- espaces 3d et qu'on plonge dans la sphère de gorge, on émerge dans l'autre demi-espace.
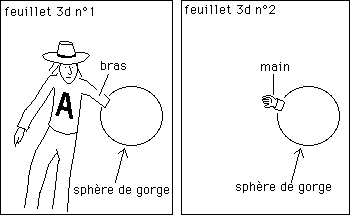
Revenons à la surface 2d montrée plus haut. Le dessin ci-après montre qu'en traçant "des cercles que l'on croît être concentriques" on voit leur périmètre diminuer, passer par un minimum, puis croître de nouveau.
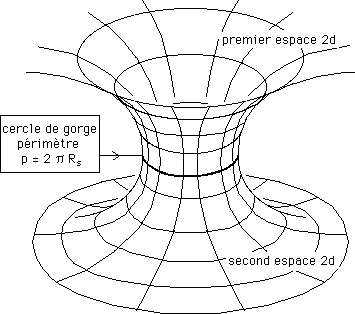
En 3d il faut imaginer une sphère entourant complètement la sphère de gorge. Puis une autre, à l'intérieur de celle-ci (on devrait dire "au-delà" en suivant une direction donnée, vers cette sphère de gorge). On imagine que la surface de cette sphère puisse être plus petite. Mais, quand on atteint la sphère de gorge, l'aire passe par un minimum, puis se remet à croître... jusqu'à l'infini, lorsqu'on prolonge l'opération.
Nous avons construit les "métriques" de ces surface 2d et 3d comportant un "passage torique" et un "passage hypertorique" et, dans le second cas, nous avons été frappés par la ressemblance avec la métrique de Schwarzchild, où nous avons donc opéré ce changement de coordonnées, faisant apparaître son caractère "non-simplement connexe", "l'intérieur" de l'objet devenant simplement "l'au-delà de sa sphère de gorge".
Il a ainsi été possible d'éliminer toute singularité.
A ce stade nous avons simplement étendu le modèle du trou noir à un tandem "trou noir-fontaine blanche". Mais, toujours pour cet "observateur extérieur", le temps de traversée de ce pont hypertorique était toujours infini. Nous semblions avoir simplement amélioré le modèle du trou noir en expliquant sur quoi il débouchait.
Nous avons dit que le choix des variables était, dans une solution géométrique, totalement arbitraire. Mais ce qui vaut pour l'espace est aussi valable pour le temps. Nous sommes donc allés chercher un changement de variable temporelle inventé par Eddington en 1924 :
![]()
Là encore, nous le mentionnons pour le scientifique ou simple taupin.
t est l'ancien "temps cosmique", l'ancienne "variable chronologique" présente dans la solution initiale de Schwarzschild, de 1917.
t' est ce nouveau "temps d'Eddington". Rs est le "rayon de Schwarzschild (on devrait alors parler de périmètre de Schwarzschild, divisé par 2p ).
c est la vitesse de la lumière (ici, constante).
Chose qui peut sembler bizarre : on mélange le temps et l'espace mais, en la matière, on a tous les droits. Le choix de la coordonnée temps, de la coordonnée de repérage chronologique (time-marker) est totalement arbitraire. On demande simplement :
- à la métrique d'être asymptotiquement Lorentzienne, c'est à dire qu'à l'infini, l'espace temps devienne l'espace temps de Minkowski, celui de la relativité restreinte. Dans notre cas, ça marche (pas chez Kruskal).
- à ce nouveau temps t' de s'identifier, toujours à l'infini, au "temps propre d'un observateur supposé immobile". C'est aussi le cas (pas chez Kruskal)
Ce faisant le temps de chute libre d'une particule-témoin, immobile à l'infini et tombant vers la sphère de Schwarzschild, devient infini, vis à vis du temps vécu par "l'observateur extérieur", qui est loin et immobile.
La particule, par contre, émergerait de cet "aven" en un temps infini. Comme dans le trou noir on peut donc entrer dans cette sorte d'aven 3d, mais non en sortir, sinon en un temps infini.
L'autre côté est une "résurgence". Mais, avec un tel choix du temps (t') la particule émerge de cette résurgence en un temps infini, alors qu'elle peut y pénétrer en un temps fini. Ca coinçait quelque part. La solution a consisté à effectuer, ce qu'on a parfaitement le droit de faire, une sorte de double changement de variable. Pour le bout d'espace temps qui est supposé être le nôtre :
![]()
Dans "l'univers jumeau" :
![]()
Le mécanisme cosmique fonctionne alors parfaitement.
- Pas de singularité.
- On peut entrer dans "l'aven" mais non en sortir (trou noir)
- On peut sortir de la résurgence, mais non y pénétrer (fontaine blanche).
Bien, me direz-vous, on progresse....
Oui et non. Le temps de transit de la matière dans ce passage hypertorique est de quelque dizaines de millièmes de seconde, et ce Moloch est capable d'avaler n'importe quoi, dix masses solaires, par exemple, en moins de temps qu'il en faut à une balle pour traverser une carte à jouer.
La conclusion est qu'à travers cette réinterprétation plus rationnelle de la solution géométrique les trous noirs ne pourraient pas exister. Ce sont des ... fictions mathématiques. Ils ne pouvaient qu'exister qu'en vertu de ce "gel du temps". Or avec ce "temps d'Eddington" qui satisfait à toutes les exigences de la physique, le temps de transit devient fini.
Conclusion : cette géométrie de Schwarzschild ne serait, selon nous, qu'une image instantanée d'un processus instationnaire de transfert hyperspatial. C'est un peu comme si on vous montrait une photo d'une enclume que quelqu'un aurait lancée en l'air et que vous en concluiez que les enclumes peuvent flotter dans l'air.La solution de Schwarzschild est également solution d'une équation qui implique que l'univers soit parfaitement vide, que la densité d'énergie matière soit nulle en tout point. C'est alors un peu comme si on vous montrait une photo d'un terrain de foot, prise quand les joueurs sont partis se reposer pendant la brève mi-temps et que vous en concluriez que le football se joue sur un terrain.. vide.
Mais alors, que se passerait-il ?
Nous avons montré que lors du passage de la sphère de gorge la coordonnée temps s'inversait. Si on appelle t' le temps (d'Eddington) correspondant à notre "versant d'espace-temps" et t'* le "marqueur de temps" de l'univers jumeau, on a :
t'* = - t'
Remarquons qu'Andrei Sakharov a été le premier à suggérer en 1967 que se soient créés au moment du "Big Bang" deux univers jumeaux ayant des temps opposés.
Restait à savoir ce que signifiait le sens de cette "inversion du temps". Etait-ce à dire que lorsqu'on plongeait dans l'univers jumeau on rajeunissait ? Nous avons montré que non. On "emmène son temps propre" et si on ressortait un peu plus loin par une structure symétrique, on n'émergerait pas plus jeune que quand on est entré dans cet univers jumeau. Impossible de "tuer son propre père" comme dans le thème du "Voyageur imprudent", de Barjavel.
Les groupes, encore, nous ont permis d'élucider le sens "ontologique" de cette inversion de la coordonnée temps. Quand une particule plonge dans l'univers jumeau, son action gravitationnelle se fait toujours sentir, mais sa contribution au champ gravitationnel devient alors négative. Sa "masse gravifique" s'inverse.
Au passage, ceci justifie totalement le modèle développé dans le site et dans l'ouvrage "On a perdu la moitié de l'univers" (Albin Michel). Les masses qui se baladent dans l'univers jumeaux se comportent vis à vis des masses présentes dans le nôtre comme des masses répulsives. La dynamique complète est :
- Dans notre univers les masses s'attirent selon Newton
- Dans le jumeau les masses s'attirent selon Newton
- Quand des masses situées dans deux portions "adjacentes" de l'espace temps interagissent, elles se repoussent.
C'est une simple conséquence de cette inversion de la variable temporelle (mais non du temps propre).
Les groupes montrent aussi que la dualité matière antimatière existe dans les deux univers, comme conjecturé par Andrei Sakharov.
Quand une particule de matière réussit à passer dans l'univers jumeau (on verra plus loin comment) elle reste de la matière, mais "CPT symétrique". C'est le sens du fameux "théorème CPT" de la physique (jamais démontré. Ce que Souriau appelle un "théorème de physicien"). Classiquement les physiciens disent "la CPT symétrique de la matière est identique à la matière". Par CPT symétrie, entendre :
- La particule, dans ce nouveau repère, chemine à "rebrousse temps" : T-symétrie.
- Elle est énantiomorphe, inversée droite-gauche, "en miroir" : P-symétrie.
- Toutes ses "charges" sont inversées, y compris sa charge électrique, si elle en possède une. C'est la C-symétrie.
Pour nous, la CPT symétrique d'une particule est une particule du jumeau (ou passée dans le jumeau). C'est une particule gémellaire. Comme il y a T-symétrie, sa masse est automatiquement inversée (résultat initialement obtenu par J.M.Souriau en 1974).
La C-symétrique d'une particule est son antiparticule.
Feynman avait trouvé que la PT-symétrique d'une particule se comportait comme une antiparticule. Exact, mais il s'agit de .. l'antimatière du jumeau, à masse négative (puisqu'il y a aussi T-symétrie). Tout cela émerge d'histoires de groupes Ce travail fait le lien avec tout ce qui avait été publié jusqu'ici (dans le site, voir Geometrical Physics B au rayon "géométrisation de l'antimatière"). On peut illustrer de façon parlante cette affaire d'inversion de l'espace. Dans le papier, on insiste pas mal sur la notion d'espace de représentation. C'est l'espace dans lequel nous nous représentons mentalement le objets géométriques. Nous avons utilisé plus haut une image où on voyait Lanturlu enfiler sa main dans cette sphère de gorge, laquelle semblait émerger dans un autre univers 3d. Pour des commodités de dessin on a séparé les deux figures. Mais il y a une chose vous n'aurez sans doute pas remarqué de prime abord : Lanturlu enfile dans cette sphère une main gauche et c'est une main droite qui en émerge. Cela n'avait pas été fait par hasard.
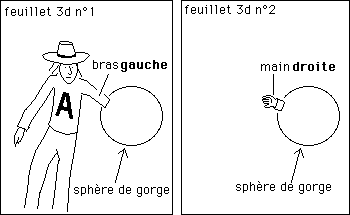
Où est ce second univers ?
Il est imbriqué dans le nôtre, ce qui et difficile à comprendre. Mais ceci sera plus simple en revenant à la surface 2d, au "flatland".