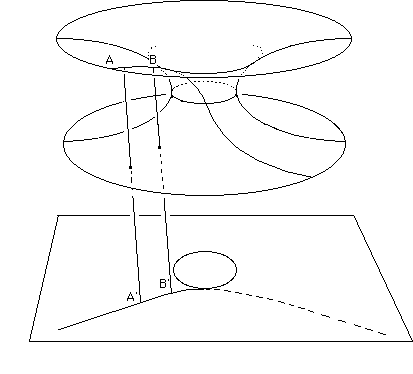
We have "cleaned up" the figure here to make it a little more legible. A surface is a 2d object, here "plunged" into an otherwise Euclidean 3d space in R3. We can "see" it from above. It so happens that this surface is plungeable in the space R3 "in an isometric manner". That is to say that if we stick some tape on it, this will effectively inscribe itself on a geodesic joining two points of the surface A and B. The length measured along the geodesic arc is also correct. It is iso-metric, etymologically "the same length". Below there is a 2d representation that is not isometric ... the length of the arc A'B' is not equal to that of arc AB. Construct the following object with the aid of a sheet of paper, a pencil and a pair of scissors :

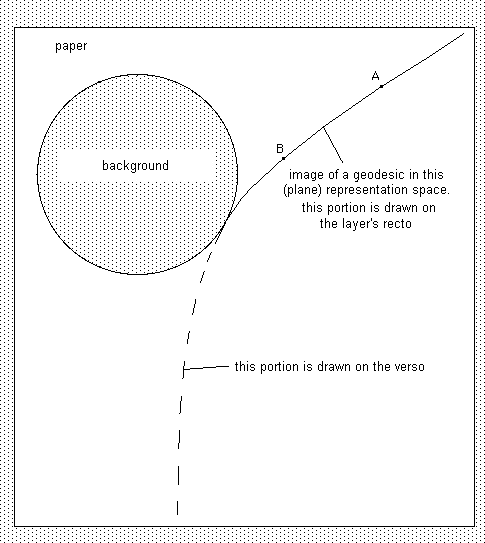
    This drawing is not isometric. First of all the curve shown is not a geodesic of the plane. Secondly the width of the arc AB is not the "real length" that could be measured on the "real surface", which "has no hole". The sheet of paper with a hole is just a useful representation, nothing more. The same goes for the technique of drawing on one side of the sheet then the other, the whole curve only appearing in transparency.

    In the following figure we have shown the geodesics of the surface, calculated by computer (which features in the article).

    The dotted lines of the curves correspond to the branches on "the other side" (as if we were looking at the surface "from above").

The arc BC crosses the sphere of the gorge. Same thing.

    But this isometry does not apply to all the geodesics of the surface. One exists, unique in its way : the gorge circle, reduced here to a point. It is the only surface that closes on itself.

   Geodesics are the only things we have to understand a surface or, more generally, a non-planar, non-Euclidean space. They are useful markers (even if we have a distorted view in our 2d and 3d representation systems (in perspective)). We know that these geodesics exist, that they are intrinsic. Those of a sphere, for example, are large circles. In the case of space-time, they are filled with an infinity of spatio-temporal geodesics. The geodesics exist intrinsically and to understand them (etymologically : hold, take in one's arms) we try to "feel" them like blind men. However space and time coordinate lines have no intrinsic reality, nor are the two meridian and parallel ensembles an integral part of a sphere. They are not "supplied within". Schwarzschild's geometry, a solution to Einstein's field equation, is a 4d hypersurface. Theoreticians have stuck whole families of curves on it, "constant t", "constant r" etc.
  Never forget that these gestures are totally arbitrary, though even specialists in theoretical cosmology often lose sight of this point and, from time to time, have to be called to order by geometry-mathematicians. It was therefore perfectly licit to change space-time coordinates.

    At this point you'll be saying : so what tells us that one choice of coordinates is better than another ? What is reasonable and unreasonable ? It is a question of taste. Choosing space-time coordinates means placing a physical vision on a mathematical object. In the case of the Earth, we have given it poles when it rotates. The North Pole is simply the normal of the surface "Earth" that points towards the Pole Star, a star that remains fixed in the heavens.

    In the matter of isometry and non-isometry, cartography illustrates the difficulties in trying to represent a sphere on a plane. Mercator's projection (projection of the Earth's sphere onto a cylinder tangent to the Equator) is very nice for those who live near the Equator. However someone who lives at one of the poles is in for a nasty surprise : his punctual domain turns into a straight line...

    There are hundreds of ways of projecting a sphere onto a plane. Let us imagine this :

    Imagine that we make maps from this model and we sell them. An instant success among those who live at the two poles : the projections are quasi-isometric in these regions. Useful for getting an idea of distances in those areas. If Earth had been habitable at the poles and relatively inhospitable elsewhere, maps would no doubt have been made like this. However we would see that the border circle of the projection on a plane no longer corresponds to the Equator but to a parallel (in the northern hemisphere here). Near this region the map will be way off isometry. As well as that, on this strange map, a part of the landmass should be shown with a normal, full line and part with a broken, dotted line because it is situated beyond the parallel where the object, oddly, seems to "fold back on itself". Perhaps we could supply maps on a paper disc with the rest of the landmass appearing on the other side of the sheet.

    Let us try to "imagine all that in 3D". We showed Lanturlu plunging his left arm into the gorge sphere via two separate drawings, which could seem to imply that the second 3D space is "elsewhere". To be correct the two perspective drawings should be superposed with the emerging (right) hand represented by a dotted line.

    Obviously "inside" the gorge sphere there is nothing. The appearance of an interior, a volumetric content, is just due to our choice of this 3D representation space. Just as in the hole cut in the sheet of paper there is no paper either. It was just an accident linked to the choice of this planar representation space. If someone insisted on using a planar representation without removing the disc cut in the paper and who repeatedly asked "what's inside" they would be completely "off the field" (or rather ... in it). The field doesn't exist.

    Let us return to 3D. When Lanturlu plunges his arm in the gorge sphere this doesn't have an interior either. The appearance of an interior is simply due to our choice of representation space. We could consider that Lanturlu and his emerging hand have been drawn on a sheet of paper having three dimensions and from which we had removed ... a sphere (the 3D equivalent of the disc of the sheet of paper). Mathematically, a disc is a "b2 ball" and a "sphere volume" is a "b3 ball. By "ball" we mean a contractile cell (see the Topologicon on the "CD-Lanturlu") that is to say an object which can contract in relation to a point by going over itself. The 2d and 3D examples are there to illustrate the article's battle plan : the Schwarzschild sphere has no "interior", no "centre" When we cross it (hypertoric passage) we find ourselves on the "other side of space-time".

    What is the justification for this new interpretation of "Schwarzschild geometry" ?

    Answer : the elimination of singularities. Kruskal, with his "analytic prolongation", did everything possible to penetrate this "blasted sphere". He only managed to pack the singularity (a role initially held by the Schwarzschild sphere) in a point situated "at the centre of this object". People satisfied themselves with this conjuring trick. However we think that it's better without singularity.

    Nature protests, when we look at it from the wrong side, by secreting singularities. That is how we see things. It is a preconceived view of what is "real". We believe that these singularities do not exist in nature. We also think that infinity doesn't exist either. But as Kipling said, that's another story. I had animated discussions with Souriau on the question a year ago.

    - What proves that infinity exists ? ....

    - But, without infinity there is no mathematics ! ....

    - Have you ever met infinity ? Seen it, held it in your hand ?

    - It's a .... convenience.

    - We generate infinitely large numbers by supposing that we can add 1 to a number indefinitely. We are using a sequential infinity to generate a numeric infinity. It eats its own tail, your thing.

    - OK, let us say that it's a convenience. Man has invented two things of importance during his history : infinity and toilets ...

    Nor do I believe that the infinitely small exists, either physically or mathematically. But that will be the subject of other papers. Let us leave these questions aside for the moment. A simple digression.

    In passing, see "Scale Invariant Cosmology" by P. Midy and J.P. Petit, International Journal of Modern Physics D, June 1999, pages 271-280 where we made "the initial singularity of the universe" disappear. It is a more mathematically constructed reformulation of an idea I published in 88-89 in Modern Physics Letters A (papers on the site).

    As Archimedes said, I believe, at the entry to a sanctuary of science, " no one enters here who is not a geometrician". These tensors and stuff, a field that Midy loves, are as indigestible as English pudding.

    We can see therefore, through this discussion, that our physical vision of these phenomena comes from the way we decide to represent them. In modifying spatial coordinates we have changed "local topology", a term which requires a mathematical clarification according to Souriau. In fact the phrase is a gentle euphemism : he simply began to rave when I said it and his cat Pioum and I had the greatest difficulty calming him down. Souriau is the Professor Tournesol of mathematics. He is a willing practitioner of high mathematical indignation. However this indignation should not be confused with anger in the trivial sense of the word. Rather, that I play Molière's "Monsieur Jourdain" is this area. Physicists often use mathematics without knowing it (and vice-versa in fact).

    In admitting, provisionally, the use of "non specified" words, everything happens as if we had considered only that "local topology" of Schwarzschild geometry was "hyperspheric" (that the Schwarzschild sphere "contains" a "B3 ball"). We have made it "hypertoric". That's why I proposed the term "hypertoric geometries".

    We mentioned earlier the inversion of space. It is negotiated with the groups. Can we understand that differently ? We saw that Lanturlu plunged his left hand into the gorge sphere and saw a right hand come out. In fact each atom of his hand followed a "radial" geodesic, perpendicular to the surface.

    Let us not forget to mention in passing that this system of representation is not isometric. As with the paper with a hole. If we measure the distance covered in the two half spaces by a test atom belonging to Lanturlu's hand (Archibald Higgin's in English issues) it would not coincide with the real distance measured with a piece of string.

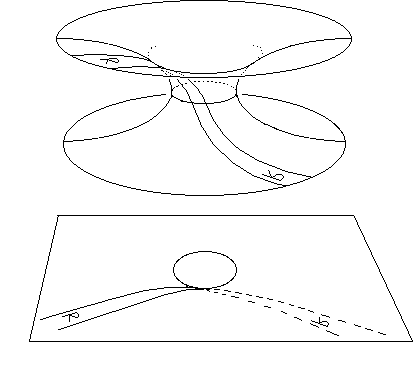
    Let us return to the figure shown previously.

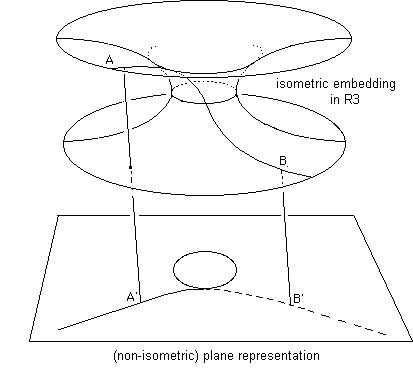
    Here we have shown a geodesic arc AB that crosses the gorge circle and its image in the planar representation space below. The non-isometric character of the representation becomes even more apparent. The lengths of the arcs AB and A'B' are very different.

    Obviously it is fairly difficult to imagine that we can thread a string into the gorge sphere of a hypertoric passage. In tightening the string we would obtain a geodesic (line of the shortest path). After all, if we measured the length of the string in the 3d representation space (Lanturlu pushing in his arm) and we decided to measure the length of the string in this space, we would find a shorter length A'B'. The real length, measured in the 3d hypersurface, would be longer, as shown in the 2d drawing. The 3d representation with Lanturlu is therefore non-isometric, as is the planar representation above.

    With the help of a few drawings these subtle concepts, developed from group theory, become less hermetic providing one "sees into space". That's what I'm trying to teach you how to do, see into a 3d curved space.

    We have shown a sort of ribbon whose edges are made of two geodesics. What do we notice ? In the representation space the letter R is inverted to become a Russian "ia", a reversed R, enantiomorphic. We are starting to understand why Lanturlu's hand seems to be inverted when it emerges in the "3d representation space", it becomes enantiomorphic.