Représentations polyèdriques de différentes surfaces.
Permutation des points cuspidaux d'une Cross cap.
Transformation d'une surface de Boy "droite" en surface de Boy "gauche", via la surface Romaine de Steiner.
Inversion "droite"-"gauche" d'une surface de Boy.
Résumé :
On présente quelques éléments permettant de représenter des points de courbure concentrée : "posicônes", "négacônes" et leurs équivalents polyèdriques : "posicoins" et "négacoins", qui permettent de construire des représentation polyèdriques de différentes surfaces, et de retrouver leur courbure totale. Ainsi la représentation polyédrique de la surface Romaine de Steiner est constituée par quatre cube accolés selon leurs arêtes, ce qui la rend plus intelligible. Une représentation polydérique de la surface de Boy avait déjà été donnée dans le Topologicon, 1985, Editions Belin, pages 48 et 49, sous forme d'un découpage, à construire. Page 46 figuraient également des représentations polyédriques du tore et de la bouteille de Klein. Des représentations polyédriques de la Cross-Cap sont données. La courbure totale des différentes immersions du plan projectif dans R3 : surface de Boy, Cross-Cap, surface Romaine de Steiner vaut 2p. La représentation polyèdrique des points cuspidaux, considérés comme des points de courbure concentrée permet calculer celle-ci, très simplement. Cross-cap, surface Romaine de Steiner, surface de Boy se présentent comme "les multiples visages" d'un objet unique : le plan projectif. Comme ceci n'a rien d'évident au premier coup d'oeil, on construit des transformations géométriques qui permettent de passer de l'une à l'autre. On part de la Cross-Cap qu'on transforme en surface Romaine de Steiner en y créant deux points cuspidaux supplémentaires (c'est à dire qu'on met en oeuvre, dans ce sens, la modification générique "création-décréation de points cuspidaux"), puis on transforme la surface de Steiner en surface de Boy par confluence de paires de points cuspidaux. Accessoirement, en utilisant le fait que le plongement standard de la sphère puisse être transformée en son plongement antipodal (retournement de la sphère) on montre que les deux points cuspidaux d'une Cross-Cap peuvent être échangés par une succession d'immersions, la transformation illustrant le fait que ces deux points sont équivalents.
PREAMBULE :
Le lecteur retrouvera ici des éléments généraux qui se trouvent également dans l'introduction de GEOMETRICAL PHYSICS A (définition des posicones, négacones, etc). S'il veut sauter ce passage il n'a qu'à cliquer ici.
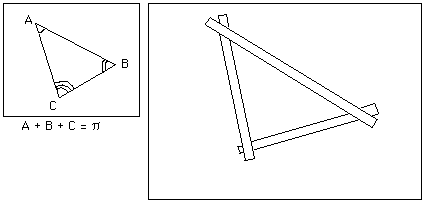
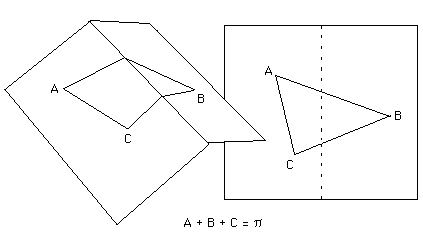
Si on trace sur un plan un triangle composé de droits segments de droites, la somme des angles aux sommets vaut p . Ces droites du plan peuvent être obtenue différemment : en collant sur la surface des bandes d'un ruban adhésif quelconque, sans faire de plis. On appelle alors ces trajets du plan des géodésiques. On peut tracer des courbes géodésiques sur n'importe quelle surface par ce procédé, par exemple sur l'aile d'une automobiles, ou sur son capot.

POSICONES ET NEGACONES
Opérons une découpe dans un plan. et recollons les deux bords, puis traçons un triangle avec notre ruban de scotch, constitué de trois géodésiques de ce cône.
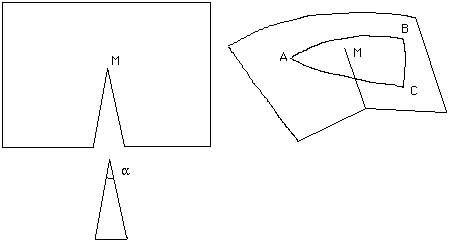
En séparant les deux lèvres de la surface, selon la découpe opérée précédemment ( figure 3 ) on s'apercevra aisément, en utilisant un rapporteur, que la sommes des angles A, B et C est égale à p plus l'angle de découpe a . Cet écart à la somme Euclidienne, nous l'appellerons courbure et nous dirons que le triangle "contient" une certaine quantité de courbure angulaire a. Cet écart sera le même quel que soit le triangle, si celui-ci contient le sommet du cône. S'il ne le contient pas la somme vaudra p . Nous dirons que la courbure est concentrée au sommet M du cône, qui est alors un "point de courbure concentrée". Comme la somme des angles est supérieure à la somme Euclidienne, nous dirons que cette courbure est positive. Ainsi un plan serait, dans cette optique, une surface à courbure nulle.
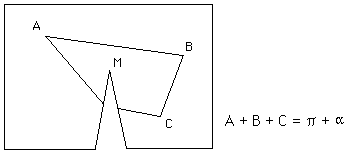
Cette courbure est additive. Si vous collez ensemble plusieurs de ces cônes vous, correspondant à des angles a , b , g , vous pourrez tracer toutes sortes de triangles constitués d'arcs géodésiques. Si le triangle entour trois points correspondant à des courbures contrées égales à a , b , g , alors la somme de ses angles au sommet vaudra : p + a + b + g .
On peut considérer une surface à courbure positive comme une sphère comme un assemblage d'une infinité de "posicônes". Au lieu d'avoir une courbure concentrée en différents points, on aura une courbure répartie uniformément sur toute la surface. On dira que la sphère est une surface "à courbure constante" (ou à "densité de courbure angulaire constante").
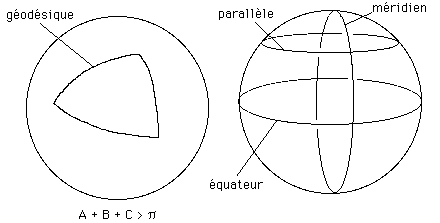
Sur la sphère, les géodésiques sont des "grands cercles". L'équateur et les méridiens sont des grands cercles, ce sont des arcs géodésiques de la sphère. Mais vous ne réussirez pas à créer un parallèle avec un ruban de scotch. Les parallèles ne sont pas des géodésiques de la sphère. La somme des angles au sommets d'un triangle tracé sur une sphère dépend du rapport entre la surface du triangle et celle de la sphère. La somme des angles d'un tout petit triangle sera très proche de p .
Un triangle dont la surface ferait un huitième de la surface de la sphère aurait une somme
Un grand cercle de la sphère peut être considéré comme une "triangle", à condition d'un placer les trois sommets... n'importe où sur ce cercle. La somme A + B + C vaudra 3 p. Il contient la moitié de la surface de la sphère.
Quel est l'écart maximal ? On ne peut pas dire "agrandissons" le triangle en allant au-delà de ce grand cercle, puisqu'au delà la longueur des arcs géodésiques constituant ses côtés vont diminuer et même tendre vers zéro.
Lorsqu'on a enserré toute la surface de la sphère on obtient
Nous dirons que la courbure totale de la sphère vaut 4 p.
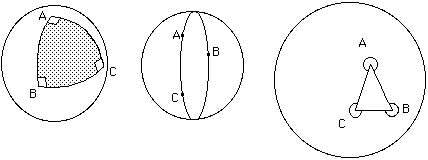
La quantité de courbure contenue par un triangle correspond à une simple règle de trois :
Nous allons maintenant créer un "négacône", en insérant cette fois un secteur angulaire a dans un plan, comme indiqué sur la figure 6
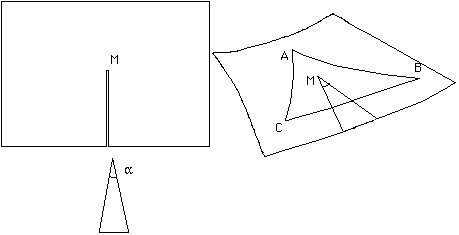
Quand on supprime le secteur angulaire on obtient ceci :
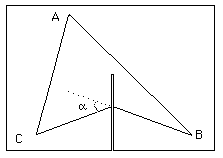
La somme des angles du triangle vaut A + B + C = p - a
Nous dirons que cette surface est un négacone possédant un point de courbure concentrée, négative. Cette courbure est aussi additive. En composant une surface avec une juxtaposition de mini posicone et de mini négacone on peut créer une surface où la valeur locale de la courbure soit quelconque.
La figure 7 est une surface à courbure négative distribuée. On dira aussi que cette surface possède, en tout point, une densité de courbure (angulaire). L'écart ( négatif ) vis à vis de la valeur Euclidienne de la somme des angles dépendra ici aussi de la surface du triangle. Plus celle-ci sera petite et plus cette somme sera proche de p.
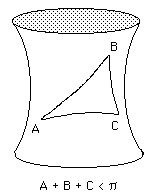
La figure 8 montre un exemple de juxtaposition de trois régions, à densité de courbure positive, négative et nulle.
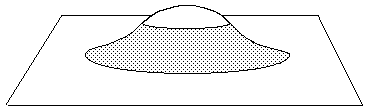
Si on trace des géodésiques on obtient ceci :
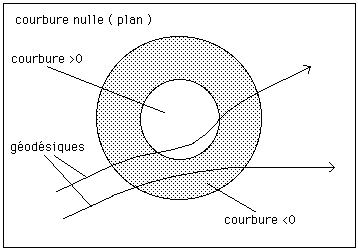
Dans l'exemple choisi la quantité de courbure contenue dans la calotte sphérique est égale et opposée à cette du congé de raccord ( on suppose que le plan tangent varie continûment ). Témoin la figure 10, ci-après :
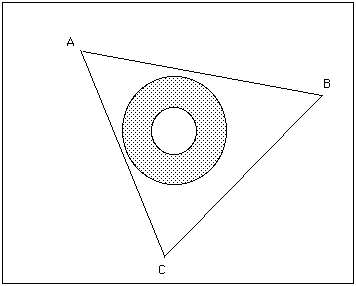
Certaines surfaces, comme le cylindre, nous semblent posséder une certaine courbure. Mais si vous tracez sur celui-ci un triangle à l'aide d'arcs géodésiques, et que vous mettiez ensuite le cylindre à plat (comme les posicônes et les négacônes, le cylindre est "développable " ) vous constaterez que la somme vaut 180°. Le cylindre, vis à vis de cette définition de la courbure, est "plat".
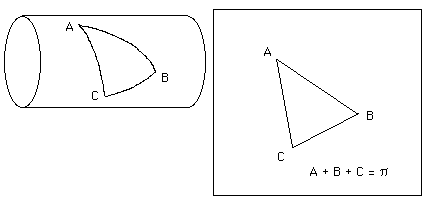
Un pli n'introduit aucun effet de courbure, et vous pourrez également le vérifier, avec votre ruban de scotch.
Les "coins" sont des points de concentration de courbure.Les arêtes ne contiennent aucune courbure. Les figures 6 et 7 montrent comment créer un posicoin correspondant à une courbure concentrée égale à + p / 2 et un négacoin à une courbure concentrée égale à - p/ 2 .
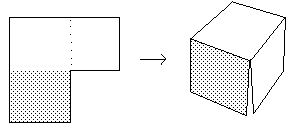
Fig. 13 : Création d'un posicoin de + p/2
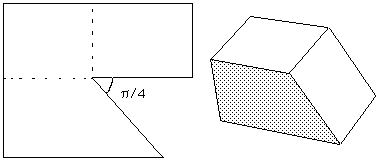
Fig.14 : Création d'un posicoin de + p/4
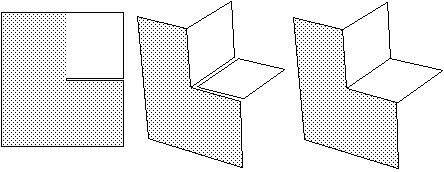
A l'aide de huit posicoins on peut créer un cube qui est une des représentation polyédriques de la sphère.
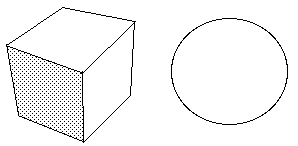
On retrouve la courbure totale de la sphère : 4 p
Avec huit posicoins et huit négacoins on peut créer une représentation polyédrique du tore et retrouve sa courbure totale : zéro.
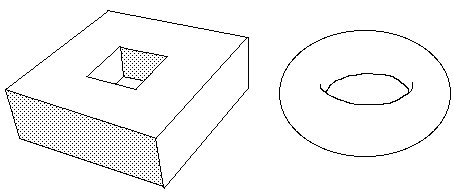
POINTS CUSPIDAUX
La Cross-Cap est un des multiples visages empreintés par le plan projectif dans R3. Il ne peut y être plongé. La Cross-Cap possède un ensemble d'auto-intersection qui se présente sous la forme d'un segment de droite, dont les extrémités correspondent à ce qu'on appelle des points cuspidaux.
Les figures 17 , 18 et 19 montrent comment on peut former un point cuspidal dans des régions à courbure positive, négative, ou nulle.
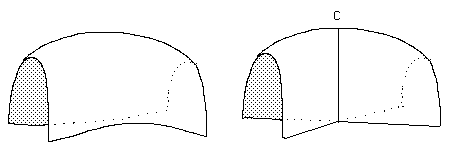
Fig.17 : Consitution d'un point cuspidal dans une région à courbure positive.
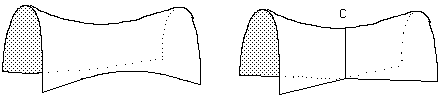
Fig.18 : Consitution d'un point cuspidal dans une région à courbure négative.
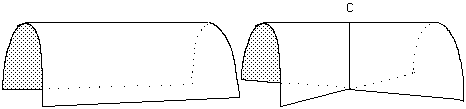
La figure 20 donne une représentation polyédrique du point cuspidal, dont nous allons nous servir par la suite.
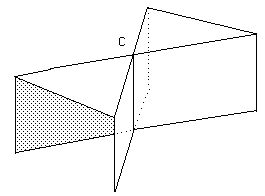
Figure 20 : Représentation polyédrique d'un point cuspidal
LA CROSS-CAP
Les figures 21a et 22b sont deux représentation polyédriques de la Cross-Cap, faciles à appréhender.
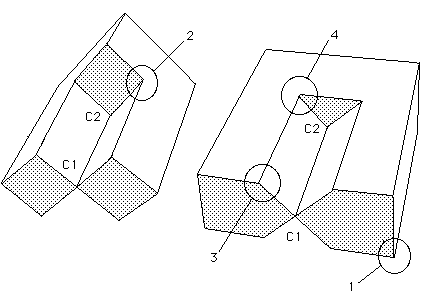
On sait que la courbure totale de la Cross-Cap est égale à 2 p. Comment la retrouver à partir d'une représentation polyédrique ?
La figure 22 permet de calculer la courbure concentrée dans un point cuspidal tel qu'il est présenté sur la figure 20.
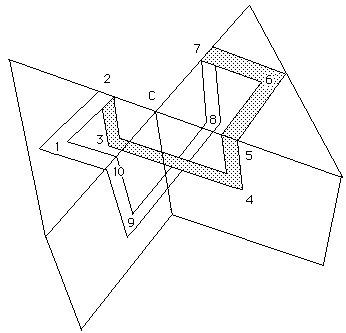
Le trajet figuré comporte six angles droits. Les cassures 2, 5 7 et 10 s'effectuent sur des arêtes et ne contiennent aucune courbure. Le trajet 1-2-3 s'effectue selon une géodésique de la surface. La courbure concentrée en ce point cuspidal particulier, où les nappes de croisent selon des angles droits, est égale à - p . Si on se réfèrent maintenant à la figure 21a et qu'on somme les courbures on trouve - 2 p . Il y a en effet :
Douze posicoins + p / 2
Quatre négacoins - p / 2
Deux points cuspidaux - p
Total 2 p
Les figures 21a et 21b montrent l'identité des deux points cuspidaux C1 et C2.
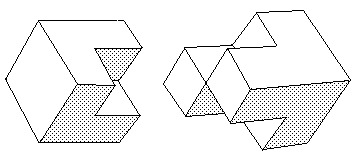
Fig.23 : Assemblage de deux Cross-Cap polyédriques.
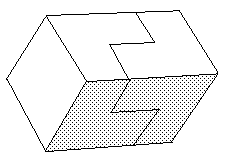
Après tout ceci nous sommes à même de bien comprendre la structure géométrique d'une Cross-Cap.
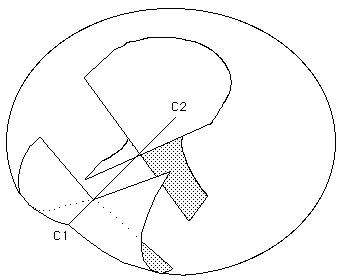
La même, sans ces détails :
PERMUTATION DES POINTS CUSPIDAUX D'UNE CROSS-CAP.
Il existe une symétrie entre ces deux points, qui n'apparaît pas de prime abord.
A parte :
Pour la petite histoire, je me suis posé ce problème après avoir participé à une colloque sur la psychanalyse Lacanienne, à Aix-en-Provence, sur invitation du comité d'organisation. On se demande ce que vient faire la psychanalyse Lacanienne dans un exposé de géométrie. Lacan, aujourd'hui décédé, a énoncé en son temps des théories assez impénétrables sur la structure de notre mental, qui serait organisé selon lui autour d'une "objet petit a", véritable "centre organisateur du langage". Pour Lacan, tout est langage (d'où sa phrase célèbre "l'acte sexuel n'existe pas"). Maintenant qu'il est mort, ses paroles se diluent un peu. Mais de son vivant, ses conférences à l'Ecole Normale Supérieure faisait courir le Tout-Paris intello. Les célébrités du cinéma aimaient à s'y faire voir. On se battait pour écouter ses propos abscons. Une des ses élèves, Jeanne Granier-Deferre, on pourrait dire de ses fidèles (le lacanisme était quasiment structuré comme une secte dont Lacan était le Gourou (dont il adoptait d'ailleurs le costume, voir quelques documents TV), avait publié un livre intitulé "la topologie selon Jacques Lacan" (...). Lacan avait recherché une surface unilatère pour modèliser la structure géométrico linguistique de notre "psyché". Pourquoi unulatère ? Pour figurer ce qu'il appelait l'énantiosémie, le double sens.
L'idée est loin d'être sotte. Témoin la phrase célèbre de Lacan :
où les cinq caractères constituant le mot homme n'ont pas le même sens dans les deux parties de la phrase. A gauche le mot homme se réfère au mâle de l'espèce humaine. A droite : le mot se réfère à ses attributs culturels (virilité, comportement, etc). Selon Lacan, notre langage utiliserait sans cesse le double sens, dans une dualité signifiant-signifié, ce qui n'est pas idiot non plus. On pourrait s'étendre sur les idées de feu Jacques, mais cela nous entraînerait trop loin. J'y consacrerai un dossier, que j'intitulerai probablement : "JPP chez Jacques Lacan", plein d'anecdotes savoureuses. En effet Lacan se manifesta immédiatement, lorsque parut en 79 notre article sur le retournement de la sphère, dans le numéro de janvier de Pour la Science. Il appela d'abord l'aveugle Morin, co-auteur qui, allergique à la psychanalyse (et à beaucoup d'autres choses du reste), l'envoya sur les roses. Par curiosité, je me rendis rue de Lille, àParis, chez Lacan, c'est à dire au sanctuaire de la secte. Récit de ces entrevues dans ce futur dossier.
Que Lacan se soit orienté vers de l'unilatère pour modèliser le langage, bon. Par exemple, si vous prenez le mot MOT et que vous considériez son image en miroir, son image énantiomorphe, cela donne TOM, ce qui n'a rien à voir. Mais les choses se compliquent avec "cet objet petit a" (selon Lacan un "phallus lingusitique"). Tout le langage de l'homme serait organisé autour de celui-ci. D'où une autre phrase célèbre de lacan :
Selon Lacan, l'homme ne serait qu'une machine à sécréter du langage, y compris lorsqu'il il fait l'amour, même en silence (un silence évidemment entièrement tissé de non-dits : pour Lacan le silence n'existe pas non plus...). Bref, l'homme ne ferait que circuler sur une "surface linguistique unilatère", entre signifiants et signifiés, dits et non-dits. Au centre de cet objet géométrico-linguistique, l'objet a, point du possible à penser mais de l'impossible à décrire : Dieu, ou "le père", peut-être, allez donc savoir. J'avoue que je n'ai jamais très bien compris. Mais après la mort de Lacan les psychanalystes Lacaniens, visiblement déboussolés par la disparition de leur gourou, tinrent à Aix un colloque, en avril 1978, et m'invitèrent en tant "qu'expert-géomètre". Au préalable il me passèrent le livre de Dame Granier-Deferre, cette "Topologie selon Jacques Lacan". Lacan avait choisi le point cuspidal central de la Cross-Cap (la seule surface unilatère qu'il savait manier) pour y situer son "objet petit a", y planter son "phallus linguistique". Tout de suite, j'imaginai une transformation permettant de "père-muter" les deux points cuspidaux. Ce fut un des thèmes de mon exposé, qui laissa la secte dans le plus complet désarroi (étant donnée la situation où ces 400 participants se trouvaient, au niveau psycho-analytique, je ne faisais qu'agraver les choses). Cette Cross-Cap, rebaptisée par Lacan le "fantasme fondamental", était donc dotée deux phallus lingusitiques au lieu d'un seul. J'essayai alors de sauver la situation en sortant une surface de Boy, fort à propos également unilatère, d'une caisse en carton, et en proposant à ces Lacaniens d'y planter leur "phallus linguistique", à l'unique pôle. Détails et suite de cette affaire dans ce futur dossier "JPP chez Lacan".
En refermant cette parenthèse, nous décrirons cette transformation que j'avais inventée à cette époque, permutant les deux points cuspidaux. Anecdotiquement, pour être mieux compris de mon auditoire, j'avais expliqué que l'opération d'invagination du point cuspidal C1 évoquait "un toucher vaginal chez une femelle de kangourou". En effet, les kangourous étant non placentaires, les trompes de Faloppe de la femelle débouchent directement dans l'appareil génital, exempt d'utérus, sauf erreur. Voir figure 19a et 19b.
Pour ce faire nous commençons par gonfler l'objet de manière à rassembler les deux points cuspidaux et le segment d'auto-intersection dans une région d'une sphère. Nous savons que nous pouvons retourner une sphère. La première version ayant été donnée par Anthony Phillips en 1967. Une seconde version fut ensuite inventée par le mathématicien Bernard Morin et publiée en 1979, aux CRAS ( illustrée par l'auteur ).
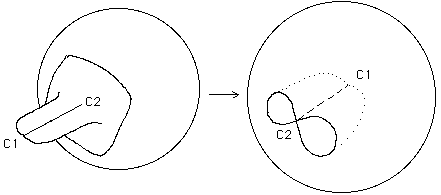
Le point cuspidal C1 est alors "à l'intérieur de la sphère". Il suffit de déformer l'objet selon les figures pour obtenir un résultat semblable à celui de la figure 15a. Mais les points cuspidaux ont alors été échangés.
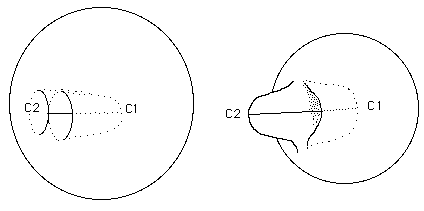
Figures 16a et 16b : On commence à déformer l'objet.
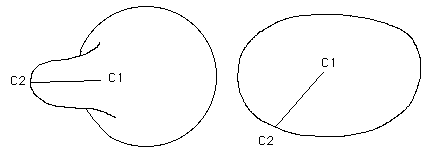
TRANSFORMATION DE LA CROSS-CAP EN SURFACE DE BOY VIA LA SURFACE ROMAINE DE STEINER
Reprenons la Cross-Cap. La figure 18b représente la surface "vue de profil". Ainsi on peut pincer le voisinage du segment d'auto-intersection entre deux doigts, comme indiqué
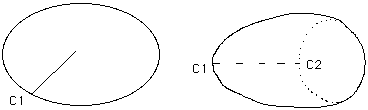
Figure 18a et 18b.
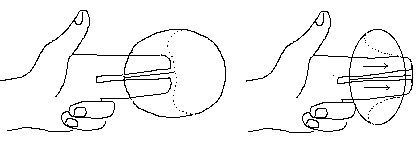
Figure 19a et 19b.
Le point cuspidal C2 traverse le "fond" de la Cross-Cap et apparaît "de l'autre côté". Au passage il se crée un point triple T, visible sur la vue 20a. En 20b on a représenté le voisinage de ce point triple.
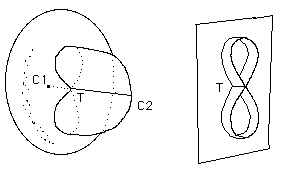
Détaillons ce modèle intermédiaire de la transformation. On a toujours le segment C1 C2 comme élément de l'ensemble d'auto-intersection. Mais le mouvement précédent a créé une courbe en huit qui est également partie intégrante de cet ensemble et qui passe par le point triple T.
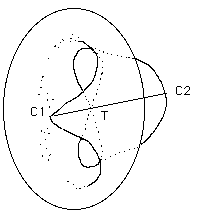
Figure 21 : le modèle intermédiaire
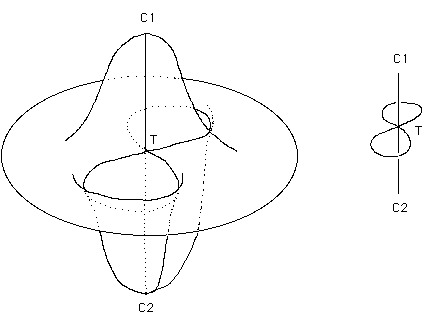
La figure 22 montre une autre vue de ce modèle intermédiaire et l'ensemble d'auto-intersection. Nous allons maintenant pincer la surface selon les flèches noires indiquées sur la figure 23.
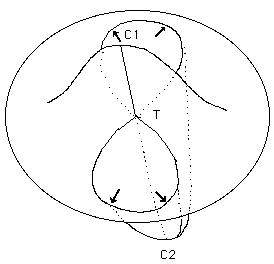
La disparition des passages tubulaires va donner naissance à deux nouvelles paires de points cuspidaux (C4 , C6 ) et ( C5, C4). Cet objet n'est autre qu la surface Romaine de Steiner.
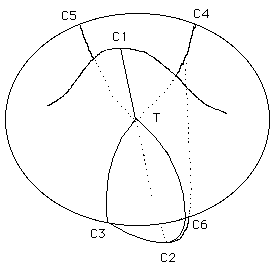
Les figures 25a et 25b sont des vues plus familières de la surface de Steiner, tandis que la figure 26 en est une représentation polyédrique.
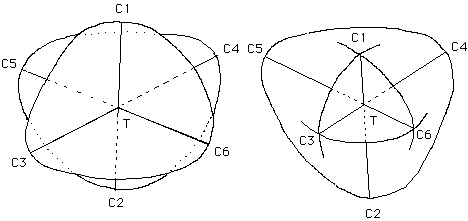
Figures 25a et 25b : Surface Romaine de Steiner
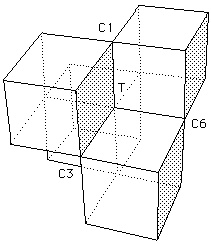
La figure 27 est une autre vue de cette représentation polyédrique qui montre qu'elle est constituée de quatre cubes accolés. L'ensemble d'auto-intersection est constitué de trois segments de droites qui concourent au point triple T. Aux extrémités de chacun de ces segments on trouve un point cuspidal.
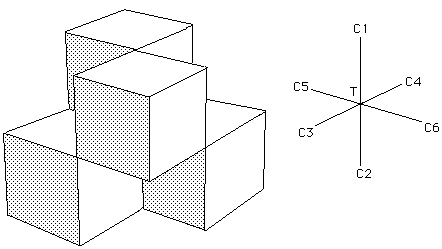
Il est maintenant possible d'envisager le passage à la surface de Boy. Pour ce faire nous allons faire confluer les points cuspidaux, deux à deux. C'est l'opération inverse de celle qui avait été utilisée pour passer de la figure 23 à la figure 24. On voit sur la figure 28a l'ordre dans lequel s'effectue cette confluence des points cuspidaux.
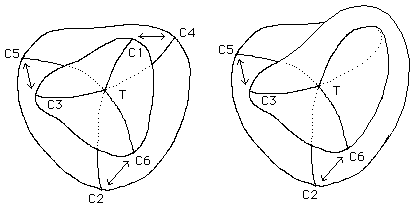
Sur la figure 28b deux des points cuspidaux ont déjà fusionné. L'opération est achevée dans les figures 29a et 19b où on reconnaît l'immersion du plan projectif, la surface de Boy.
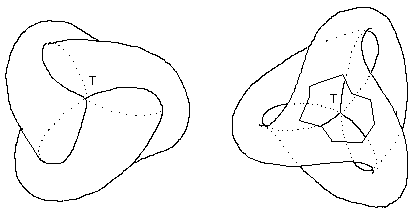
Une dernière remarque. Si au lieu de faire confluer les points :
on avait fait confluer les points :
on aurait obtenu l'image en miroir de la Boy. Ainsi l'objet intermédiaire qui est la surface de Steiner permet de transformer une surface de Boy droite en surface de Boy gauche, c'est à dire en son image énantiomorphe.
